2023-2024学年初中数学沪科版八年级下册18.2 第1课时 勾股定理的逆定理课件(共15张PPT)
文档属性
| 名称 | 2023-2024学年初中数学沪科版八年级下册18.2 第1课时 勾股定理的逆定理课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 637.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第十八章 勾股定理
18.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、学习目标
1.知道勾股定理的逆定理
2.能利用勾股定理的逆定理来判断一个三角形是不是直角三角形(难点)
二、新课导入
勾股定理 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
题设(条件):直角三角形的两直角边长为a,b,斜边长为c .
结论:a2+b2=c2.
问题 回忆勾股定理的内容.
形
数
三、概念剖析
逆向思考 提出问题
猜想 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是否是直角三角形?
三、概念剖析
证明猜想:
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
A
B
C
a
b
c
证明:作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
三、概念剖析
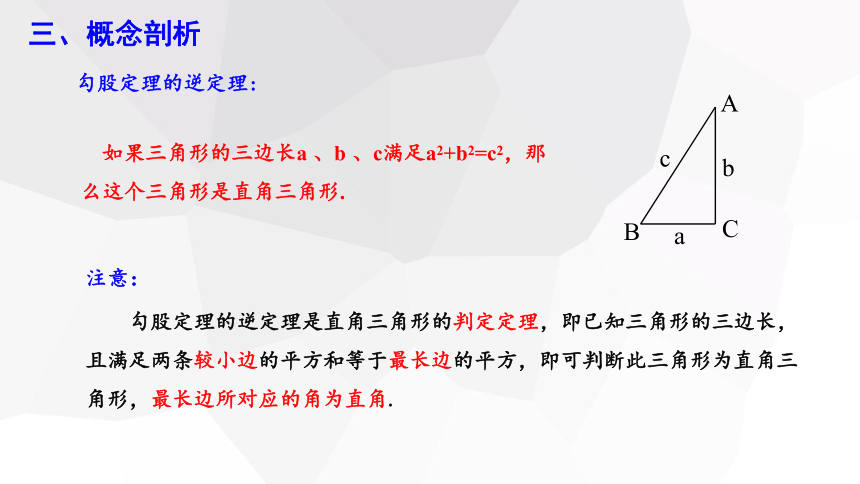
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,最长边所对应的角为直角.
注意:
四、典型例题
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15;
(2) a=13 b=14 c=15;
(3) a:b: c=3:4:5;
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方.
四、典型例题
(1) a=25 b=20 c=15;
解:(1)因为152+202=625,252=625,
(2) a=13 b=14 c=15;
(2)因为132+142=365,152=225,
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
所以152+202=252,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠A是直角.
所以132+142≠152,
不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
四、典型例题
(3) a:b: c=3:4:5;
(3)设a=3k,b=4k,c=5k,
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
因为(3k)2+(4k)2=25k2,
所以(3k)2+(4k)2=(5k)2,
(5k)2=25k2,
根据勾股定理的逆定理,这个三角形是直角三角形,
∠C是直角.
【当堂检测】
直角三角形
1.已知三角形的三边长分别为5cm、12cm、13cm,则这个三角形是 .
∴三边长分别为5cm、12cm、13cm的三角形是直角三角形.
∵52+122=169=132,
故答案是:直角三角形.
【当堂检测】
解:△ABC是直角三角形.
2.已知:在△ABC中,若△ABC的三边a,b,c满足 a:b: c=5:12:13,判断△ABC的形状.
∵a:b: c=5:12:13,
∴设a=5x,b=12x,c=13x.
则a2+b2=
=25x2+144x2
=169x2
∴△ABC的形状是直角三角形.
=(13x)2
= c2
(5x)2+(12x)2
四、典型例题
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
例2 如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE= CB,试判断AF与EF的位置关系,并说明理由.
【当堂检测】
3.一个三角形的三边长分别为13、5、12,则最长边上的高是( )
A.5 B.12 C. D.
D
故答案为D.
∴此三角形是直角三角形,设最长边上的高为h.
∵52+122=132,
S= ×5×12= ×13×h,解得:h= .
【当堂检测】
4.已知三角形ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm,求证:AB=AC
∴BD=CD=BC=5.
在△ABD中,
∵BD2+AD2=52+122=169,AB2=132=169,
∴BD2+AD2=AB2,
∴AD⊥BC.
在Rt△ADC中,AC2=AD2+CD2=122+52=169=132,
∴AB=AC.
证明:∵AD是BC边上的中线,
五、课堂总结
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
第十八章 勾股定理
18.2 勾股定理的逆定理
第1课时 勾股定理的逆定理
一、学习目标
1.知道勾股定理的逆定理
2.能利用勾股定理的逆定理来判断一个三角形是不是直角三角形(难点)
二、新课导入
勾股定理 如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
题设(条件):直角三角形的两直角边长为a,b,斜边长为c .
结论:a2+b2=c2.
问题 回忆勾股定理的内容.
形
数
三、概念剖析
逆向思考 提出问题
猜想 如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是否是直角三角形?
三、概念剖析
证明猜想:
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
A
B
C
a
b
c
证明:作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
三、概念剖析
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,最长边所对应的角为直角.
注意:
四、典型例题
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15;
(2) a=13 b=14 c=15;
(3) a:b: c=3:4:5;
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方.
四、典型例题
(1) a=25 b=20 c=15;
解:(1)因为152+202=625,252=625,
(2) a=13 b=14 c=15;
(2)因为132+142=365,152=225,
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
所以152+202=252,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠A是直角.
所以132+142≠152,
不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
四、典型例题
(3) a:b: c=3:4:5;
(3)设a=3k,b=4k,c=5k,
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
因为(3k)2+(4k)2=25k2,
所以(3k)2+(4k)2=(5k)2,
(5k)2=25k2,
根据勾股定理的逆定理,这个三角形是直角三角形,
∠C是直角.
【当堂检测】
直角三角形
1.已知三角形的三边长分别为5cm、12cm、13cm,则这个三角形是 .
∴三边长分别为5cm、12cm、13cm的三角形是直角三角形.
∵52+122=169=132,
故答案是:直角三角形.
【当堂检测】
解:△ABC是直角三角形.
2.已知:在△ABC中,若△ABC的三边a,b,c满足 a:b: c=5:12:13,判断△ABC的形状.
∵a:b: c=5:12:13,
∴设a=5x,b=12x,c=13x.
则a2+b2=
=25x2+144x2
=169x2
∴△ABC的形状是直角三角形.
=(13x)2
= c2
(5x)2+(12x)2
四、典型例题
解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
例2 如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE= CB,试判断AF与EF的位置关系,并说明理由.
【当堂检测】
3.一个三角形的三边长分别为13、5、12,则最长边上的高是( )
A.5 B.12 C. D.
D
故答案为D.
∴此三角形是直角三角形,设最长边上的高为h.
∵52+122=132,
S= ×5×12= ×13×h,解得:h= .
【当堂检测】
4.已知三角形ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm,求证:AB=AC
∴BD=CD=BC=5.
在△ABD中,
∵BD2+AD2=52+122=169,AB2=132=169,
∴BD2+AD2=AB2,
∴AD⊥BC.
在Rt△ADC中,AC2=AD2+CD2=122+52=169=132,
∴AB=AC.
证明:∵AD是BC边上的中线,
五、课堂总结
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
