19.1 多边形内角和 第2课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.1 多边形内角和 第2课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 929.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第十九章 四边形
19.1 多边形内角和
第2课时 多边形的外角和及三角形的稳定性
一、学习目标
1.了解三角形的稳定性和四边形的不稳定性
2.掌握多边形外角和定理及相关计算(重点)
3.知道正多边形的概念,并能计算正多边形的每个内角或外角的度数
二、新课导入
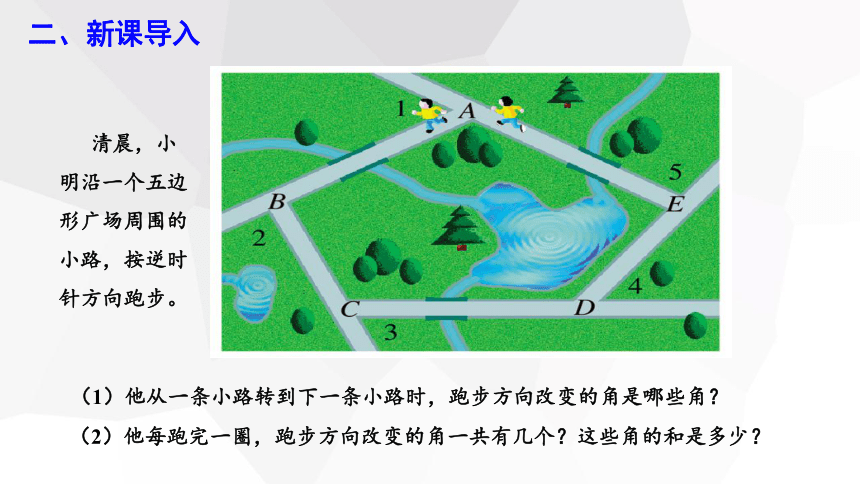
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)他从一条小路转到下一条小路时,跑步方向改变的角是哪些角?
(2)他每跑完一圈,跑步方向改变的角一共有几个?这些角的和是多少?
三、概念剖析
故四边形的外角和=4× 180°-(4-2) × 180°= 360°.
那么你能求出四边形的外角和吗?
思路:
知识点 一 多边形外角和
那么四边形的外角和就是4× 180°-(4-2) × 180°= 360°.
容易看出,4个外角+4个内角=4个平角,
而4个内角的和=(4-2) × 180 ° ,
解:因为4个外角+4个内角=4个平角,
而4个内角的和=(4-2) × 180 °,
三、概念剖析
类比四边形的外角和的求法,完成下面的表格:
三角形 四边形 五边形 六边形 n边形
内角和
外角和
从上面可以看出三边形、四边形、五边形、六边形的外角和为360°,那么n边形的外角和也是360°吗?
180°
360°
540°
720°
180°(n-2)
360°
360°
360°
360°
?
三、概念剖析
理论证明:
定理 n边形的外角和等于360°(n为不小于3的整数).
即:内角和+外角和=n×180°
而内角和=(n-2)× 180°
∴ 外角和=360°.
因为n边形的内角和与外角和之和构成n个平角.
∴(n-2)× 180°+外角和=n×180°
三、概念剖析
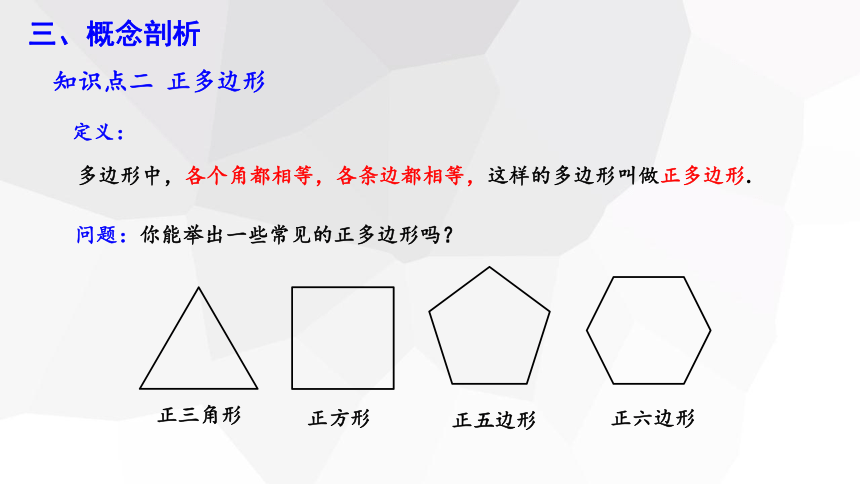
知识点二 正多边形
多边形中,各个角都相等,各条边都相等,这样的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
定义:
问题:你能举出一些常见的正多边形吗?
三、概念剖析
知识点三 三角形的稳定性和四边形的不稳定性
对比实验:(1)准备三根不同长度的小棒摆三角形.
(2)准备四根小棒(2长2短)摆四边形.看看你分别有多少种不同的摆法?
观察比较:三角形就摆出了一种.当三角形的三条边长度确定后,三角形的形状和大小也就被确定了,只是所摆的位置不同.
这个对比试验,告诉我们三角形稳定性的实质是指边长确定,则形状、大小唯一;而四边形不稳定性的实质是指四边形边长确定,其形状、大小不能完全确定.
而摆出的四边形有很多种,形状和大小也各不相同.
四、典型例题
提示:题目中隐含的条件是四边形外角和为360°.
例1.已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
解:设四边形的最小外角为x°,
则其他三个外角分别为2x°,3x°,4x°.
根据四边形外角和等于360°,
得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为36°,72°,108°,144°.
解得x°=36°,
【当堂检测】
1.五边形的外角和等于( )
A.180° B.540°
C.360° D.720°
C
【当堂检测】
2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
所以,这个多边形是八边形.
解:设这个多边形是n边形,
则它的内角和是(n-2)·180°,
外角和等于 360°.
根据题意,得 (n-2)·180°=3×360°.
解得n=8.
例2.正多边形的每个内角可能是:75°、90°或120°吗?说明理由.
解:75°不可能,90°或 120°可能.
理由:
与90°相邻的外角度数为90°,
而360不能被105整除.
故不可能.
与75°相邻的外角度数为105°,
360能被90整除.
故可能.
与120°相邻的外角度数为60°,
360能被60整除.
故可能.
四、典型例题
【当堂检测】
4.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.八边形 D.六边形
D
3.已知一个正多边形的每个外角等于36°,则这个正多边形是( )
A.正九边形 B.正十边形
C.正七边形 D.正八边形
B
5.求正六边形每个内角的度数和每个外角的度数.
解:正六边形的内角和为:
(6-2)×180°=720°,
正六边形的外角和为360°,
所以每个内角的度数为 720°÷ 6 = 120°,
每个外角的度数为 360°÷ 6 = 60°.
【当堂检测】
五、课堂总结
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多边形
内角= ,外角=
四边形
具有不稳定性
多边形的外角和及三角形的稳定性
第十九章 四边形
19.1 多边形内角和
第2课时 多边形的外角和及三角形的稳定性
一、学习目标
1.了解三角形的稳定性和四边形的不稳定性
2.掌握多边形外角和定理及相关计算(重点)
3.知道正多边形的概念,并能计算正多边形的每个内角或外角的度数
二、新课导入
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)他从一条小路转到下一条小路时,跑步方向改变的角是哪些角?
(2)他每跑完一圈,跑步方向改变的角一共有几个?这些角的和是多少?
三、概念剖析
故四边形的外角和=4× 180°-(4-2) × 180°= 360°.
那么你能求出四边形的外角和吗?
思路:
知识点 一 多边形外角和
那么四边形的外角和就是4× 180°-(4-2) × 180°= 360°.
容易看出,4个外角+4个内角=4个平角,
而4个内角的和=(4-2) × 180 ° ,
解:因为4个外角+4个内角=4个平角,
而4个内角的和=(4-2) × 180 °,
三、概念剖析
类比四边形的外角和的求法,完成下面的表格:
三角形 四边形 五边形 六边形 n边形
内角和
外角和
从上面可以看出三边形、四边形、五边形、六边形的外角和为360°,那么n边形的外角和也是360°吗?
180°
360°
540°
720°
180°(n-2)
360°
360°
360°
360°
?
三、概念剖析
理论证明:
定理 n边形的外角和等于360°(n为不小于3的整数).
即:内角和+外角和=n×180°
而内角和=(n-2)× 180°
∴ 外角和=360°.
因为n边形的内角和与外角和之和构成n个平角.
∴(n-2)× 180°+外角和=n×180°
三、概念剖析
知识点二 正多边形
多边形中,各个角都相等,各条边都相等,这样的多边形叫做正多边形.
正三角形
正方形
正五边形
正六边形
定义:
问题:你能举出一些常见的正多边形吗?
三、概念剖析
知识点三 三角形的稳定性和四边形的不稳定性
对比实验:(1)准备三根不同长度的小棒摆三角形.
(2)准备四根小棒(2长2短)摆四边形.看看你分别有多少种不同的摆法?
观察比较:三角形就摆出了一种.当三角形的三条边长度确定后,三角形的形状和大小也就被确定了,只是所摆的位置不同.
这个对比试验,告诉我们三角形稳定性的实质是指边长确定,则形状、大小唯一;而四边形不稳定性的实质是指四边形边长确定,其形状、大小不能完全确定.
而摆出的四边形有很多种,形状和大小也各不相同.
四、典型例题
提示:题目中隐含的条件是四边形外角和为360°.
例1.已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
解:设四边形的最小外角为x°,
则其他三个外角分别为2x°,3x°,4x°.
根据四边形外角和等于360°,
得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为36°,72°,108°,144°.
解得x°=36°,
【当堂检测】
1.五边形的外角和等于( )
A.180° B.540°
C.360° D.720°
C
【当堂检测】
2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
所以,这个多边形是八边形.
解:设这个多边形是n边形,
则它的内角和是(n-2)·180°,
外角和等于 360°.
根据题意,得 (n-2)·180°=3×360°.
解得n=8.
例2.正多边形的每个内角可能是:75°、90°或120°吗?说明理由.
解:75°不可能,90°或 120°可能.
理由:
与90°相邻的外角度数为90°,
而360不能被105整除.
故不可能.
与75°相邻的外角度数为105°,
360能被90整除.
故可能.
与120°相邻的外角度数为60°,
360能被60整除.
故可能.
四、典型例题
【当堂检测】
4.一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.八边形 D.六边形
D
3.已知一个正多边形的每个外角等于36°,则这个正多边形是( )
A.正九边形 B.正十边形
C.正七边形 D.正八边形
B
5.求正六边形每个内角的度数和每个外角的度数.
解:正六边形的内角和为:
(6-2)×180°=720°,
正六边形的外角和为360°,
所以每个内角的度数为 720°÷ 6 = 120°,
每个外角的度数为 360°÷ 6 = 60°.
【当堂检测】
五、课堂总结
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多边形
内角= ,外角=
四边形
具有不稳定性
多边形的外角和及三角形的稳定性
