17.2.2 配方法 课件 14张PPT 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 17.2.2 配方法 课件 14张PPT 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:03:12 | ||
图片预览






文档简介
(共14张PPT)
17.2 一元二次方程的解法
2.配方法
第十七章 一元二次方程
一、学习目标
1.知道配方法的概念,掌握配方法的步骤
2.能运用配方法解一元二次方程
二、新课导入
1.用直接开方法解下列方程:
(1)9x2=1 (2)(x-2)2=2
2.下列方程能用直接开方法来解吗?
(1)x2+6x+9=5
(2)x2+6x+4=0
三、典型例题
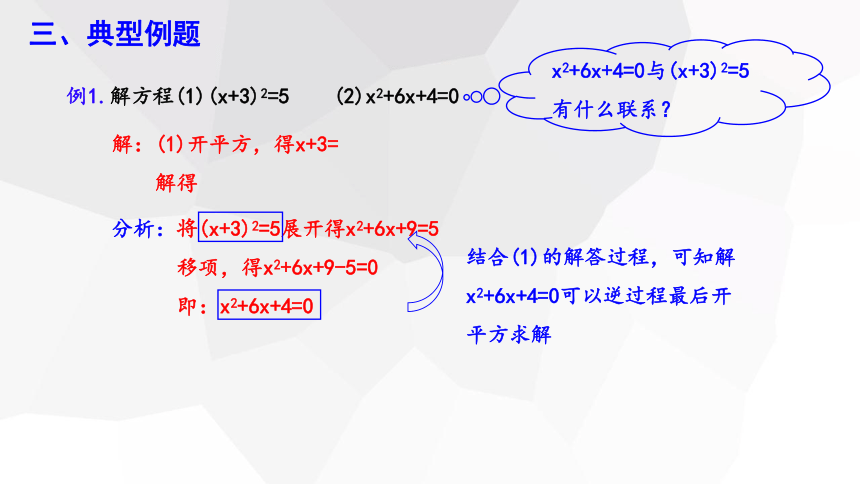
例1.解方程(1)(x+3)2=5 (2)x2+6x+4=0
解:(1)开平方,得x+3=
解得
结合(1)的解答过程,可知解x2+6x+4=0可以逆过程最后开平方求解
x2+6x+4=0与(x+3)2=5有什么联系?
分析:将(x+3)2=5展开得x2+6x+9=5
移项,得x2+6x+9-5=0
即:x2+6x+4=0
解方程(2)x2+6x+4=0
(2)x2+6x+4=0
移项,得x2+6x=-4
两边同时加上9,得x2+6x+32=-4+32
即(x+3)2=5
开平方,得x+3=
解得
配方
三、典型例题
注意:配方时, 等式两边同时加上的是一次项系数一半的平方.
议一议:说出解一般二次项系数为1(如x2+6x+4=0)的一元二次方程的基本思路是什么?
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为一元一次方程求解.
对一个一元二次方程进行配方,使它出现完全平方式后,再直接开平方求解的方法,叫做配方法.
三、典型例题
【当堂检测】
1.如果x2-8x+m=0可以通过配方写成(x-n)2=6的形式,那么m、n的值分别为( )
A.10,-4 B.-10,4
C.10,4 D.-10,-4
C
提示:将(x-n)2=6展开对比系数得出结果.
【当堂检测】
2.解下列方程:
(1)x2+2x=3 (2)x2-4x-7=0
解:(1)配方,得x2+2x+1=3+1
即(x+1)2=4
开平方,得x+1=±2
解得x1=1,x2=-3
(2)移项,得x2-4x=7
配方,得x2-4x+4=7+4
即(x-2)2=11
开平方,得x-2=
解得
例2.解方程(1)2x2+x-6=0
解:(1)方程两边同时除以2,得
移项,得
配方,得
即
开平方,得
解得
三、典型例题
分析:不可直接开方,将系数化为1,构造出(x+n)2=p来解题
例2.解方程(2)3x2-6x=-4
(2)方程两边同时除以3,得
配方,得
即
∵一个数的平方大于等于0
∴方程不可以开平方
即方程没有实数根
三、典型例题
想一想用配方法解一元二次方程有哪些步骤
用配方法解一元二次方程的一般步骤:
(1)一化:化二次项系数为1(方程两边都除以二次项系数);
(2)移项:把常数项移到方程的右边;
(3)配方:两边都加上一次项系数一半的平方,使左边变为完全平方式;
(4)若右边是非负数,则直接用开平方法求解;若右边是负数,则方程无解.
三、典型例题
【当堂检测】
3.用配方法解方程2x2-8x-3=0时,原方程可变形为( )
A.(x-2)2= B.(x-2)2=
C.(x+2)2=7 D.(x+4)2=7
B
【当堂检测】
4.解下列方程:
(1)2x2-4x+1=0 (2)
解:(1)移项,得2x2-4x=-1
方程两边同时除以2,得
配方,得
即
开平方,得
(2)方程两边同时乘以2,得
配方,得
即
开平方,得
四、课堂总结
1.对一个一元二次方程进行配方,使它出现完全平方式后,再直接开平方求解的方法,叫做配方法.
2.用配方法解一元二次方程的一般步骤是:
(1)一化;(2)移项;(3)配方;(4)开方求解
3.在配方过程中需要注意:两边同时加上一次项系数的一半的平方.
4.配方后形如(x+n)2=p,当p<0时,方程无解.
17.2 一元二次方程的解法
2.配方法
第十七章 一元二次方程
一、学习目标
1.知道配方法的概念,掌握配方法的步骤
2.能运用配方法解一元二次方程
二、新课导入
1.用直接开方法解下列方程:
(1)9x2=1 (2)(x-2)2=2
2.下列方程能用直接开方法来解吗?
(1)x2+6x+9=5
(2)x2+6x+4=0
三、典型例题
例1.解方程(1)(x+3)2=5 (2)x2+6x+4=0
解:(1)开平方,得x+3=
解得
结合(1)的解答过程,可知解x2+6x+4=0可以逆过程最后开平方求解
x2+6x+4=0与(x+3)2=5有什么联系?
分析:将(x+3)2=5展开得x2+6x+9=5
移项,得x2+6x+9-5=0
即:x2+6x+4=0
解方程(2)x2+6x+4=0
(2)x2+6x+4=0
移项,得x2+6x=-4
两边同时加上9,得x2+6x+32=-4+32
即(x+3)2=5
开平方,得x+3=
解得
配方
三、典型例题
注意:配方时, 等式两边同时加上的是一次项系数一半的平方.
议一议:说出解一般二次项系数为1(如x2+6x+4=0)的一元二次方程的基本思路是什么?
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为一元一次方程求解.
对一个一元二次方程进行配方,使它出现完全平方式后,再直接开平方求解的方法,叫做配方法.
三、典型例题
【当堂检测】
1.如果x2-8x+m=0可以通过配方写成(x-n)2=6的形式,那么m、n的值分别为( )
A.10,-4 B.-10,4
C.10,4 D.-10,-4
C
提示:将(x-n)2=6展开对比系数得出结果.
【当堂检测】
2.解下列方程:
(1)x2+2x=3 (2)x2-4x-7=0
解:(1)配方,得x2+2x+1=3+1
即(x+1)2=4
开平方,得x+1=±2
解得x1=1,x2=-3
(2)移项,得x2-4x=7
配方,得x2-4x+4=7+4
即(x-2)2=11
开平方,得x-2=
解得
例2.解方程(1)2x2+x-6=0
解:(1)方程两边同时除以2,得
移项,得
配方,得
即
开平方,得
解得
三、典型例题
分析:不可直接开方,将系数化为1,构造出(x+n)2=p来解题
例2.解方程(2)3x2-6x=-4
(2)方程两边同时除以3,得
配方,得
即
∵一个数的平方大于等于0
∴方程不可以开平方
即方程没有实数根
三、典型例题
想一想用配方法解一元二次方程有哪些步骤
用配方法解一元二次方程的一般步骤:
(1)一化:化二次项系数为1(方程两边都除以二次项系数);
(2)移项:把常数项移到方程的右边;
(3)配方:两边都加上一次项系数一半的平方,使左边变为完全平方式;
(4)若右边是非负数,则直接用开平方法求解;若右边是负数,则方程无解.
三、典型例题
【当堂检测】
3.用配方法解方程2x2-8x-3=0时,原方程可变形为( )
A.(x-2)2= B.(x-2)2=
C.(x+2)2=7 D.(x+4)2=7
B
【当堂检测】
4.解下列方程:
(1)2x2-4x+1=0 (2)
解:(1)移项,得2x2-4x=-1
方程两边同时除以2,得
配方,得
即
开平方,得
(2)方程两边同时乘以2,得
配方,得
即
开平方,得
四、课堂总结
1.对一个一元二次方程进行配方,使它出现完全平方式后,再直接开平方求解的方法,叫做配方法.
2.用配方法解一元二次方程的一般步骤是:
(1)一化;(2)移项;(3)配方;(4)开方求解
3.在配方过程中需要注意:两边同时加上一次项系数的一半的平方.
4.配方后形如(x+n)2=p,当p<0时,方程无解.
