19.2 平行四边形 第3课时 课件(共14张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.2 平行四边形 第3课时 课件(共14张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 534.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:53:42 | ||
图片预览






文档简介
(共14张PPT)
第十九章 四边形
19.2 平行四边形
第3课时
1.掌握平行四边形的判定定理1
2.能利用判定方法解决相关几何问题
一、学习目标
二、新课导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
思考:在数学中,我们要怎么确保一个四边形是否是平行四边形呢?
三、概念剖析
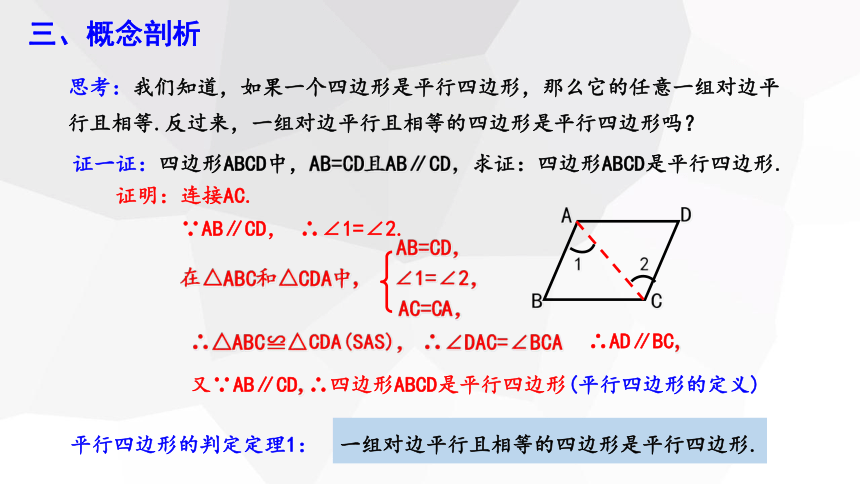
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
证一证:四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴∠DAC=∠BCA
∴四边形ABCD是平行四边形(平行四边形的定义)
∴AD∥BC,
A
B
C
D
AB=CD,
AC=CA,
∠1=∠2,
2
1
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
又∵AB∥CD,
三、概念剖析
归纳总结:
平行四边形判定方法:(定义法)两组对边分别平行的四边形是平行四边形;
(定理1)一组对边平行且相等的四边形是平行四边形.
B
D
C
A
∵AB=CD,AB∥CD
∴四边形ABCD是平行四边形.
定理1的几何语言:
例1.如图, ABCD中,AC为对角线,G为CD的中点,连接AG并廷长交BC的延长线于点F,连接DF.求证:四边形ACFD为平行四边形.
四、典型例题
证明:∵四边形ABCD是平行四边形
∴AD∥BF
∵G是CD的中点
∵在△ADG和△FCG中,
∴△ADG≌△FCG(ASA)
∴AD=CF
∴四边形ACFD是平行四边形.
∴∠ADG=∠FCG
∴DG=CG
∠ADG=∠FCG
∠AGD=∠CGF
DG=CG
又∵AD∥CF
【当堂检测】
1.已知四边形ABCD,给出下列条件:①AB∥CD;②BC∥AD;③AB=CD;④∠A=∠C;从中任取两个条件,可以得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种 B.4种 C.3种 D.2种
B
平行四边形判定方法:定义法:两组对边分别平行;
判定定理1:一组对边平行且相等.
注意:角变化可以转化为线段平行.
【当堂检测】
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠DBE=∠BDE,
∵BE=AF,
∵DE∥AF,
∴四边形ADEF是平行四边形.
∴∠ABD=∠BDE,
∴BE=DE;
∴AF=DE;
例2.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.
(1)求证:AD与BE互相平分.
(2)若AD⊥BE,DE=10,AD=12,DF= ,求BF的长.
分析:(1)连接BD,AE.根据平行线的性质得到∠ABC=∠DEF,∠ACB=∠DFE.
根据全等三角形的性质得到AB=DE,根据平行四边形的判定和性质即可得到结论.
(2)利用(1)及勾股定理可求出OB,OF的长,即可得到BF的值.
四、典型例题
例2.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.(1)求证:AD与BE互相平分.
证明:连接 BD,AE
∵AB∥ED,
∵AC∥FD,
∵FB=CE,BC=FB+OF,EF=CE+OC
∴BC=EF
在△ACB 和△DFE中,
∴∠ABC=∠DEF
∴∠ACB=∠DFE
∴△ACB≌△DFE(ASA)
∴AB=DE
∵AB∥ED
∴四边形ABDE是平行四边形
∴AD与BE互相平分
四、典型例题
(2)若AD⊥BE,DE=10,AD=12,DF= ,求BF的长.
解:由(1)可知四边形ABDE是平行四边形
∴AB=DE=10,AO=DO=6
∵AD⊥BE
∴在△ABO中有AB2=AO2+OB2
在△FOD中有DF2=DO2+OF2
即102=62+OB2,
∴OB=8,OF=2
∴BF=OB-OF=8-2=6
四、典型例题
方法归纳:根据题目所求找出所在平行四边形,根据平行四边形性质解题.
【当堂检测】
3.如图,平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F,连接AF、CE.求证:AF=CE.
证明:∵AE⊥AD交BD于点E,CF⊥BC交BD于点F,
∴∠DAE=∠BCF=90°,
∵平行四边形ABCD中,AD∥BC,
∴∠ADE=∠CBF,
又∵平行四边形ABCD中,AD=BC,
∴△ADE≌△CBF(ASA),
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE.
【当堂检测】
4.如图,在△ABC中,已知∠ACB=90°,D是BC的中点,CE=BE=5,BC=8,CE∥AD,求AC的长.
解:∵D是BC的中点,CE=BE
∴CD⊥BC
∵∠ACB=90°
∴DE∥AC
∴四边形ADEC是平行四边形
∴AC=DE
∵D是BC的中点
∴AC⊥BC
又∵CE∥AD
Rt△CDE中有CE2=CD2+DE2
即52=42+DE2
∴DE=3
∴AC=DE=3
∴CD= BC=4
五、课堂总结
1.平行四边形的判定方法:
(1)两组对边分别平行的四边形是平行四边形(定义法);
(2)一组对边平行且相等的四边形是平行四边形(定理1).
2.解决相关几何问题时,求证所在四边形是平行四边形,根据平行四边形的性质解题.
第十九章 四边形
19.2 平行四边形
第3课时
1.掌握平行四边形的判定定理1
2.能利用判定方法解决相关几何问题
一、学习目标
二、新课导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
思考:在数学中,我们要怎么确保一个四边形是否是平行四边形呢?
三、概念剖析
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
证一证:四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴∠DAC=∠BCA
∴四边形ABCD是平行四边形(平行四边形的定义)
∴AD∥BC,
A
B
C
D
AB=CD,
AC=CA,
∠1=∠2,
2
1
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
又∵AB∥CD,
三、概念剖析
归纳总结:
平行四边形判定方法:(定义法)两组对边分别平行的四边形是平行四边形;
(定理1)一组对边平行且相等的四边形是平行四边形.
B
D
C
A
∵AB=CD,AB∥CD
∴四边形ABCD是平行四边形.
定理1的几何语言:
例1.如图, ABCD中,AC为对角线,G为CD的中点,连接AG并廷长交BC的延长线于点F,连接DF.求证:四边形ACFD为平行四边形.
四、典型例题
证明:∵四边形ABCD是平行四边形
∴AD∥BF
∵G是CD的中点
∵在△ADG和△FCG中,
∴△ADG≌△FCG(ASA)
∴AD=CF
∴四边形ACFD是平行四边形.
∴∠ADG=∠FCG
∴DG=CG
∠ADG=∠FCG
∠AGD=∠CGF
DG=CG
又∵AD∥CF
【当堂检测】
1.已知四边形ABCD,给出下列条件:①AB∥CD;②BC∥AD;③AB=CD;④∠A=∠C;从中任取两个条件,可以得出四边形ABCD是平行四边形这一结论的情况有( )
A.5种 B.4种 C.3种 D.2种
B
平行四边形判定方法:定义法:两组对边分别平行;
判定定理1:一组对边平行且相等.
注意:角变化可以转化为线段平行.
【当堂检测】
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠DBE=∠BDE,
∵BE=AF,
∵DE∥AF,
∴四边形ADEF是平行四边形.
∴∠ABD=∠BDE,
∴BE=DE;
∴AF=DE;
例2.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.
(1)求证:AD与BE互相平分.
(2)若AD⊥BE,DE=10,AD=12,DF= ,求BF的长.
分析:(1)连接BD,AE.根据平行线的性质得到∠ABC=∠DEF,∠ACB=∠DFE.
根据全等三角形的性质得到AB=DE,根据平行四边形的判定和性质即可得到结论.
(2)利用(1)及勾股定理可求出OB,OF的长,即可得到BF的值.
四、典型例题
例2.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,BF=CE,AD交BE于点O.(1)求证:AD与BE互相平分.
证明:连接 BD,AE
∵AB∥ED,
∵AC∥FD,
∵FB=CE,BC=FB+OF,EF=CE+OC
∴BC=EF
在△ACB 和△DFE中,
∴∠ABC=∠DEF
∴∠ACB=∠DFE
∴△ACB≌△DFE(ASA)
∴AB=DE
∵AB∥ED
∴四边形ABDE是平行四边形
∴AD与BE互相平分
四、典型例题
(2)若AD⊥BE,DE=10,AD=12,DF= ,求BF的长.
解:由(1)可知四边形ABDE是平行四边形
∴AB=DE=10,AO=DO=6
∵AD⊥BE
∴在△ABO中有AB2=AO2+OB2
在△FOD中有DF2=DO2+OF2
即102=62+OB2,
∴OB=8,OF=2
∴BF=OB-OF=8-2=6
四、典型例题
方法归纳:根据题目所求找出所在平行四边形,根据平行四边形性质解题.
【当堂检测】
3.如图,平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F,连接AF、CE.求证:AF=CE.
证明:∵AE⊥AD交BD于点E,CF⊥BC交BD于点F,
∴∠DAE=∠BCF=90°,
∵平行四边形ABCD中,AD∥BC,
∴∠ADE=∠CBF,
又∵平行四边形ABCD中,AD=BC,
∴△ADE≌△CBF(ASA),
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE.
【当堂检测】
4.如图,在△ABC中,已知∠ACB=90°,D是BC的中点,CE=BE=5,BC=8,CE∥AD,求AC的长.
解:∵D是BC的中点,CE=BE
∴CD⊥BC
∵∠ACB=90°
∴DE∥AC
∴四边形ADEC是平行四边形
∴AC=DE
∵D是BC的中点
∴AC⊥BC
又∵CE∥AD
Rt△CDE中有CE2=CD2+DE2
即52=42+DE2
∴DE=3
∴AC=DE=3
∴CD= BC=4
五、课堂总结
1.平行四边形的判定方法:
(1)两组对边分别平行的四边形是平行四边形(定义法);
(2)一组对边平行且相等的四边形是平行四边形(定理1).
2.解决相关几何问题时,求证所在四边形是平行四边形,根据平行四边形的性质解题.
