19.3.1 矩形 第2课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.3.1 矩形 第2课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:56:36 | ||
图片预览





文档简介
(共15张PPT)
第十九章 四边形
19.3.1 矩形
第2课时
1.理解并掌握矩形的判定方法
2.能应用矩形定义、判定等知识解决相关问题
一、学习目标
二、新课导入
1.矩形的定义是什么?
怎样判断一个四边形是否是矩形呢
有一个角是直角的平行四边形叫做矩形.
2.矩形的有哪些性质?
①对边平行且相等;
②四个角都是直角;
③对角线互相平分且相等.
三、概念剖析
思考:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
证一证:已知:如图,在□ABCD中,AC、BD是它的两条对角线, AC=BD.
求证:□ABCD是矩形.
三、概念剖析
证明:在□ABCD中,由于AB=DC,AC=DB,BC=CB,
因此 △ABC≌△DCB. (SSS)
从而 ∠ABC=∠DCB.
又 ∠ABC +∠DCB =180°,
于是 ∠ABC=90°.
所以 □ABCD是矩形.
矩形的判定定理1:
对角线相等的平行四边形是矩形.
三、概念剖析
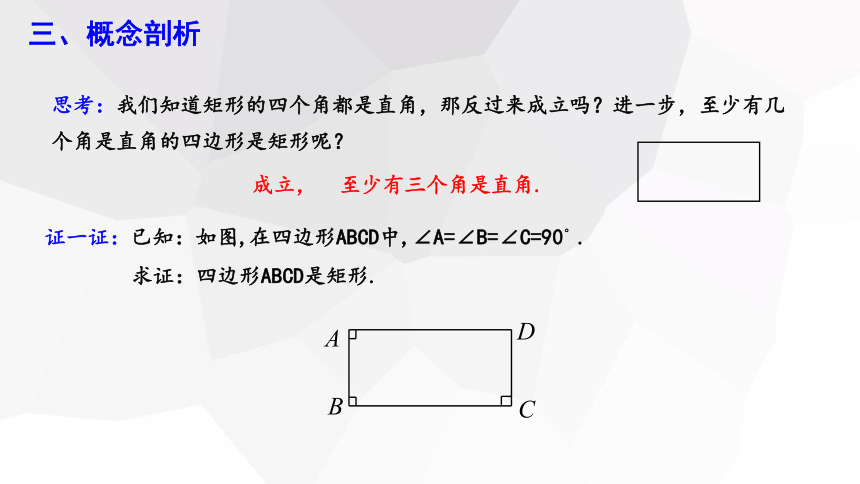
思考:我们知道矩形的四个角都是直角,那反过来成立吗?进一步,至少有几个角是直角的四边形是矩形呢?
证一证:已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
成立,
至少有三个角是直角.
三、概念剖析
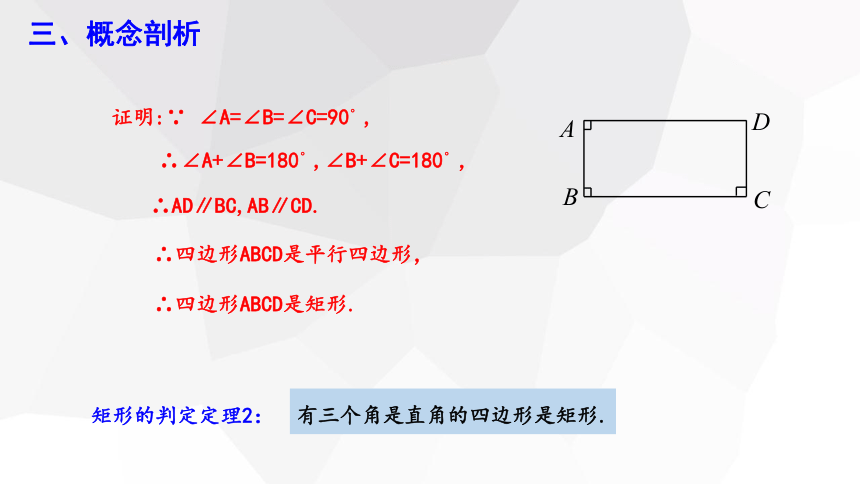
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:
有三个角是直角的四边形是矩形.
A
B
C
D
三、概念剖析
矩形的判定定理:
对角线相等的平行四边形是矩形;
有三个角是直角的四边形是矩形;
有一个角是直角的平行四边形是矩形.(定义)
例1.如图,在 ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
求证:四边形BECD是矩形.
证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵∠ABD=90°,
∴∠DBE=90°.
∴四边形BECD是矩形.
四、典型例题
要获取足够证明一个四边形为矩形的条件,往往需要结合图形中的其他条件,进行相关的推理.应根据已知条件,猜测最可能获取到的条件,从而选择合适的判定方法.
方法归纳:
四、典型例题
【当堂检测】
1.如图,为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理:
.
对角线相等的平行四边形是矩形,矩形的四个角都是直角
提示:(1)有三个角是直角的四边形是矩形;
(2)有个角是直角的平行四边形是矩形;
(3)对角线相等的平行四边形是矩形.
2.如图 ABCD中, ∠1=∠2中.此时四边形ABCD是矩形吗?为什么?
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2,
∴AO=BO,
【当堂检测】
∴AC=BD,
∴四边形ABCD是矩形.
A
B
C
D
O
1
2
例2.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.连结DE,交AB与点O,若AE=4,AO=2.5,求△ABC的面积.
解:∵AE∥BC,BE∥AD,
∴四边形ADBE是平行四边形
∵AB=AC,AD是BC边的中线
∴AD⊥BC,BC=2BD
即∠ADB=90°
∴四边形ADBE为矩形
∴DE=AB=2AO=2×2.5=5,BD=AE=4
∴BC=2BD=8
Rt△ADE中,DE2=AD2+AE2
即52=AD2+42
∴AD=3
∴S△ABC=
四、典型例题
3.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连结AC.若AC平分∠DAB,AB=5,EC=2,求AE的长.
解:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
∴AE⊥BC
∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
【当堂检测】
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=BC-CE=3.
Rt△ABE中,AB2=BE2+AE2
即52=32+AE2
∴AE=4
五、课堂总结
2.矩形的判定定理:
对角线相等的平行四边形是矩形;
有三个角是直角的四边形是矩形.
1.矩形的定义:
有一个角是直角的平行四边形是矩形.
第十九章 四边形
19.3.1 矩形
第2课时
1.理解并掌握矩形的判定方法
2.能应用矩形定义、判定等知识解决相关问题
一、学习目标
二、新课导入
1.矩形的定义是什么?
怎样判断一个四边形是否是矩形呢
有一个角是直角的平行四边形叫做矩形.
2.矩形的有哪些性质?
①对边平行且相等;
②四个角都是直角;
③对角线互相平分且相等.
三、概念剖析
思考:我们知道,矩形的对角线相等.反过来,对角线相等的平行四边形是矩形吗?
证一证:已知:如图,在□ABCD中,AC、BD是它的两条对角线, AC=BD.
求证:□ABCD是矩形.
三、概念剖析
证明:在□ABCD中,由于AB=DC,AC=DB,BC=CB,
因此 △ABC≌△DCB. (SSS)
从而 ∠ABC=∠DCB.
又 ∠ABC +∠DCB =180°,
于是 ∠ABC=90°.
所以 □ABCD是矩形.
矩形的判定定理1:
对角线相等的平行四边形是矩形.
三、概念剖析
思考:我们知道矩形的四个角都是直角,那反过来成立吗?进一步,至少有几个角是直角的四边形是矩形呢?
证一证:已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
成立,
至少有三个角是直角.
三、概念剖析
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理2:
有三个角是直角的四边形是矩形.
A
B
C
D
三、概念剖析
矩形的判定定理:
对角线相等的平行四边形是矩形;
有三个角是直角的四边形是矩形;
有一个角是直角的平行四边形是矩形.(定义)
例1.如图,在 ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
求证:四边形BECD是矩形.
证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵∠ABD=90°,
∴∠DBE=90°.
∴四边形BECD是矩形.
四、典型例题
要获取足够证明一个四边形为矩形的条件,往往需要结合图形中的其他条件,进行相关的推理.应根据已知条件,猜测最可能获取到的条件,从而选择合适的判定方法.
方法归纳:
四、典型例题
【当堂检测】
1.如图,为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理:
.
对角线相等的平行四边形是矩形,矩形的四个角都是直角
提示:(1)有三个角是直角的四边形是矩形;
(2)有个角是直角的平行四边形是矩形;
(3)对角线相等的平行四边形是矩形.
2.如图 ABCD中, ∠1=∠2中.此时四边形ABCD是矩形吗?为什么?
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2,
∴AO=BO,
【当堂检测】
∴AC=BD,
∴四边形ABCD是矩形.
A
B
C
D
O
1
2
例2.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.连结DE,交AB与点O,若AE=4,AO=2.5,求△ABC的面积.
解:∵AE∥BC,BE∥AD,
∴四边形ADBE是平行四边形
∵AB=AC,AD是BC边的中线
∴AD⊥BC,BC=2BD
即∠ADB=90°
∴四边形ADBE为矩形
∴DE=AB=2AO=2×2.5=5,BD=AE=4
∴BC=2BD=8
Rt△ADE中,DE2=AD2+AE2
即52=AD2+42
∴AD=3
∴S△ABC=
四、典型例题
3.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连结AC.若AC平分∠DAB,AB=5,EC=2,求AE的长.
解:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
∴AE⊥BC
∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
【当堂检测】
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=BC-CE=3.
Rt△ABE中,AB2=BE2+AE2
即52=32+AE2
∴AE=4
五、课堂总结
2.矩形的判定定理:
对角线相等的平行四边形是矩形;
有三个角是直角的四边形是矩形.
1.矩形的定义:
有一个角是直角的平行四边形是矩形.
