19.3.2 菱形 第1课时 课件 (共16张PPT)2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.3.2 菱形 第1课时 课件 (共16张PPT)2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 558.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:56:07 | ||
图片预览




文档简介
(共16张PPT)
第十九章 四边形
19.3 矩形、菱形、正方形
第1课时
1.了解菱形的概念及其与平行四边形的关系
2.探索并证明菱形的性质定理
3.应用菱形的性质定理解决相关计算或证明问题
一、学习目标
欣赏下面图片,图片中框出的图形是你熟悉的吗?
二、新课导入
(一)菱形的概念
定义:有一组邻边相等的平行四边形叫做菱形.
注意:①菱形是特殊的平行四边形.
②平行四边形不一定是菱形.
三、概念剖析
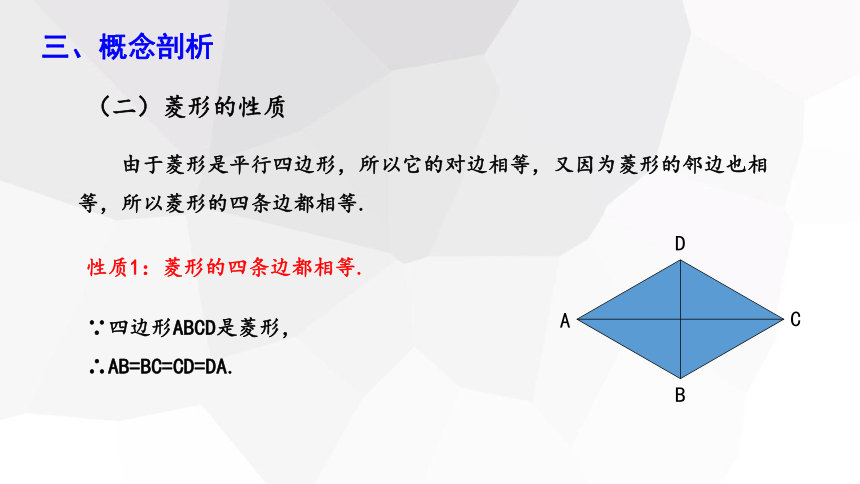
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
由于菱形是平行四边形,所以它的对边相等,又因为菱形的邻边也相等,所以菱形的四条边都相等.
三、概念剖析
(二)菱形的性质
A
B
C
D
性质1:菱形的四条边都相等.
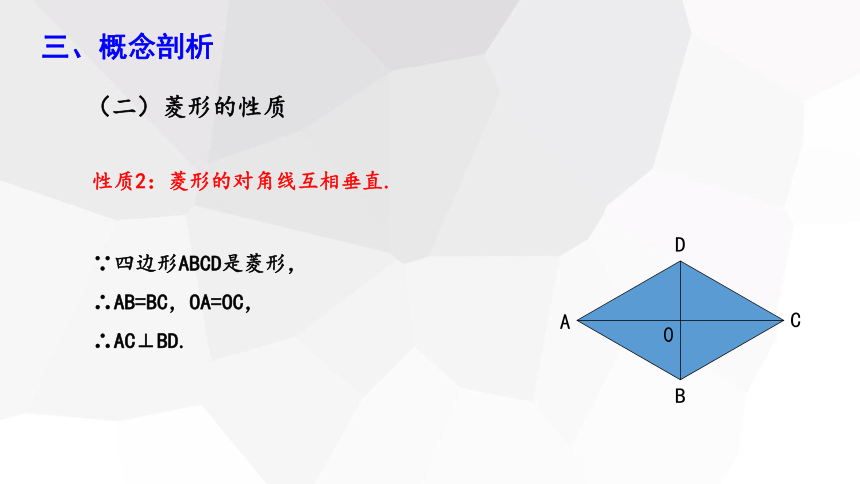
性质2:菱形的对角线互相垂直.
三、概念剖析
∵四边形ABCD是菱形,
∴AB=BC,OA=OC,
∴AC⊥BD.
A
B
C
D
0
(二)菱形的性质
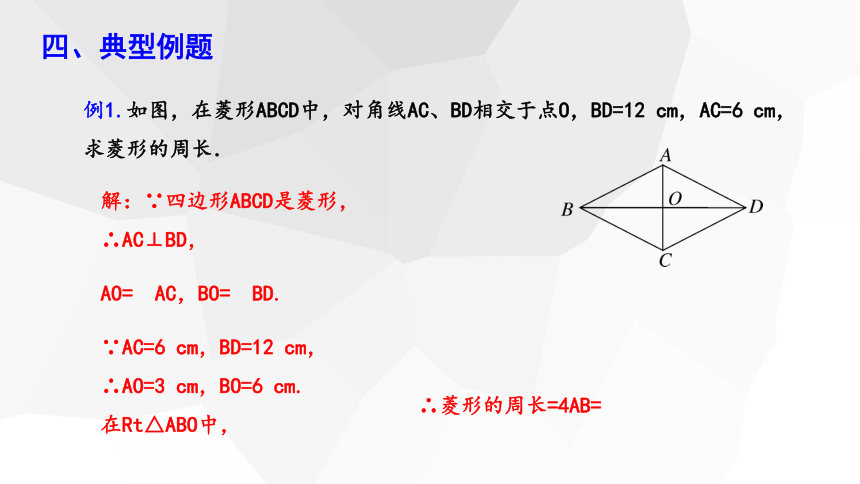
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12 cm,AC=6 cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
四、典型例题
AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,
∴菱形的周长=4AB=
小结:
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
性质1:菱形的四条边都相等.
性质2:菱形的对角线互相垂直.
四、典型例题
菱形的周长=边长的4倍.
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( )
A.10 B.12 C.15 D.20
C
分析:∵四边形ABCD是菱形,∴AB=AD.
又∵∠A=60°,∴△ABD是等边三角形.
∴△ABD的周长=3AB=15.
【当堂检测】
2.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
【当堂检测】
6 cm
分析:∵菱形ABCD的周长为48 cm,
∴AD=12,AC⊥BD,
∵E是AD的中点,
∴OE= AD=6(cm).
例2.如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H,求DH的长.
解:∵四边形ABCD是菱形,设AB,CD交于O点,
四、典型例题
在Rt△AOB中,
∵S菱形ABCD=
O
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,BD=6,
∴AO=4,BO=3,∠AOB=90°,
总结:
菱形的面积=底×高=对角线乘积的一半.
四、典型例题
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC+S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
分析:设BE=x,则EC=4-x,根据勾股定理求出x的值,由菱形的性质得到EC的长,即可求出菱形AECF的面积.
解:设BE=x,则EC=4-x,
∵四边形ABCD是矩形,
∴AE=EC=4-x,
在Rt△ABE中,AB +BE =AE ,即2 +x =(4-x) ,
【当堂检测】
3.如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,
求四边形AECF的面积.
解得x=1.5,
故EC=2.5,
S四边形AECF=EC×AB=2.5×2=5(cm) .
例3.如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
四、典型例题
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.(AAS)
∴AE=AF.
归纳:菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
4.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB, ∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA(ASA),
∴OA=EB.
【当堂检测】
A
B
C
D
O
E
菱形的性质
五、课堂总结
性质1:菱形的四条边都相等.
性质2:菱形的对角线互相垂直.
有关计算:
周长=边长的四倍,
面积=底×高=两条对角线乘积的一半.
第十九章 四边形
19.3 矩形、菱形、正方形
第1课时
1.了解菱形的概念及其与平行四边形的关系
2.探索并证明菱形的性质定理
3.应用菱形的性质定理解决相关计算或证明问题
一、学习目标
欣赏下面图片,图片中框出的图形是你熟悉的吗?
二、新课导入
(一)菱形的概念
定义:有一组邻边相等的平行四边形叫做菱形.
注意:①菱形是特殊的平行四边形.
②平行四边形不一定是菱形.
三、概念剖析
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
由于菱形是平行四边形,所以它的对边相等,又因为菱形的邻边也相等,所以菱形的四条边都相等.
三、概念剖析
(二)菱形的性质
A
B
C
D
性质1:菱形的四条边都相等.
性质2:菱形的对角线互相垂直.
三、概念剖析
∵四边形ABCD是菱形,
∴AB=BC,OA=OC,
∴AC⊥BD.
A
B
C
D
0
(二)菱形的性质
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12 cm,AC=6 cm,求菱形的周长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,
四、典型例题
AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,
∴菱形的周长=4AB=
小结:
菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
性质1:菱形的四条边都相等.
性质2:菱形的对角线互相垂直.
四、典型例题
菱形的周长=边长的4倍.
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( )
A.10 B.12 C.15 D.20
C
分析:∵四边形ABCD是菱形,∴AB=AD.
又∵∠A=60°,∴△ABD是等边三角形.
∴△ABD的周长=3AB=15.
【当堂检测】
2.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
【当堂检测】
6 cm
分析:∵菱形ABCD的周长为48 cm,
∴AD=12,AC⊥BD,
∵E是AD的中点,
∴OE= AD=6(cm).
例2.如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H,求DH的长.
解:∵四边形ABCD是菱形,设AB,CD交于O点,
四、典型例题
在Rt△AOB中,
∵S菱形ABCD=
O
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,BD=6,
∴AO=4,BO=3,∠AOB=90°,
总结:
菱形的面积=底×高=对角线乘积的一半.
四、典型例题
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC+S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
分析:设BE=x,则EC=4-x,根据勾股定理求出x的值,由菱形的性质得到EC的长,即可求出菱形AECF的面积.
解:设BE=x,则EC=4-x,
∵四边形ABCD是矩形,
∴AE=EC=4-x,
在Rt△ABE中,AB +BE =AE ,即2 +x =(4-x) ,
【当堂检测】
3.如图,四边形ABCD是矩形,四边形AECF是菱形,若AB=2 cm,BC=4 cm,
求四边形AECF的面积.
解得x=1.5,
故EC=2.5,
S四边形AECF=EC×AB=2.5×2=5(cm) .
例3.如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
四、典型例题
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.(AAS)
∴AE=AF.
归纳:菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
4.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB, ∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA(ASA),
∴OA=EB.
【当堂检测】
A
B
C
D
O
E
菱形的性质
五、课堂总结
性质1:菱形的四条边都相等.
性质2:菱形的对角线互相垂直.
有关计算:
周长=边长的四倍,
面积=底×高=两条对角线乘积的一半.
