19.3.2 菱形 第2课时 课件(共16张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.3.2 菱形 第2课时 课件(共16张PPT) 2023-2024学年初中数学沪科版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 154.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:58:14 | ||
图片预览



文档简介
(共16张PPT)
第十九章 四边形
19.3 矩形、菱形、正方形
第2课时
1.通过菱形的判定过程,掌握菱形的判定定理
2.会用这些菱形的判定方法进行有关的证明和计算
一、学习目标
复习引入
二、新课导入
菱形的定义是什么?性质有哪些?
一组邻边相等
有一组邻边相等的平行四边形叫做菱形.
平行四边形
菱形
1.四条边都相等
2.对角线互相垂直
菱形的性质
(一)用定义判定菱形
数学语言
思考:还有其他的判定方法吗?
三、概念剖析
A
B
C
D
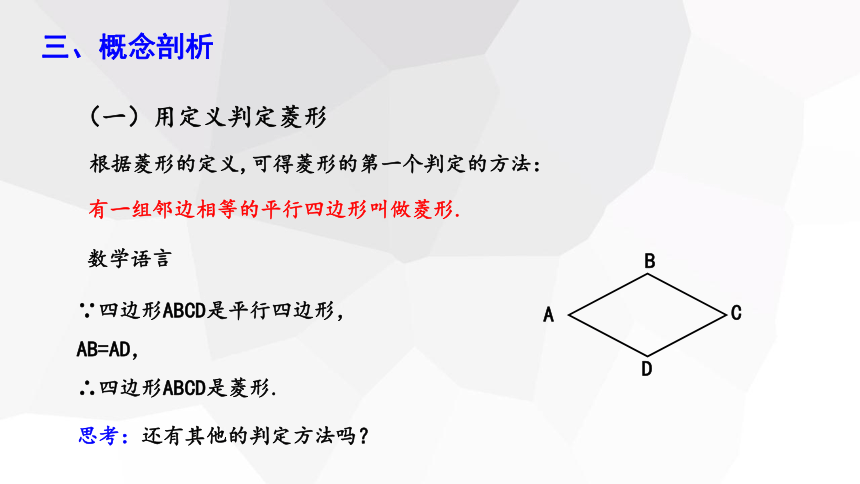
根据菱形的定义,可得菱形的第一个判定的方法:
有一组邻边相等的平行四边形叫做菱形.
∵四边形ABCD是平行四边形,
AB=AD,
∴四边形ABCD是菱形.
判定四边形为菱形的方法:
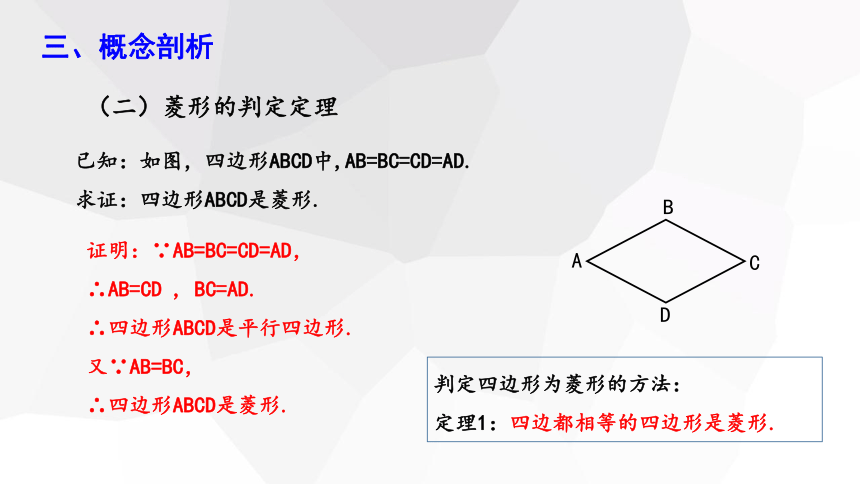
定理1:四边都相等的四边形是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
三、概念剖析
(二)菱形的判定定理
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
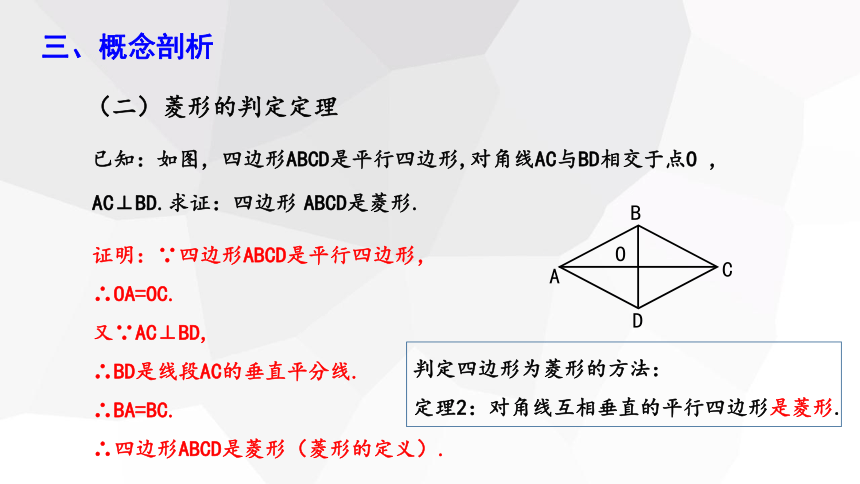
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.求证:四边形 ABCD是菱形.
三、概念剖析
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
(二)菱形的判定定理
A
B
C
O
D
判定四边形为菱形的方法:
定理2:对角线互相垂直的平行四边形是菱形.
例1.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
四、典型例题
A
B
C
D
O
点拨:首先由勾股定理的逆定理证明△AOB是直角三角形,从而得到AC⊥BD,然后根据对角线互相垂直的平行四边形是菱形判定即可.
总结:
菱形的判定定理:
定理1:四边都相等的四边形是菱形.
四、典型例题
定理2:对角线互相垂直的平行四边形是菱形.
1.判断下列说法是否正确:
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形.
√
【当堂检测】
分析:(1)对角线互相垂直的平行四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形.
×
2.一边长为5cm平行四边形的两条对角线的长分别为24cm和26cm,那么平行四边形的面积是 .
【当堂检测】
312 cm
分析:根据勾股定理的逆定理证明两条对角线垂直,然后根据对角线互相垂直的平行四边形判定菱形,根据菱形的面积=对角线乘积的一半计算即可.
例2.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,又∵F是DE延长线上的点,即EF∥BC,
∴四边形BCFE是平行四边形.
∵EF=BE,
∴四边形BCFE是菱形.
四、典型例题
点拨:首先根据中位线定理及线段关系证明四边形BCEF是平行四边形,然后根据有一组邻边相等的平行四边形是菱形判定即可.
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BC=CE=4,
四、典型例题
∴BC边上的高为
∴菱形BCEF的面积为
点拨:首先根据已知条件得到△EBC是等边三角形,然后由勾股定理求得菱形的高,根据菱形的面积公式求解.
小结:
判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
四、典型例题
菱形的面积=底×高=对角线乘积的一半.
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
B
【当堂检测】
分析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ABED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
分析:求平行四边形ABCD的周长可先证明平行四边形ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,AB=BC,
∴平行四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
【当堂检测】
4.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.
五、课堂总结
菱形的判定:
定理1:四边都相等的四边形是菱形.
定理2:对角线互相垂直的平行四边形是菱形.
第十九章 四边形
19.3 矩形、菱形、正方形
第2课时
1.通过菱形的判定过程,掌握菱形的判定定理
2.会用这些菱形的判定方法进行有关的证明和计算
一、学习目标
复习引入
二、新课导入
菱形的定义是什么?性质有哪些?
一组邻边相等
有一组邻边相等的平行四边形叫做菱形.
平行四边形
菱形
1.四条边都相等
2.对角线互相垂直
菱形的性质
(一)用定义判定菱形
数学语言
思考:还有其他的判定方法吗?
三、概念剖析
A
B
C
D
根据菱形的定义,可得菱形的第一个判定的方法:
有一组邻边相等的平行四边形叫做菱形.
∵四边形ABCD是平行四边形,
AB=AD,
∴四边形ABCD是菱形.
判定四边形为菱形的方法:
定理1:四边都相等的四边形是菱形.
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
三、概念剖析
(二)菱形的判定定理
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.求证:四边形 ABCD是菱形.
三、概念剖析
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
(二)菱形的判定定理
A
B
C
O
D
判定四边形为菱形的方法:
定理2:对角线互相垂直的平行四边形是菱形.
例1.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
四、典型例题
A
B
C
D
O
点拨:首先由勾股定理的逆定理证明△AOB是直角三角形,从而得到AC⊥BD,然后根据对角线互相垂直的平行四边形是菱形判定即可.
总结:
菱形的判定定理:
定理1:四边都相等的四边形是菱形.
四、典型例题
定理2:对角线互相垂直的平行四边形是菱形.
1.判断下列说法是否正确:
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形.
√
【当堂检测】
分析:(1)对角线互相垂直的平行四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形.
×
2.一边长为5cm平行四边形的两条对角线的长分别为24cm和26cm,那么平行四边形的面积是 .
【当堂检测】
312 cm
分析:根据勾股定理的逆定理证明两条对角线垂直,然后根据对角线互相垂直的平行四边形判定菱形,根据菱形的面积=对角线乘积的一半计算即可.
例2.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,又∵F是DE延长线上的点,即EF∥BC,
∴四边形BCFE是平行四边形.
∵EF=BE,
∴四边形BCFE是菱形.
四、典型例题
点拨:首先根据中位线定理及线段关系证明四边形BCEF是平行四边形,然后根据有一组邻边相等的平行四边形是菱形判定即可.
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BC=CE=4,
四、典型例题
∴BC边上的高为
∴菱形BCEF的面积为
点拨:首先根据已知条件得到△EBC是等边三角形,然后由勾股定理求得菱形的高,根据菱形的面积公式求解.
小结:
判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
四、典型例题
菱形的面积=底×高=对角线乘积的一半.
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
B
【当堂检测】
分析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ABED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
分析:求平行四边形ABCD的周长可先证明平行四边形ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,AB=BC,
∴平行四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.
【当堂检测】
4.如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.
五、课堂总结
菱形的判定:
定理1:四边都相等的四边形是菱形.
定理2:对角线互相垂直的平行四边形是菱形.
