19.3.3 正方形 第1课时 课件(共20张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.3.3 正方形 第1课时 课件(共20张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 857.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
第十九章 四边形
19.3.3 矩形、菱形、正方形
第1课时
1.探索并证明正方形的性质,并了解正方形与平行四边形、矩形、菱形之间的联系和区别
2.会运用正方形的性质进行有关的论证和计算
一、学习目标
情景引入
二、新课导入
你还能举出其他的例子吗?
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
(一)正方形的定义
三、概念剖析
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
⑴有一个角是直角的平行四边形(矩形)
⑵并且有一组邻边相等的平行四边形(菱形)
两层含义
正方形
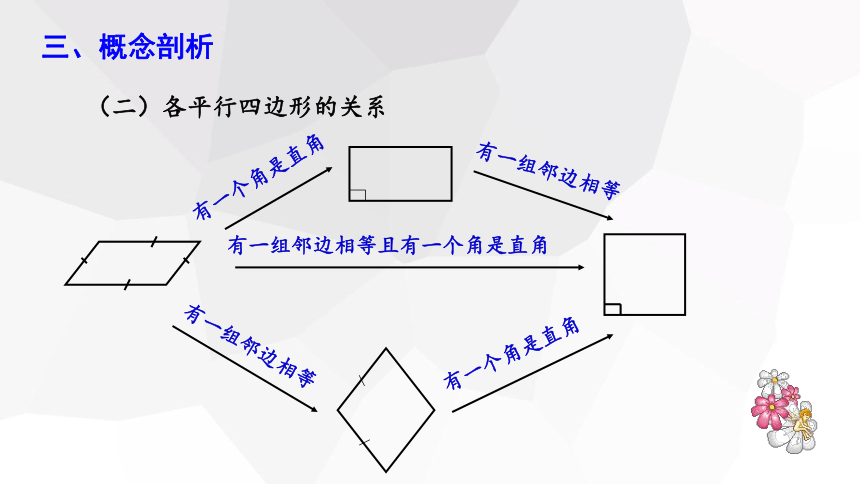
三、概念剖析
(二)各平行四边形的关系
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
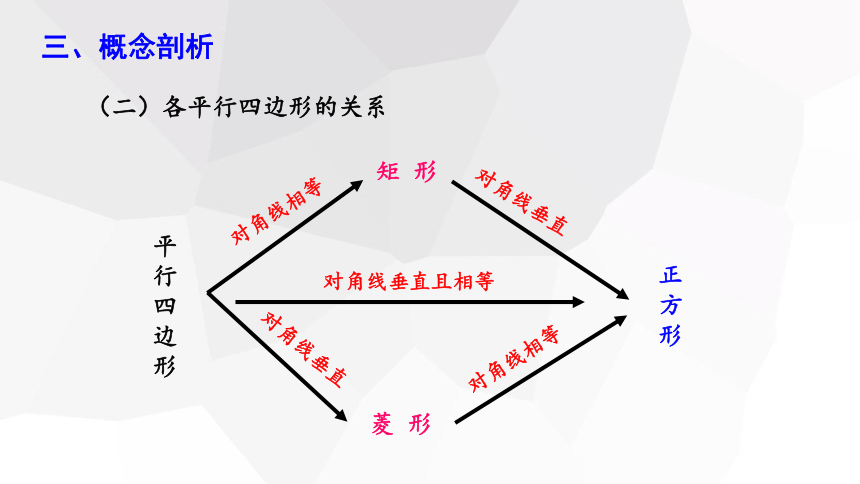
三、概念剖析
(二)各平行四边形的关系
平行四边形
矩 形
菱 形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
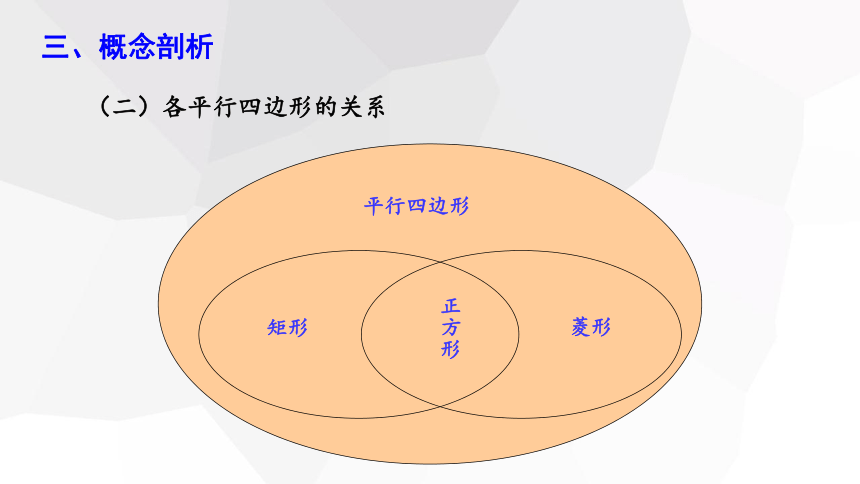
三、概念剖析
(二)各平行四边形的关系
平行四边形
矩形
菱形
正方形
三、概念剖析
(三)正方形的性质
正方形不仅是平行四边形、矩形,还是菱形.正方形具有平行四边形、矩形、菱形的一切性质.
性质1:四条边都相等,四个角都是直角.
性质2:正方形的对角线相等且互相垂直平分.
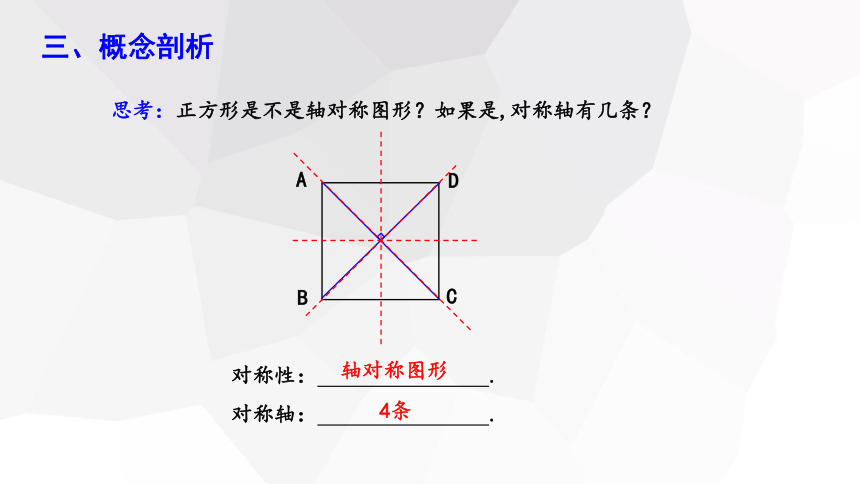
三、概念剖析
思考:正方形是不是轴对称图形?如果是,对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
例1.如图,在正方形ABCD中,ΔBEC是等边三角形,
求证:∠EAD=∠EDA=15°.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
四、典型例题
点拨:由正方形ABCD和△BEC是等边三角形可得△ABE和△DCE是等腰三角形,得到∠BAE和∠CDE的度数,从而证明即可.
总结:
正方形的性质:
性质1:四条边都相等,四个角都是直角.
四、典型例题
1.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数
是 .
【当堂检测】
分析:解:在正方形ABCD中,∠BAD=90°,AB=AE,
又∵△ADE是正三角形,
∴∠DAE=∠AED=60°,
∴∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴∠ABE=∠AEB=15°,∠BED=∠AED-∠AEB=60°-15°=45°.
45°
2.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
【当堂检测】
点拨:由PB=PC得∠PBC=∠PCB,从而得到∠ABP=∠DCP,又AB=DC,PB=PC,可证△APB≌△DPC.
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC(SAS).
(2)求证:∠BAP=2∠PAC.
点拨:由(1)得∠BAC=∠DAC=45°,△PAD是等边三角形,可求得PAC=∠DAP-∠DAC=15°,∠BAP=∠BAC-∠PAC=30°,据此证明结论.
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°,
∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
【当堂检测】
例2.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
点拨:连接PC,根据正方形的性质可证明△ADP≌CDP(SAS),由此得PA=PC,又四边形PECF是矩形,PC=EF,可得结论.
四、典型例题
A
B
C
D
P
E
F
解:连接PC,
∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45°,
∴△ADP≌CDP(SAS),
∴AP=PC.
又∵PE⊥BC,PF⊥DC,
∴四边形PECF是矩形,∴PC=EF.
∴AP=EF.
想一想:你还有其他的解题方法吗?
四、典型例题
A
B
C
D
P
E
F
方法二:
解:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC,PF⊥DC,
∴四边形PECF是矩形,∴PC=EF.
∴AP=EF.
总结:
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
四、典型例题
性质2:对角线相等且互相垂直平分.
3.正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
【当堂检测】
分析:正方形的性质:正方形的四条边相等,四个角都是直角,对角线互相垂直平分且相等,并且每一条对角线平分一组对角;菱形的性质:菱形的四条边相等,对角线互相垂直平分,并且每一条对角线平分一组对角.
因此,正方形具有而菱形不一定具有的性质是对角线相等.
D
分析:根据正方形的性质可得AC⊥BD,AO=OD=2,由勾股定理得正方形的边长,据此可求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
在Rt△AOD中,由勾股定理,得
【当堂检测】
4.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∴正方形的周长为4AD= ,面积为AD2=8.
五、课堂总结
正方形的性质:
性质1:四条边都相等,四个角都是直角.
性质2:正方形的对角线相等且互相垂直平分.
第十九章 四边形
19.3.3 矩形、菱形、正方形
第1课时
1.探索并证明正方形的性质,并了解正方形与平行四边形、矩形、菱形之间的联系和区别
2.会运用正方形的性质进行有关的论证和计算
一、学习目标
情景引入
二、新课导入
你还能举出其他的例子吗?
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
(一)正方形的定义
三、概念剖析
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
⑴有一个角是直角的平行四边形(矩形)
⑵并且有一组邻边相等的平行四边形(菱形)
两层含义
正方形
三、概念剖析
(二)各平行四边形的关系
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
三、概念剖析
(二)各平行四边形的关系
平行四边形
矩 形
菱 形
正方形
对角线相等
对角线垂直
对角线相等
对角线垂直
对角线垂直且相等
三、概念剖析
(二)各平行四边形的关系
平行四边形
矩形
菱形
正方形
三、概念剖析
(三)正方形的性质
正方形不仅是平行四边形、矩形,还是菱形.正方形具有平行四边形、矩形、菱形的一切性质.
性质1:四条边都相等,四个角都是直角.
性质2:正方形的对角线相等且互相垂直平分.
三、概念剖析
思考:正方形是不是轴对称图形?如果是,对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
例1.如图,在正方形ABCD中,ΔBEC是等边三角形,
求证:∠EAD=∠EDA=15°.
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
四、典型例题
点拨:由正方形ABCD和△BEC是等边三角形可得△ABE和△DCE是等腰三角形,得到∠BAE和∠CDE的度数,从而证明即可.
总结:
正方形的性质:
性质1:四条边都相等,四个角都是直角.
四、典型例题
1.如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数
是 .
【当堂检测】
分析:解:在正方形ABCD中,∠BAD=90°,AB=AE,
又∵△ADE是正三角形,
∴∠DAE=∠AED=60°,
∴∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴∠ABE=∠AEB=15°,∠BED=∠AED-∠AEB=60°-15°=45°.
45°
2.如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
【当堂检测】
点拨:由PB=PC得∠PBC=∠PCB,从而得到∠ABP=∠DCP,又AB=DC,PB=PC,可证△APB≌△DPC.
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC(SAS).
(2)求证:∠BAP=2∠PAC.
点拨:由(1)得∠BAC=∠DAC=45°,△PAD是等边三角形,可求得PAC=∠DAP-∠DAC=15°,∠BAP=∠BAC-∠PAC=30°,据此证明结论.
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°,
∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
【当堂检测】
例2.如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
点拨:连接PC,根据正方形的性质可证明△ADP≌CDP(SAS),由此得PA=PC,又四边形PECF是矩形,PC=EF,可得结论.
四、典型例题
A
B
C
D
P
E
F
解:连接PC,
∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45°,
∴△ADP≌CDP(SAS),
∴AP=PC.
又∵PE⊥BC,PF⊥DC,
∴四边形PECF是矩形,∴PC=EF.
∴AP=EF.
想一想:你还有其他的解题方法吗?
四、典型例题
A
B
C
D
P
E
F
方法二:
解:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC,PF⊥DC,
∴四边形PECF是矩形,∴PC=EF.
∴AP=EF.
总结:
在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
四、典型例题
性质2:对角线相等且互相垂直平分.
3.正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
【当堂检测】
分析:正方形的性质:正方形的四条边相等,四个角都是直角,对角线互相垂直平分且相等,并且每一条对角线平分一组对角;菱形的性质:菱形的四条边相等,对角线互相垂直平分,并且每一条对角线平分一组对角.
因此,正方形具有而菱形不一定具有的性质是对角线相等.
D
分析:根据正方形的性质可得AC⊥BD,AO=OD=2,由勾股定理得正方形的边长,据此可求正方形的周长与面积.
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
在Rt△AOD中,由勾股定理,得
【当堂检测】
4.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∴正方形的周长为4AD= ,面积为AD2=8.
五、课堂总结
正方形的性质:
性质1:四条边都相等,四个角都是直角.
性质2:正方形的对角线相等且互相垂直平分.
