2023-2024学年初中数学沪科版八年级下册19.3.3 正方形 第2课时课件(共15张PPT)
文档属性
| 名称 | 2023-2024学年初中数学沪科版八年级下册19.3.3 正方形 第2课时课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 207.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:04:52 | ||
图片预览





文档简介
(共15张PPT)
第十九章 四边形
19.3.3 矩形、菱形、正方形
第2课时
1.探索并证明正方形的判定,并了解平行四边形、矩形、菱形之间的联系和区别
2.会运用正方形的判定条件进行有关的论证
一、学习目标
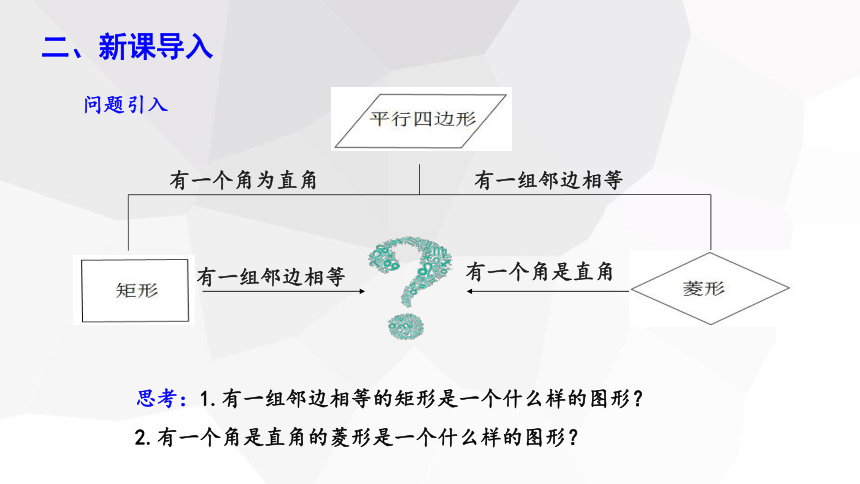
问题引入
二、新课导入
思考:1.有一组邻边相等的矩形是一个什么样的图形?
2.有一个角是直角的菱形是一个什么样的图形?
有一个角为直角
有一组邻边相等
有一组邻边相等
有一个角是直角
(一)正方形的判定
三、概念剖析
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
①有一个角是直角的平行四边形(矩形);
②有一组邻边相等的平行四边形(菱形).
三、概念剖析
(一)正方形的判定
1.四条边相等,四个角都是直角的四边形叫做正方形.
2.正方形既是菱形,又是矩形.即
(1)有一组邻边相等的矩形是正方形.
(2)有一个角是直角的菱形是正方形.
三、概念剖析
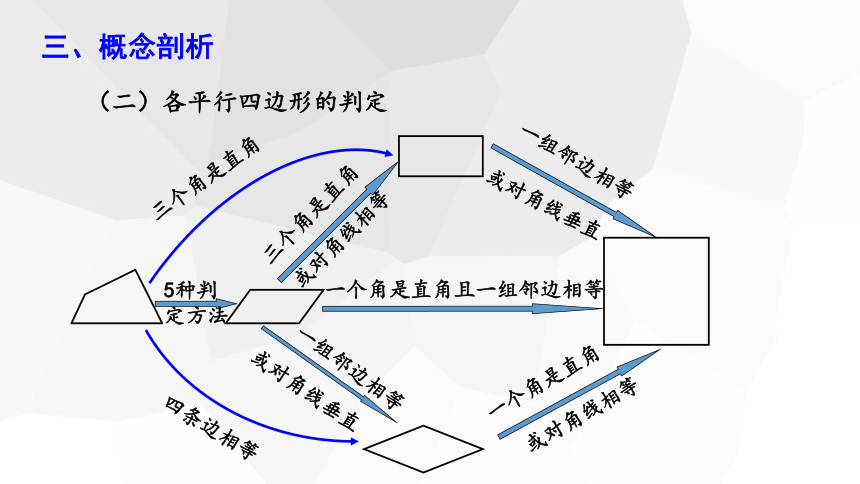
(二)各平行四边形的判定
5种判定方法
三个角是直角
四条边相等
三个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
例1.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
点拨:由题意得,四边形CFDE是矩形,根据角平分线的性质可得DE=DF,据此判定四边形CFDE是正方形.
四、典型例题
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.
总结:
正方形的判定
1.正方形的定义:有一个角是直角,且有一组邻边相等的平行四边形是正方形.
四、典型例题
2.有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形.
3.正方形既是矩形,也是菱形,同时也是特殊的平行四边形.
1.已知在四边形ABCD中,∠A=∠B=∠C=90°,下列可以判定四边形是正方形的是( )
A.∠D=90° B.AB=CD C.AC=BD D.BC=CD
【当堂检测】
分析:四边形ABCD中,∠A=∠B=∠C=90°,能使这个四边形是正方形的是邻边相等,即BC=CD.
D
2.平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: 使得平行四边形ABCD是正方形.
【当堂检测】
分析:∵平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴平行四边形ABCD是菱形,
当∠BAD=90°时,平行四边形ABCD是正方形(有一个角是直角的菱形是正方形);
当AC=BD时,平行四边形ABCD是正方形(对角线相等的菱形是正方形).
∠BAD=90°或AC=BD
例2.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
点拨:根据正方形的性质判定△ABF≌△ADE后即可证明.
四、典型例题
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠DAE,
又∵AF=AE,
∴△ABF≌△ADE(SAS),
∴BF=DE.
(2)当点E运动到AC中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?说明理由.
四、典型例题
分析:利用正方形的判定方法判定即可.
解:当点E运动到AC的中点时四边形AFBE是正方形.
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEA=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE为平行四边形,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
分析:由垂直的定义得出∠DEC=∠DFC=90°,由角平分线和平角的定义得∠ECF=90°,即可证明四边形DECF是矩形.
证明:(1)∵DE⊥CE,DF⊥CF,
∴∠DEC=∠DFC=90°,
∵CE平分∠BCD,CF平分∠GCD,
【当堂检测】
3.如图,在四边形ABCD中,点G在BC的延长线上,CE平分∠BCD,CF平分∠GCD,过点D作DE⊥CE于点E,DF⊥CF于点F.
(1)求证:四边形DECF是矩形;
∴∠DCE= ∠BCD,∠DCF= ∠DCG,
∴∠DCE+∠DCF= (∠BCD+∠DCG)=90°,
即∠ECF=90°,
∴四边形DECF是矩形.
分析:由正方形的判定即可得出结论.
解:添加条件:DE=CE.
【当堂检测】
(2)添加一个条件 ,使四边形DECF是正方形(不用证明).
DE=CE(答案不唯一)
点拨:有一组邻边相等的矩形是正方形.
五、课堂总结
正方形的判定:
有一个角是直角,且有一组邻边相等的平行四边形是正方形.
有一组邻边相等的矩形是正方形;
对角线互相垂直的矩形是正方形.
有一个角是直角的菱形是正方形;
对角线相等的菱形是正方形.
第十九章 四边形
19.3.3 矩形、菱形、正方形
第2课时
1.探索并证明正方形的判定,并了解平行四边形、矩形、菱形之间的联系和区别
2.会运用正方形的判定条件进行有关的论证
一、学习目标
问题引入
二、新课导入
思考:1.有一组邻边相等的矩形是一个什么样的图形?
2.有一个角是直角的菱形是一个什么样的图形?
有一个角为直角
有一组邻边相等
有一组邻边相等
有一个角是直角
(一)正方形的判定
三、概念剖析
有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
①有一个角是直角的平行四边形(矩形);
②有一组邻边相等的平行四边形(菱形).
三、概念剖析
(一)正方形的判定
1.四条边相等,四个角都是直角的四边形叫做正方形.
2.正方形既是菱形,又是矩形.即
(1)有一组邻边相等的矩形是正方形.
(2)有一个角是直角的菱形是正方形.
三、概念剖析
(二)各平行四边形的判定
5种判定方法
三个角是直角
四条边相等
三个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
例1.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
点拨:由题意得,四边形CFDE是矩形,根据角平分线的性质可得DE=DF,据此判定四边形CFDE是正方形.
四、典型例题
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.
总结:
正方形的判定
1.正方形的定义:有一个角是直角,且有一组邻边相等的平行四边形是正方形.
四、典型例题
2.有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形.
3.正方形既是矩形,也是菱形,同时也是特殊的平行四边形.
1.已知在四边形ABCD中,∠A=∠B=∠C=90°,下列可以判定四边形是正方形的是( )
A.∠D=90° B.AB=CD C.AC=BD D.BC=CD
【当堂检测】
分析:四边形ABCD中,∠A=∠B=∠C=90°,能使这个四边形是正方形的是邻边相等,即BC=CD.
D
2.平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件: 使得平行四边形ABCD是正方形.
【当堂检测】
分析:∵平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,
∴平行四边形ABCD是菱形,
当∠BAD=90°时,平行四边形ABCD是正方形(有一个角是直角的菱形是正方形);
当AC=BD时,平行四边形ABCD是正方形(对角线相等的菱形是正方形).
∠BAD=90°或AC=BD
例2.如图,正方形ABCD,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE;
点拨:根据正方形的性质判定△ABF≌△ADE后即可证明.
四、典型例题
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AF⊥AC,∴∠EAF=90°,
∴∠BAF=∠DAE,
又∵AF=AE,
∴△ABF≌△ADE(SAS),
∴BF=DE.
(2)当点E运动到AC中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?说明理由.
四、典型例题
分析:利用正方形的判定方法判定即可.
解:当点E运动到AC的中点时四边形AFBE是正方形.
理由:∵点E运动到AC的中点,AB=BC,
∴BE⊥AC,BE=AE= AC,
∵AF=AE,
∴BE=AF=AE.
又∵BE⊥AC,∠FAE=∠BEA=90°,
∴BE∥AF,
∵BE=AF,
∴四边形AFBE为平行四边形,
∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
分析:由垂直的定义得出∠DEC=∠DFC=90°,由角平分线和平角的定义得∠ECF=90°,即可证明四边形DECF是矩形.
证明:(1)∵DE⊥CE,DF⊥CF,
∴∠DEC=∠DFC=90°,
∵CE平分∠BCD,CF平分∠GCD,
【当堂检测】
3.如图,在四边形ABCD中,点G在BC的延长线上,CE平分∠BCD,CF平分∠GCD,过点D作DE⊥CE于点E,DF⊥CF于点F.
(1)求证:四边形DECF是矩形;
∴∠DCE= ∠BCD,∠DCF= ∠DCG,
∴∠DCE+∠DCF= (∠BCD+∠DCG)=90°,
即∠ECF=90°,
∴四边形DECF是矩形.
分析:由正方形的判定即可得出结论.
解:添加条件:DE=CE.
【当堂检测】
(2)添加一个条件 ,使四边形DECF是正方形(不用证明).
DE=CE(答案不唯一)
点拨:有一组邻边相等的矩形是正方形.
五、课堂总结
正方形的判定:
有一个角是直角,且有一组邻边相等的平行四边形是正方形.
有一组邻边相等的矩形是正方形;
对角线互相垂直的矩形是正方形.
有一个角是直角的菱形是正方形;
对角线相等的菱形是正方形.
