19.4 综合与实践 多边形的镶嵌 课件(共18张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 19.4 综合与实践 多边形的镶嵌 课件(共18张PPT) 2023-2024学年初中数学沪科版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:00:56 | ||
图片预览





文档简介
(共18张PPT)
第十九章 四边形
19.4 综合与实践 多边形的镶嵌
1.知道平面镶嵌的意义,会用一种或多种正多边形进行平面镶嵌
2.知道可以用一些全等的非正多边形进行平面镶嵌
一、学习目标
二、新课导入
思考:在生活中有没有遇到正五边形的瓷砖铺成的地面或墙面?为什么?
情景引入
(一)平面镶嵌的定义
三、概念剖析
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
三、概念剖析
(二)镶嵌的条件
正三角形、正方形、正六边形都可以用来作平面镶嵌,正五边形却不能用来作平面镶嵌.
用一种正多边形作平面镶嵌是比较简单的图形.
思考:你知道原因吗?
三、概念剖析
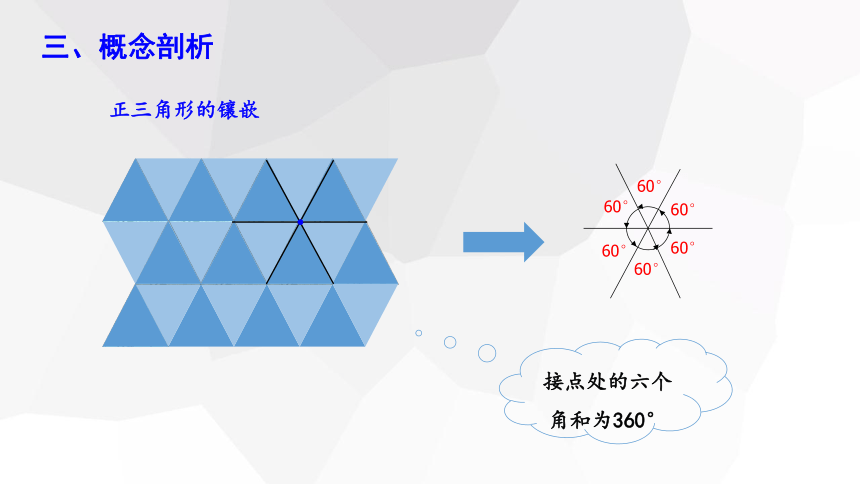
60°
60°
60°
60°
60°
60°
接点处的六个
角和为360°
正三角形的镶嵌
三、概念剖析
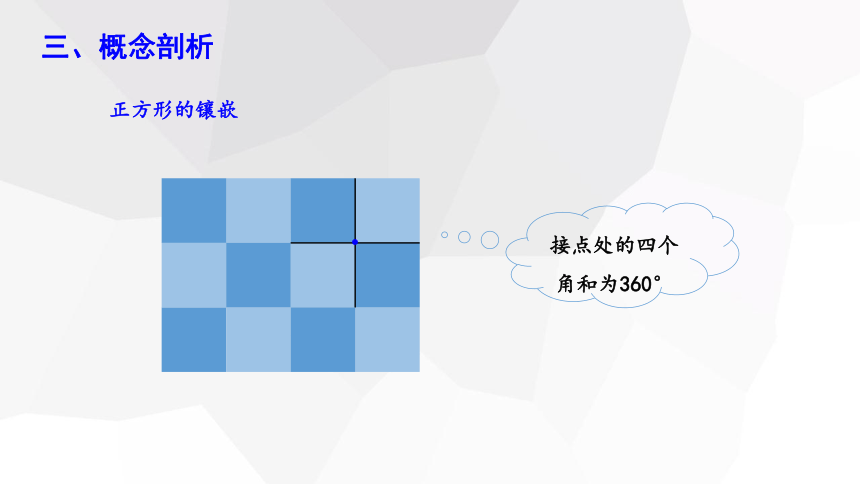
正方形的镶嵌
接点处的四个
角和为360°
三、概念剖析
正五边形的镶嵌
接点处的3个角和不等于360°
三、概念剖析
归纳:同一种正多边形能够平面镶嵌的条件:360°是它内角的整数倍.
正六边形的镶嵌
接点处的3个角和等于360°
三、概念剖析
我们发现能够镶嵌成平面图案的组合有:正三角形和正方形,正三角形和正六边形.
用两种正多边形镶嵌平面
归纳:几种正多边形能够平面镶嵌的条件:它们内角的倍数相加等于360°.
三、概念剖析
形状、大小完全相同的任意三角形 、四边形都可以镶嵌平面.
用一种非正多边形镶嵌平面
归纳:多边形能够平面镶嵌的条件:拼接在同一个顶点的各个角的和恰好等于360°且相邻的多边形有公共边.
例1.现有六种地板砖,它们的形状分别是:正三角形、正方形、正五边形、正六边形、正八边形、正十边形,且它们的边长都相等.若同时选择其中两种地板砖铺地面(不能有缝隙),选择的方式有哪几种?
点拨:能够平面镶嵌的条件是它们内角的倍数相加等于360°.
四、典型例题
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是60°、90°、108°、120°、135°、150°.
正三角形 + 正方形:60°×3 + 90°×2 = 360°,
正三角形 + 正六边形:60°×4 + 120°×1 = 360°,
正方形 + 正八边形:90°×1 + 135°×2 = 360°,
正三角形 + 正十二边形:60°×1 + 150°×2 = 360°.
四、典型例题
答:选择的方式有4种,分别是:正三角形 + 正方形,正三角形 + 正
六边形,正方形 + 正八边形,正三角形 + 正十二边形.
总结:
多边形的镶嵌
平面镶嵌的原则:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
四、典型例题
平面镶嵌的常用方法:
(1)只用一种正多边形;(2)同时用两种正多边形;(3)用非正多边形.
1.下列图形中,单独选用一种图形不能进行平面镶嵌的是( )
A.正三角形 B.正六边形 C.正方形 D.正五边形
【当堂检测】
分析:几何图形镶嵌成平面的关键是围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角,360°为正多边形一个内角的整数倍才能单独镶嵌.
D
正五边形一个内角的度数是 =108°,不是360的约数,不能进行平面镶嵌.
2.在下列三组地板砖中,①正三角形与正方形,②正三角形与正六边形,③正方形与正六边形,将每组中的两种多边形结合,能镶嵌地面的
是 .
【当堂检测】
分析:正三角形、正方形、正六边形的内角分别为:60°,90°,120°.
① 3×60°+2×90°=360°,能镶嵌地面;
② 2×60°+2×120°=360°,或60°×4+120°=360°,能镶嵌地面;
③当m×90°+n×120°=360°时, ,显然n取任何正整数时,m不能得正整数,故不能镶嵌地面;
∴将每组中的两种多边形结合,能镶嵌地面的是①②.
①②
分析:利用两种正多边形镶嵌内角之间关系求解即可.
解:正五边形和正八边形镶嵌成平面图形如图.
设在一个顶点周围有m个正方形的角,n个正八边形的角,
那么m,n应是方程m×90°+n×135°=360°的正整数解,
即2m+3n=8的正整数解,只有m=1,n=2一组,
∴符合条件的图形只有一种.
【当堂检测】
3.王老师正准备装修新买房屋的地面,到一家装修公司去看地砖,结果王老师看中边长相等的正方形和正八边形的两种地砖的质量,你能帮助王老师用这两种正多边形镶嵌成一个平面图形(草图)吗?并探索这两种正多边形共能镶嵌成几种不同的平面图形,说明你的理由.
五、课堂总结
平面镶嵌
定义:用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
镶嵌的条件:(1)边长要相等;(2)有公共顶点;(3)在公共顶点处各内角的和为360°.
镶嵌的方法:(1)只用一种正多边形;(2)同时用两种正多边形;(3)用非正多边形.
第十九章 四边形
19.4 综合与实践 多边形的镶嵌
1.知道平面镶嵌的意义,会用一种或多种正多边形进行平面镶嵌
2.知道可以用一些全等的非正多边形进行平面镶嵌
一、学习目标
二、新课导入
思考:在生活中有没有遇到正五边形的瓷砖铺成的地面或墙面?为什么?
情景引入
(一)平面镶嵌的定义
三、概念剖析
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
三、概念剖析
(二)镶嵌的条件
正三角形、正方形、正六边形都可以用来作平面镶嵌,正五边形却不能用来作平面镶嵌.
用一种正多边形作平面镶嵌是比较简单的图形.
思考:你知道原因吗?
三、概念剖析
60°
60°
60°
60°
60°
60°
接点处的六个
角和为360°
正三角形的镶嵌
三、概念剖析
正方形的镶嵌
接点处的四个
角和为360°
三、概念剖析
正五边形的镶嵌
接点处的3个角和不等于360°
三、概念剖析
归纳:同一种正多边形能够平面镶嵌的条件:360°是它内角的整数倍.
正六边形的镶嵌
接点处的3个角和等于360°
三、概念剖析
我们发现能够镶嵌成平面图案的组合有:正三角形和正方形,正三角形和正六边形.
用两种正多边形镶嵌平面
归纳:几种正多边形能够平面镶嵌的条件:它们内角的倍数相加等于360°.
三、概念剖析
形状、大小完全相同的任意三角形 、四边形都可以镶嵌平面.
用一种非正多边形镶嵌平面
归纳:多边形能够平面镶嵌的条件:拼接在同一个顶点的各个角的和恰好等于360°且相邻的多边形有公共边.
例1.现有六种地板砖,它们的形状分别是:正三角形、正方形、正五边形、正六边形、正八边形、正十边形,且它们的边长都相等.若同时选择其中两种地板砖铺地面(不能有缝隙),选择的方式有哪几种?
点拨:能够平面镶嵌的条件是它们内角的倍数相加等于360°.
四、典型例题
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是60°、90°、108°、120°、135°、150°.
正三角形 + 正方形:60°×3 + 90°×2 = 360°,
正三角形 + 正六边形:60°×4 + 120°×1 = 360°,
正方形 + 正八边形:90°×1 + 135°×2 = 360°,
正三角形 + 正十二边形:60°×1 + 150°×2 = 360°.
四、典型例题
答:选择的方式有4种,分别是:正三角形 + 正方形,正三角形 + 正
六边形,正方形 + 正八边形,正三角形 + 正十二边形.
总结:
多边形的镶嵌
平面镶嵌的原则:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
四、典型例题
平面镶嵌的常用方法:
(1)只用一种正多边形;(2)同时用两种正多边形;(3)用非正多边形.
1.下列图形中,单独选用一种图形不能进行平面镶嵌的是( )
A.正三角形 B.正六边形 C.正方形 D.正五边形
【当堂检测】
分析:几何图形镶嵌成平面的关键是围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角,360°为正多边形一个内角的整数倍才能单独镶嵌.
D
正五边形一个内角的度数是 =108°,不是360的约数,不能进行平面镶嵌.
2.在下列三组地板砖中,①正三角形与正方形,②正三角形与正六边形,③正方形与正六边形,将每组中的两种多边形结合,能镶嵌地面的
是 .
【当堂检测】
分析:正三角形、正方形、正六边形的内角分别为:60°,90°,120°.
① 3×60°+2×90°=360°,能镶嵌地面;
② 2×60°+2×120°=360°,或60°×4+120°=360°,能镶嵌地面;
③当m×90°+n×120°=360°时, ,显然n取任何正整数时,m不能得正整数,故不能镶嵌地面;
∴将每组中的两种多边形结合,能镶嵌地面的是①②.
①②
分析:利用两种正多边形镶嵌内角之间关系求解即可.
解:正五边形和正八边形镶嵌成平面图形如图.
设在一个顶点周围有m个正方形的角,n个正八边形的角,
那么m,n应是方程m×90°+n×135°=360°的正整数解,
即2m+3n=8的正整数解,只有m=1,n=2一组,
∴符合条件的图形只有一种.
【当堂检测】
3.王老师正准备装修新买房屋的地面,到一家装修公司去看地砖,结果王老师看中边长相等的正方形和正八边形的两种地砖的质量,你能帮助王老师用这两种正多边形镶嵌成一个平面图形(草图)吗?并探索这两种正多边形共能镶嵌成几种不同的平面图形,说明你的理由.
五、课堂总结
平面镶嵌
定义:用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
镶嵌的条件:(1)边长要相等;(2)有公共顶点;(3)在公共顶点处各内角的和为360°.
镶嵌的方法:(1)只用一种正多边形;(2)同时用两种正多边形;(3)用非正多边形.
