20.2.1 数据的集中趋势 第1课时 课件 (共14张PPT)2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 20.2.1 数据的集中趋势 第1课时 课件 (共14张PPT)2023-2024学年初中数学沪科版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 179.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:01:20 | ||
图片预览





文档简介
(共14张PPT)
第二十章 数据的初步分析
20.2.1 数据的集中趋势
第1课时
1.掌握平均数的概念,会求一组数据的平均数
2.会用平均数解决实际生活中的问题
一、学习目标
二、新课导入
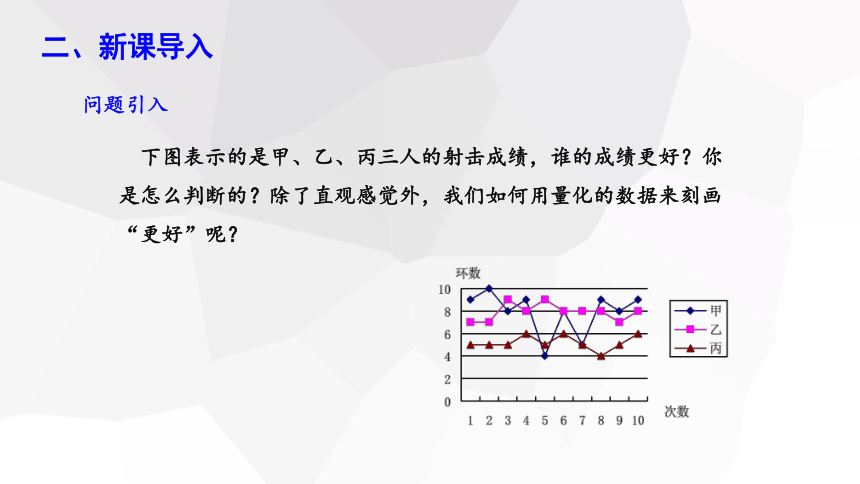
问题引入
下图表示的是甲、乙、丙三人的射击成绩,谁的成绩更好?你是怎么判断的?除了直观感觉外,我们如何用量化的数据来刻画“更好”呢?
平均数
三、概念剖析
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
例1.植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人).
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
典型例题
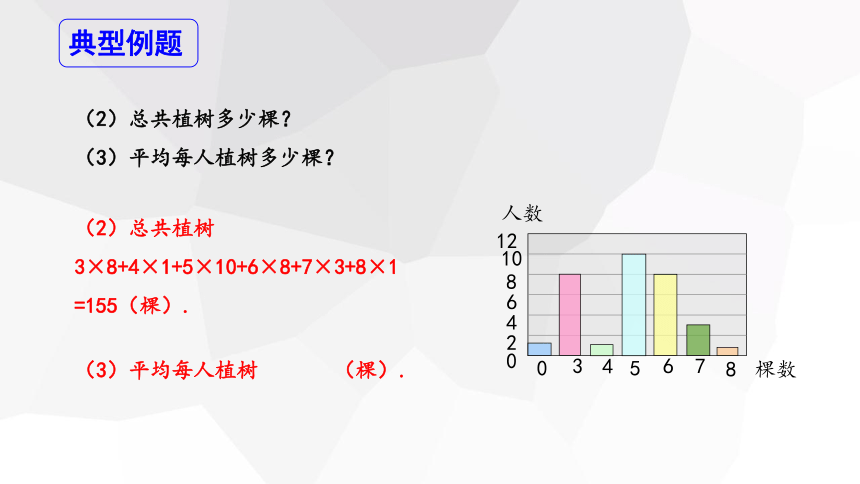
(2)总共植树多少棵?
(3)平均每人植树多少棵?
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1
=155(棵).
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
(3)平均每人植树 (棵).
典型例题
总结:
平均数
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
典型例题
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B.86 C.88 D.90
【当堂检测】
分析:由题意得,5名学生的总分是5×82=410分,除甲外,其余4名学生的总分是4×80=320分,
∴甲的得分是5×82-4×80=410-320=90.
D
【当堂检测】
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是 .
分析:由题意得,这(m+n)个数的平均数的和是mx+ny,
这(m+n)个数的平均数是 .
例2.在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分的一个最高分与一个最低分去掉后的平均数作为最后得分.哪一种方案更为可取?
典型例题
这时,甲的成绩比乙高.
解:按方案一计算甲、乙的最后得分为:
甲
(分)
乙
(分)
典型例题
这时,乙的成绩比甲高.
按方案二计算甲、乙的最后得分为:
甲
(分)
乙
(分)
典型例题
【当堂检测】
分析:这个班级学生的平均年龄是
3.某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
所以,他们的平均年龄约为14岁.
四、课堂总结
日常生活中,我们常用平均数表示一组数据的“平均水平”.
平均数
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
第二十章 数据的初步分析
20.2.1 数据的集中趋势
第1课时
1.掌握平均数的概念,会求一组数据的平均数
2.会用平均数解决实际生活中的问题
一、学习目标
二、新课导入
问题引入
下图表示的是甲、乙、丙三人的射击成绩,谁的成绩更好?你是怎么判断的?除了直观感觉外,我们如何用量化的数据来刻画“更好”呢?
平均数
三、概念剖析
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
例1.植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人).
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
典型例题
(2)总共植树多少棵?
(3)平均每人植树多少棵?
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1
=155(棵).
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
(3)平均每人植树 (棵).
典型例题
总结:
平均数
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
典型例题
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B.86 C.88 D.90
【当堂检测】
分析:由题意得,5名学生的总分是5×82=410分,除甲外,其余4名学生的总分是4×80=320分,
∴甲的得分是5×82-4×80=410-320=90.
D
【当堂检测】
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是 .
分析:由题意得,这(m+n)个数的平均数的和是mx+ny,
这(m+n)个数的平均数是 .
例2.在一次校园网页设计比赛中,8位评委对甲、乙两名选手的评分情况如下:
确定选手的最后得分有两种方案:一是将评委评分的平均数作为最后得分;二是将评委评分的一个最高分与一个最低分去掉后的平均数作为最后得分.哪一种方案更为可取?
典型例题
这时,甲的成绩比乙高.
解:按方案一计算甲、乙的最后得分为:
甲
(分)
乙
(分)
典型例题
这时,乙的成绩比甲高.
按方案二计算甲、乙的最后得分为:
甲
(分)
乙
(分)
典型例题
【当堂检测】
分析:这个班级学生的平均年龄是
3.某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
所以,他们的平均年龄约为14岁.
四、课堂总结
日常生活中,我们常用平均数表示一组数据的“平均水平”.
平均数
一般地,如果有n个数据, 那么, 就是这组数据的平均数,用 表示,即 .
