2023-2024学年初中数学沪科版八年级下册第16章 二次根式复习课课件(共22张PPT)
文档属性
| 名称 | 2023-2024学年初中数学沪科版八年级下册第16章 二次根式复习课课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 317.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第十六章 二次根式
复习课
一、学习目标
1.掌握二次根式的概念、二次根式的性质,并能够应用其对二次根式进行计算或化简
2.掌握二次根式的加、减、乘、除运算法则,并能够熟练地进行各种计算
3.熟悉最简二次根式和同类二次根式的定义,并能熟练地进行判断
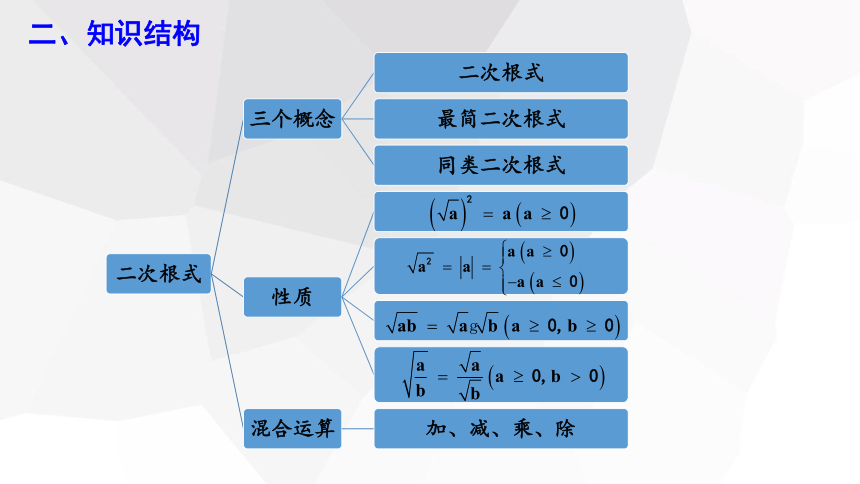
二、知识结构
三、知识梳理
1.二次根式
(1)一般地,我们把形如 的式子叫做二次根式,其中a≥0.
“ ”称为二次根号.
(2)符合
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式的二次根式叫最简二次根式.
一般地,二次根式运算结果中的根式应化成最简二次根式.
三、知识梳理
2.二次根式的性质
二次根式的非负性:
(1) ≥0 (a≥0);
(2) =a (a≥0);
(3) =a (a≥0).
三、知识梳理
3.二次根式的运算
(1)二次根式的加减运算:
可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(2)二次根式的乘除运算:
乘法:
除法:
三、知识梳理
3.二次根式的运算
(3)二次根式的混合运算:
与实数、整式和分式的混合运算一样,二次根式的运算满足分配律;满足多项式乘法法则和乘法公式.
二次根式的混合运算顺序与实数中的运算顺序一样,先算乘方,再算乘除,最后算加减,有括号的先算括号里的.
四、典型例题
例1.下列二次根式是最简二次根式的是( )
A. B. C. D.
分析: 被开方数为分数,应对分母进行有理化,化简得 .
被开方数为4,还可以进行开方,化简得2.
被开方数为8,还可以进行开方,化简得 .
C
四、典型例题
例2.若 与 互为相反数,求x+y的值.
分析: 与 均具有非负性.
解:根据题意得:
化简
解得:
∴ x + y =15+12=27.
四、典型例题
归纳总结:
对于二次根式 ,有两个非负性:一是a≥0,二是 ≥0,这两个非负性在解二次根式有关题目时经常用到.二次根式 的值是非负数,是一种常见的隐含条件,另外绝对值、偶次幂也有非负性,在题目中常常作为隐含条件,一定要引起重视.
【当堂检测】
1.在 中最简二次根式的个数是( )
A.1个 B.2个 C.3个 D.4个
A
【当堂检测】
2.能使二次根式 有意义的实数x的值有( )
A.0个 B.1个 C.2个 D.无数个
B
分析:∵-(x-2) ≥0, (x-2) ≤0,
∴使二次根式 有意义的实数x的值只能为2.
四、典型例题
例3.已知 ,比较a、b的大小.
解:
分析: ,故该题选择商值比较法比较方便
所以a=b
四、典型例题
归纳总结:
1.根据数的特点,选择比较大小的方法;
2.完全平方和平方差公式在比较大小中也常用到.
【当堂检测】
3.在 , ,3 ,四个数中,最小的数是( )
A. B.
C.3 D.
D
提示:以3为分界点,逐个与3比较大小,比3小的数据在进行比较得出最终结果
四、典型例题
例4.计算:
(1) ; (2)
解:(1)原式=
(2)原式=
四、典型例题
例4.计算:
(3) ; (4)
(3)原式=
(4)原式=
四、典型例题
归纳总结:
在二次根式的混合运算中,应熟练运用二次根式的乘除法和加减法法则,掌握二次根式混合运算的顺序,在计算时要观察式子的特征,整式的乘法公式和运算律同样适用.
【当堂检测】
4.下列运算正确的是( )
A. B.
C. D.
D
5.计算:
(1) ; (2)
解:(1)原式=
(2)原式=
【当堂检测】
5.计算:
(3) ; (4)
(3)原式=
(4)原式=
【当堂检测】
五、课堂总结
1.一般地,我们把形如 的式子叫做二次根式,其中a≥0.
2.符合
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式的二次根式叫最简二次根式.
一般地,二次根式运算结果中的根式应化成最简二次根式.
3.二次根式的混合运算:
先算乘方(或开方),再算乘除,最后算加减,有括号时先算括号里面的;能利用运算律或乘法公式进行运算的,可适当改变运算顺序进行简便运算.
第十六章 二次根式
复习课
一、学习目标
1.掌握二次根式的概念、二次根式的性质,并能够应用其对二次根式进行计算或化简
2.掌握二次根式的加、减、乘、除运算法则,并能够熟练地进行各种计算
3.熟悉最简二次根式和同类二次根式的定义,并能熟练地进行判断
二、知识结构
三、知识梳理
1.二次根式
(1)一般地,我们把形如 的式子叫做二次根式,其中a≥0.
“ ”称为二次根号.
(2)符合
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式的二次根式叫最简二次根式.
一般地,二次根式运算结果中的根式应化成最简二次根式.
三、知识梳理
2.二次根式的性质
二次根式的非负性:
(1) ≥0 (a≥0);
(2) =a (a≥0);
(3) =a (a≥0).
三、知识梳理
3.二次根式的运算
(1)二次根式的加减运算:
可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(2)二次根式的乘除运算:
乘法:
除法:
三、知识梳理
3.二次根式的运算
(3)二次根式的混合运算:
与实数、整式和分式的混合运算一样,二次根式的运算满足分配律;满足多项式乘法法则和乘法公式.
二次根式的混合运算顺序与实数中的运算顺序一样,先算乘方,再算乘除,最后算加减,有括号的先算括号里的.
四、典型例题
例1.下列二次根式是最简二次根式的是( )
A. B. C. D.
分析: 被开方数为分数,应对分母进行有理化,化简得 .
被开方数为4,还可以进行开方,化简得2.
被开方数为8,还可以进行开方,化简得 .
C
四、典型例题
例2.若 与 互为相反数,求x+y的值.
分析: 与 均具有非负性.
解:根据题意得:
化简
解得:
∴ x + y =15+12=27.
四、典型例题
归纳总结:
对于二次根式 ,有两个非负性:一是a≥0,二是 ≥0,这两个非负性在解二次根式有关题目时经常用到.二次根式 的值是非负数,是一种常见的隐含条件,另外绝对值、偶次幂也有非负性,在题目中常常作为隐含条件,一定要引起重视.
【当堂检测】
1.在 中最简二次根式的个数是( )
A.1个 B.2个 C.3个 D.4个
A
【当堂检测】
2.能使二次根式 有意义的实数x的值有( )
A.0个 B.1个 C.2个 D.无数个
B
分析:∵-(x-2) ≥0, (x-2) ≤0,
∴使二次根式 有意义的实数x的值只能为2.
四、典型例题
例3.已知 ,比较a、b的大小.
解:
分析: ,故该题选择商值比较法比较方便
所以a=b
四、典型例题
归纳总结:
1.根据数的特点,选择比较大小的方法;
2.完全平方和平方差公式在比较大小中也常用到.
【当堂检测】
3.在 , ,3 ,四个数中,最小的数是( )
A. B.
C.3 D.
D
提示:以3为分界点,逐个与3比较大小,比3小的数据在进行比较得出最终结果
四、典型例题
例4.计算:
(1) ; (2)
解:(1)原式=
(2)原式=
四、典型例题
例4.计算:
(3) ; (4)
(3)原式=
(4)原式=
四、典型例题
归纳总结:
在二次根式的混合运算中,应熟练运用二次根式的乘除法和加减法法则,掌握二次根式混合运算的顺序,在计算时要观察式子的特征,整式的乘法公式和运算律同样适用.
【当堂检测】
4.下列运算正确的是( )
A. B.
C. D.
D
5.计算:
(1) ; (2)
解:(1)原式=
(2)原式=
【当堂检测】
5.计算:
(3) ; (4)
(3)原式=
(4)原式=
【当堂检测】
五、课堂总结
1.一般地,我们把形如 的式子叫做二次根式,其中a≥0.
2.符合
①被开方数不含分母;
②被开方数中不含能开得尽方的因数或因式的二次根式叫最简二次根式.
一般地,二次根式运算结果中的根式应化成最简二次根式.
3.二次根式的混合运算:
先算乘方(或开方),再算乘除,最后算加减,有括号时先算括号里面的;能利用运算律或乘法公式进行运算的,可适当改变运算顺序进行简便运算.
