9.2.2 分式的加减 第2课时 课件(共26张PPT) 2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 9.2.2 分式的加减 第2课时 课件(共26张PPT) 2023-2024学年初中数学沪科版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第 9 章 分式
9.2.2 分式的加减
第 2 课时
一、学习目标
1.理解分式加减的法则,并能熟练地进行分式加减运算;
2.类比数与整式的加、减、乘、除、乘方混合运算,理解分式
的混合运算.
二、新课导入
甲地到乙地有两条路,每条路都是3km,其中第一条是平路,第二条有
1km的上坡路,2km的下坡路,小丽在上坡路骑车速度为v km/h,在平路上的
骑车速度为2v km/h,在下坡路速度为3v km/h.她走哪条路更快?
第一路所用时间:
第二条路所用时间:
h
h
两个式子无法直接比较,我们该怎么样计算 呢?
三、概念剖析
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算.
我们已经学过了分数的加减运算,你还记得吗?
+ =
- =
+ = + =
- = - =
说一说分数的加减法则.
你能类比分数的加减法,得出分式的加减法则吗?
三、概念剖析
归纳总结
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
分式的加减法则
上述法则可用式子表示为
± =
± = ± =
四、典型例题
例1 计算:(1)
解:(1)原式=
=
(2)
(2)原式=
=
=
注意:y-x=-(x-y).
四、典型例题
例1 计算:(3)
解:原式=
注意:结果要化为最简分式!
把分子看成一个整体,先用括号括起来!
=
=
=
四、典型例题
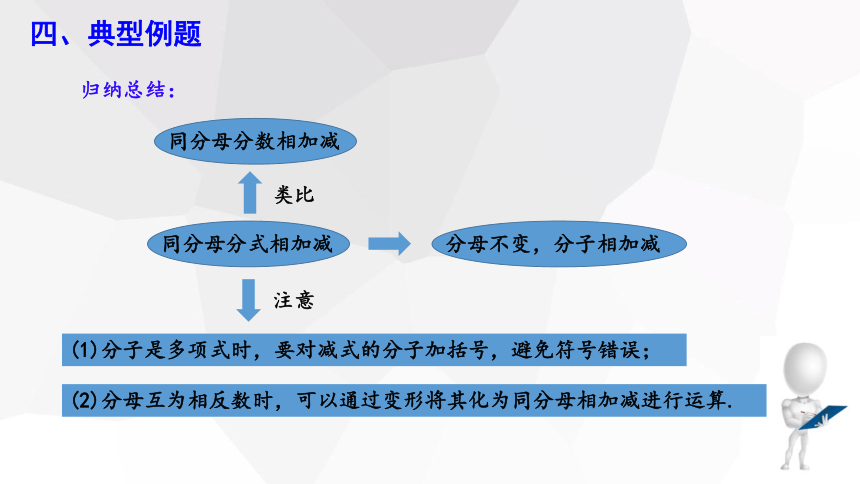
归纳总结:
同分母分数相加减
同分母分式相加减
类比
注意
分母不变,分子相加减
(1)分子是多项式时,要对减式的分子加括号,避免符号错误;
(2)分母互为相反数时,可以通过变形将其化为同分母相加减进行运算.
1.计算.
【当堂检测】
(2)
(1)
=
解:(1)原式=
=1
(2)原式=
=
=x+2
【当堂检测】
(3)
=
(3)原式=
=
四、典型例题
例2 计算:(1)
解:(1)原式=
=
=
先通分,变为同分母的分式
四、典型例题
例2 计算:(2)
解:(2)原式=
=
=
=
或
四、典型例题
例2 计算:(3)
解:(3)原式=
=
=
=
注意:分母是多项式
可以考虑先分解因式
【当堂检测】
2.计算
(2)
(1)
=
解:(1)原式=
=-1
=
(2)原式=
【当堂检测】
2.计算
(3)
=
(3)原式=
三、典型例题
例3 计算:
解:原式=
观察计算的步骤,分式
与分数的混合运算的运算
顺序相同吗?
三、典型例题
总结:分式与分数有相同的混合运算顺序:
先乘方,再乘除,然后加减
(1)运算顺序:先乘方,再乘除,然后加减;
对于一般的分式混合运算:
(2)计算结果要化为最简分式.
如果有括号,先进行括号里的运算.
【当堂检测】
3.化简: 的结果是 .
解析:原式
m
【当堂检测】
4.计算:
解:原式=
例4 计算:(1)
三、典型例题
解:(1)原式=
=-2(3+m)
=-6-2m
例4 计算:(2)
三、典型例题
解:(2)原式=
四、典型例题
总结:对于分式的分子、分母是多项式时的运算:
1.将各分式的分子、分母分解因式后,再进行计算;
2.注意处理好每一步运算中遇到的符号;
3.计算结果要化为最简分式.
【当堂检测】
5.计算:(1)
解:原式=
【当堂检测】
5.计算.(2)
解:原式=
五、课堂总结
1.分式加减运算的方法思路:
分子相加减时,如果分子是一个多项式,要将分子看成一个整体,
先用括号括起来,再运算,可减少出现符号错误.
分式加减运算的结果要约分,化为最简分式(或整式).
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
五、课堂总结
2.分式的混合运算的注意点:
1.有理数的运算律对于分式运算同样适用;
2.注意运算顺序,运算结果一定要化为最简分式或整式;
3.分母或分子是负数,要把负号提到分式前面;
4.分子、分母是是多项式时,可先将分子分母分解因式再计算.
第 9 章 分式
9.2.2 分式的加减
第 2 课时
一、学习目标
1.理解分式加减的法则,并能熟练地进行分式加减运算;
2.类比数与整式的加、减、乘、除、乘方混合运算,理解分式
的混合运算.
二、新课导入
甲地到乙地有两条路,每条路都是3km,其中第一条是平路,第二条有
1km的上坡路,2km的下坡路,小丽在上坡路骑车速度为v km/h,在平路上的
骑车速度为2v km/h,在下坡路速度为3v km/h.她走哪条路更快?
第一路所用时间:
第二条路所用时间:
h
h
两个式子无法直接比较,我们该怎么样计算 呢?
三、概念剖析
从上面的问题可知,为讨论数量关系,有时需要进行分式的加减运算.
我们已经学过了分数的加减运算,你还记得吗?
+ =
- =
+ = + =
- = - =
说一说分数的加减法则.
你能类比分数的加减法,得出分式的加减法则吗?
三、概念剖析
归纳总结
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
分式的加减法则
上述法则可用式子表示为
± =
± = ± =
四、典型例题
例1 计算:(1)
解:(1)原式=
=
(2)
(2)原式=
=
=
注意:y-x=-(x-y).
四、典型例题
例1 计算:(3)
解:原式=
注意:结果要化为最简分式!
把分子看成一个整体,先用括号括起来!
=
=
=
四、典型例题
归纳总结:
同分母分数相加减
同分母分式相加减
类比
注意
分母不变,分子相加减
(1)分子是多项式时,要对减式的分子加括号,避免符号错误;
(2)分母互为相反数时,可以通过变形将其化为同分母相加减进行运算.
1.计算.
【当堂检测】
(2)
(1)
=
解:(1)原式=
=1
(2)原式=
=
=x+2
【当堂检测】
(3)
=
(3)原式=
=
四、典型例题
例2 计算:(1)
解:(1)原式=
=
=
先通分,变为同分母的分式
四、典型例题
例2 计算:(2)
解:(2)原式=
=
=
=
或
四、典型例题
例2 计算:(3)
解:(3)原式=
=
=
=
注意:分母是多项式
可以考虑先分解因式
【当堂检测】
2.计算
(2)
(1)
=
解:(1)原式=
=-1
=
(2)原式=
【当堂检测】
2.计算
(3)
=
(3)原式=
三、典型例题
例3 计算:
解:原式=
观察计算的步骤,分式
与分数的混合运算的运算
顺序相同吗?
三、典型例题
总结:分式与分数有相同的混合运算顺序:
先乘方,再乘除,然后加减
(1)运算顺序:先乘方,再乘除,然后加减;
对于一般的分式混合运算:
(2)计算结果要化为最简分式.
如果有括号,先进行括号里的运算.
【当堂检测】
3.化简: 的结果是 .
解析:原式
m
【当堂检测】
4.计算:
解:原式=
例4 计算:(1)
三、典型例题
解:(1)原式=
=-2(3+m)
=-6-2m
例4 计算:(2)
三、典型例题
解:(2)原式=
四、典型例题
总结:对于分式的分子、分母是多项式时的运算:
1.将各分式的分子、分母分解因式后,再进行计算;
2.注意处理好每一步运算中遇到的符号;
3.计算结果要化为最简分式.
【当堂检测】
5.计算:(1)
解:原式=
【当堂检测】
5.计算.(2)
解:原式=
五、课堂总结
1.分式加减运算的方法思路:
分子相加减时,如果分子是一个多项式,要将分子看成一个整体,
先用括号括起来,再运算,可减少出现符号错误.
分式加减运算的结果要约分,化为最简分式(或整式).
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
五、课堂总结
2.分式的混合运算的注意点:
1.有理数的运算律对于分式运算同样适用;
2.注意运算顺序,运算结果一定要化为最简分式或整式;
3.分母或分子是负数,要把负号提到分式前面;
4.分子、分母是是多项式时,可先将分子分母分解因式再计算.
