10.2 平行线的判定 第1课时 课件 (共21张PPT)2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 10.2 平行线的判定 第1课时 课件 (共21张PPT)2023-2024学年初中数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 710.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:16:18 | ||
图片预览








文档简介
(共21张PPT)
第 10 章 相交线、平行线与平移
10.2 平行线的判定
第 1 课时
一、学习目标
1.知道平行线的概念,探究平行线的基本事实;
2.知道第一个平行线的判定方法;
3.会识别图形中的同位角、内错角和同旁内角.(重点)
二、新课导入
很早以前,人们就把滑雪作为雪上运动的一种方式.
滑雪运动关键的是要保持两只雪橇板的平行.
三、概念剖析
(一)平行线的概念
在同一平面内,不相交的两条直线叫平行线.(定义)
如图,两条直线AB和CD平行,记作“AB∥CD”,
读作“AB平行于CD”.
A
C
D
B
三、概念剖析
注意:平行线的定义包含三层意思:
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
(2)“不相交”就是说两条直线没有交点;
(1)“在同一平面内”是前提条件;
典型例题
例1.判断下列说法是否正确,并说明理由.
错误,前提是同一平面内不相交的两条直线.
(1)两条不相交的直线叫做平行线;
错误,没有公共点的两条线段所在直线可能相交.
(2)没有公共点的两条线段一定平行;
(3)同一平面内,两条直线的位置关系有三种,分别是相交、平行、垂直;
错误,在同一平面内,两条直线的位置关系有两种,分别是相交、平行.
【当堂检测】
1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线;
B.在同一平面内,不相交的两条线段是平行线;
C.在同一平面内,两条直线的位置关系不相交就平行;
D.不相交的两条直线是平行线
C
三、概念剖析
(二)平行线的基本事实和判定
a
P
a
P
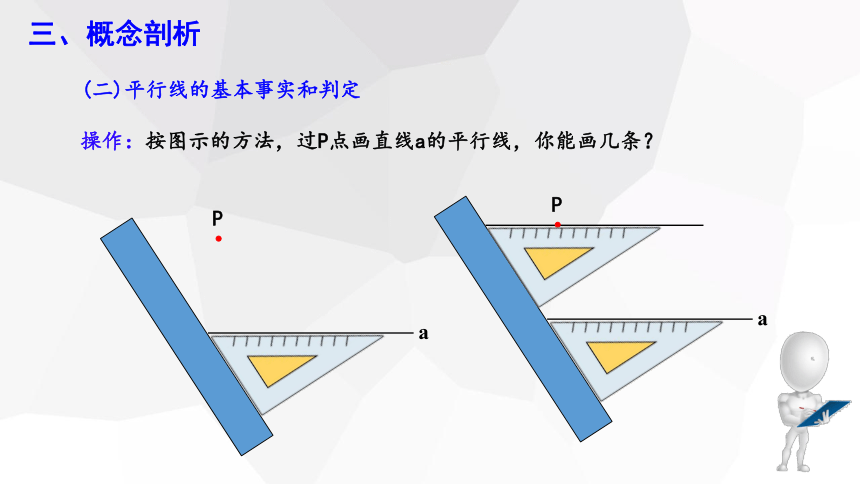
操作:按图示的方法,过P点画直线a的平行线,你能画几条?
三、概念剖析
通过观察和画图,可以发现一个基本事实:
·
P
a
经过直线外一点,有且只有一条直线平行于这条直线.
三、概念剖析
观察:如图,如果直线a∥c,b∥c,想一想a与b有怎样的位置关系?
a
b
c
平行
我们来了解一下为什么a与b一定平行,
a
b
c
P
假如a与b存在交点P,
那么过P点,就有两条直线(直线a、直线b)平行于直线c.
与基本事实不符,故直线a与b平行.
三、概念剖析
归纳总结
平行线的一个判定方法;
如果两条直线和第三条直线平行,那么这两条直线平行.
即如果a∥c,b∥c,那么直线a∥b.
典型例题
例2.完成下列推理,并在括号内注明理由.
(1)如图1所示,因为AB // DE,BC // DE(已知).所以A,B,C三点
( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以____∥_____
( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,那么这两条直线也互相平行
【当堂检测】
2.如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
解:因为 a ∥b,b∥c,所以 a ∥c;
( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,所以 a ∥d.
( )
a
b
c
d
三、概念剖析
(三)同位角、内错角、和同旁内角
b
c
a
(
(
(
(
1
2
3
4
(
(
(
(
5
6
7
8
要研究同一平面内直线a和b是否平行,通常添加一条
“基准线”,通过它与直线a和b的夹角来讨论.
如图,两条直线a和b被第三条直线c所截,
直线c的同旁,具有这样位置关系的一对角叫做同位角.
其中∠2和∠6,分别在直线a和b的同一侧,并且位于
三、概念剖析
b
c
a
(
(
(
(
1
2
3
4
(
(
(
(
5
6
7
8
同样,∠8和∠2都在直线a和b之间,并且位于直线c
的两旁,具有这样位置关系的一对角叫做内错角.
∠7和∠2都在直线a和b之间,并且位于直线c的同旁,
具有这样位置关系的一对角叫做同旁内角.
三、概念剖析
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的_____ 形如字母___
“F”
同旁
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
典型例题
解:∠1和∠2是同位角,是由直线CD、FE被AB截成的;
例3.如图,∠ 1和∠ 2是什么角?∠ 2和∠ 3呢?∠ 4和∠ 5呢?它们分别是由哪两条直线被哪一条直线截成的?
A
B
C
D
E
F
⌒
3
⌒
2
A
B
C
D
E
F
⌒
1
⌒
2
A
B
C
D
E
F
⌒
4
⌒
5
G
∠2和∠3是内错角,是由直线AB、CD被EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被CD截成的.
【当堂检测】
3.填空题:
(1)∠BAD与∠ CDA是直线 和 被 所截,构成的同旁内角.
(2)∠ 1和∠ 2是直线 和 被 所截,构成的内错角.
(3)∠ 3和∠ 4是直线 和 被 所截,构成的内错角.
(4) ∠ DCE与∠ ABC是直线 和 被 所截,构成的同位角.
AB
CD
AD
AD
BC
AC
AB
CD
AC
AB
CD
BE
⌒
⌒
A
B
C
D
⌒
⌒
B
C
D
A
E
⌒
⌒
A
B
C
D
1
2
⌒
⌒
A
B
C
D
3
4
【当堂检测】
4.指出下列各图中∠1与∠2的位置关系.
同旁内角
同位角
内错角
同旁内角
内错角
1
2
1
2
1
2
1
2
2
1
2
1
同位角
四、课堂总结
1.平行线的定义:
2.平行线的表示方法:
·
·
A
B
·
·
C
D
m
n
m//n AB//CD
3.平行线的基本事实:
经过直线外一点,有且只有一条直线与这条直线平行;
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
4.平行线的一个判定方法:
在同一平面内,不相交的两条直线叫做平行线.
四、课堂总结
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的同旁, 在截线的同侧 形如字母“F”
在两条被截直线的之间, 在截线的两侧 形如字母“Z”
在两条被截直线的之间, 在截线的同侧 形如字母“U”
内错角
同旁内角
第 10 章 相交线、平行线与平移
10.2 平行线的判定
第 1 课时
一、学习目标
1.知道平行线的概念,探究平行线的基本事实;
2.知道第一个平行线的判定方法;
3.会识别图形中的同位角、内错角和同旁内角.(重点)
二、新课导入
很早以前,人们就把滑雪作为雪上运动的一种方式.
滑雪运动关键的是要保持两只雪橇板的平行.
三、概念剖析
(一)平行线的概念
在同一平面内,不相交的两条直线叫平行线.(定义)
如图,两条直线AB和CD平行,记作“AB∥CD”,
读作“AB平行于CD”.
A
C
D
B
三、概念剖析
注意:平行线的定义包含三层意思:
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
(2)“不相交”就是说两条直线没有交点;
(1)“在同一平面内”是前提条件;
典型例题
例1.判断下列说法是否正确,并说明理由.
错误,前提是同一平面内不相交的两条直线.
(1)两条不相交的直线叫做平行线;
错误,没有公共点的两条线段所在直线可能相交.
(2)没有公共点的两条线段一定平行;
(3)同一平面内,两条直线的位置关系有三种,分别是相交、平行、垂直;
错误,在同一平面内,两条直线的位置关系有两种,分别是相交、平行.
【当堂检测】
1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线;
B.在同一平面内,不相交的两条线段是平行线;
C.在同一平面内,两条直线的位置关系不相交就平行;
D.不相交的两条直线是平行线
C
三、概念剖析
(二)平行线的基本事实和判定
a
P
a
P
操作:按图示的方法,过P点画直线a的平行线,你能画几条?
三、概念剖析
通过观察和画图,可以发现一个基本事实:
·
P
a
经过直线外一点,有且只有一条直线平行于这条直线.
三、概念剖析
观察:如图,如果直线a∥c,b∥c,想一想a与b有怎样的位置关系?
a
b
c
平行
我们来了解一下为什么a与b一定平行,
a
b
c
P
假如a与b存在交点P,
那么过P点,就有两条直线(直线a、直线b)平行于直线c.
与基本事实不符,故直线a与b平行.
三、概念剖析
归纳总结
平行线的一个判定方法;
如果两条直线和第三条直线平行,那么这两条直线平行.
即如果a∥c,b∥c,那么直线a∥b.
典型例题
例2.完成下列推理,并在括号内注明理由.
(1)如图1所示,因为AB // DE,BC // DE(已知).所以A,B,C三点
( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以____∥_____
( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,那么这两条直线也互相平行
【当堂检测】
2.如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
解:因为 a ∥b,b∥c,所以 a ∥c;
( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,所以 a ∥d.
( )
a
b
c
d
三、概念剖析
(三)同位角、内错角、和同旁内角
b
c
a
(
(
(
(
1
2
3
4
(
(
(
(
5
6
7
8
要研究同一平面内直线a和b是否平行,通常添加一条
“基准线”,通过它与直线a和b的夹角来讨论.
如图,两条直线a和b被第三条直线c所截,
直线c的同旁,具有这样位置关系的一对角叫做同位角.
其中∠2和∠6,分别在直线a和b的同一侧,并且位于
三、概念剖析
b
c
a
(
(
(
(
1
2
3
4
(
(
(
(
5
6
7
8
同样,∠8和∠2都在直线a和b之间,并且位于直线c
的两旁,具有这样位置关系的一对角叫做内错角.
∠7和∠2都在直线a和b之间,并且位于直线c的同旁,
具有这样位置关系的一对角叫做同旁内角.
三、概念剖析
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的______ 形如字母___
在两条被截直线的______, 在截线的_____ 形如字母___
“F”
同旁
同侧
内错角
之间
两侧
“Z”
同旁内角
之间
同侧
“U”
典型例题
解:∠1和∠2是同位角,是由直线CD、FE被AB截成的;
例3.如图,∠ 1和∠ 2是什么角?∠ 2和∠ 3呢?∠ 4和∠ 5呢?它们分别是由哪两条直线被哪一条直线截成的?
A
B
C
D
E
F
⌒
3
⌒
2
A
B
C
D
E
F
⌒
1
⌒
2
A
B
C
D
E
F
⌒
4
⌒
5
G
∠2和∠3是内错角,是由直线AB、CD被EF截成的;
∠4和∠5是同旁内角,是由直线AB 、EF被CD截成的.
【当堂检测】
3.填空题:
(1)∠BAD与∠ CDA是直线 和 被 所截,构成的同旁内角.
(2)∠ 1和∠ 2是直线 和 被 所截,构成的内错角.
(3)∠ 3和∠ 4是直线 和 被 所截,构成的内错角.
(4) ∠ DCE与∠ ABC是直线 和 被 所截,构成的同位角.
AB
CD
AD
AD
BC
AC
AB
CD
AC
AB
CD
BE
⌒
⌒
A
B
C
D
⌒
⌒
B
C
D
A
E
⌒
⌒
A
B
C
D
1
2
⌒
⌒
A
B
C
D
3
4
【当堂检测】
4.指出下列各图中∠1与∠2的位置关系.
同旁内角
同位角
内错角
同旁内角
内错角
1
2
1
2
1
2
1
2
2
1
2
1
同位角
四、课堂总结
1.平行线的定义:
2.平行线的表示方法:
·
·
A
B
·
·
C
D
m
n
m//n AB//CD
3.平行线的基本事实:
经过直线外一点,有且只有一条直线与这条直线平行;
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
4.平行线的一个判定方法:
在同一平面内,不相交的两条直线叫做平行线.
四、课堂总结
角的名称 位置特征 基本图形 图形结构特征
同位角 在两条被截直线的同旁, 在截线的同侧 形如字母“F”
在两条被截直线的之间, 在截线的两侧 形如字母“Z”
在两条被截直线的之间, 在截线的同侧 形如字母“U”
内错角
同旁内角
