2023-2024学年初中数学沪科版七年级下册第7章 一元一次不等式和不等式组复习课课件(共26张PPT)
文档属性
| 名称 | 2023-2024学年初中数学沪科版七年级下册第7章 一元一次不等式和不等式组复习课课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第 7 章 一元一次不等式与不等式组
复习课
一、学习目标
1.进一步理解不等式的概念及其基本性质;
2.掌握一元一次不等式和一元一次不等式组的概念与解法;(重点)
3.能运用一元一次不等式(组)解决相关的数学问题和简单的
实际问题.
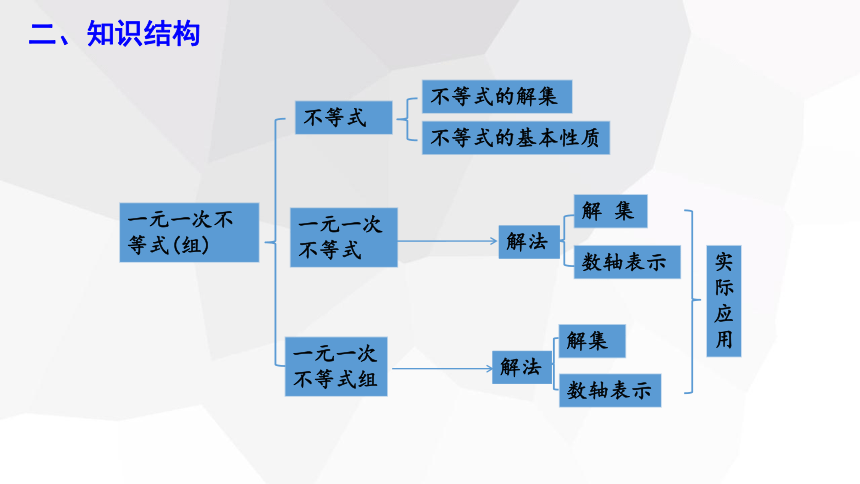
二、知识结构
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
三、知识梳理
1.不等式的有关概念
不等号有:>、≥、<、≤或≠.
用不等式号表示不等关系的式子叫做不等式.
三、知识梳理
2.不等式的基本性质
性质1:如果a>b,那么a+c>b+c,且 a-c>b-c.
不等式还具有传递性:如果a>b,b>c,那么a>c.
性质2:如果a>b,c>0,那么ac > bc , > .
性质3:如果a>b,c<0,那么ac < bc , < .
三、知识梳理
3.一元一次不等式的相关概念
(1)一元一次不等式的评判标准是:
①只含有一个未知数;②未知数的次数是1;③不等式两边都是整式.
(2)使不等式成立的未知数的值叫做不等式的解,这些解的全体称为这个不
等式的解集,求不等式解集的过程叫解不等式.
三、知识梳理
4.一元一次不等式组的概念
这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.
一元一次不等式组:
一元一次不等式组的解集:
几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次
不等式组.
三、知识梳理
5.解一元一次不等式
①去分母;②去括号;③移项;
④合并同类项;
⑤将未知数系数化为1.
注意:在上面步骤①和⑤中,如果乘数或除数是负数,那么在利用不等式
的基本性质3时,一定要改变不等号的方向.
解一元一次不等式的一般步骤:
三、知识梳理
6.解一元一次不等式组
1.分别求出不等式组中各个不等式的解集;
2.利用数轴求出这些不等式的解集的公共部分.
三、知识梳理
7.用数轴表示一元一次不等式(组)的解集
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
a
b
a
b
a
b
a
b
三、知识梳理
8.利用一元一次不等式(组)解决实际问题
1.根据题意,适当设出未知数;
2.找出题中能概括数量间关系的不等关系;
3.用未知数表示不等关系中的数量;
4.列出不等式(组)并求出其解集;
5.检验并根据实际问题的要求写出符合题意的解或解集,并写出答案.
四、典型例题
D
解析:根据不等式的性质1,不等式的两边都加上(或减去)同一数或同
一个整式,不等号的方向不变.故A、B正确.
根据不等式的性质2,不等式的两边都乘(或除以)同一个正数,不等号
的方向不变.故C正确.
根据不等式的基本性质3,不等式的两边同时乘(或除以)同一个负数,
不等号的方向改变,故D选项错误,应为-4a<-4b.
例1.若a>b,则下列结论错误的是( )
A.a-5>b-5 B.5+a>b+5
C. D.-4a>-4b
四、典型例题
归纳总结:不等式变形的两点注意:
(1)一般要把不等式的右边化成常数,左边化成只含有未知数的形式,
(2)应用不等式的基本性质3时,要改变不等号的方向.
【当堂检测】
1. 已知aA.3a<3b B.-3a<-3b
C.a-3B
四、典型例题
例2. 解不等式 ,并把它的解集表示在数轴上.
解:
去分母,得 2(4+x)-6<3x.
去括号,得 8+2x-6<3x.
移项、合并同类项,得 -x<-2.
x的系数化为1,得 x>2.
这个不等式的解集在数轴上表示如下:
2
1
0
3
4
四、典型例题
归纳总结:先求出不等式的解集,然后根据“大于向右画,小于向左画,
含等号用实心圆点,不含等号用空心圆圈”的原则在数轴上表示解集.
解一元一次不等式的几点注意:
(1)去分母时不要漏乘常数项;
(2)移项要变号;
(3)系数化为1时,若系数为负数,要改变不等号的方向.
【当堂检测】
3.已知关于x的方程2x+4=m-x的解为负数,则m的取值范围是 .
m<4
2. 解不等式 ,它的解集为 ,
y≤
你能将它在数轴上表示吗?
0
四、典型例题
例3.解不等式组 ,利用数轴确定不等式组的解集.
解:
解不等式5x+1>3(x+1),得x>1,
解不等式x-3≤7-x,得x≤5,
所以不等式组的解集为1<x≤5.
两个不等式的解集表示在数轴上如下:
0
1
2
3
4
5
四、典型例题
例4.解不等式组:
-2x+1>3, ①
2x+3≥5, ②
解:由①得:x<-1,
由②得:x≥1,
因此原不等式组无解.
归纳总结:解一元一次不等式组的方法:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴表示出不等式组中的各个不等式的解集;
(3)在数轴上找出各个不等式的解集的公共部分,即求出了这个不等式组的
解集.
四、典型例题
【当堂检测】
5.若关于x不等式组 有解,则m的取值范围为( )
A.m> B.m≤ C.m> D.m≤
C
4.使不等式x-1≥2与3x-7<8同时成立的x的整数值是 .
3或4
【当堂检测】
6.直接写出下列不等式的解集.
x≥4
x>-4
(1)
x<-3
x≤-2
(2)
x>-1
x<5
(3)
x>-4
x<-5
(4)
x≥4
x<-3
-1<x<5
无解
四、典型例题
例5.某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、
6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为x株,依题意,得
解得x≥120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
四、典型例题
归纳总结:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个
环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),
然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问
题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
【当堂检测】
7.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分
4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5因为x是整数,所以x=6,7,8.
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
五、课堂总结
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
第 7 章 一元一次不等式与不等式组
复习课
一、学习目标
1.进一步理解不等式的概念及其基本性质;
2.掌握一元一次不等式和一元一次不等式组的概念与解法;(重点)
3.能运用一元一次不等式(组)解决相关的数学问题和简单的
实际问题.
二、知识结构
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
三、知识梳理
1.不等式的有关概念
不等号有:>、≥、<、≤或≠.
用不等式号表示不等关系的式子叫做不等式.
三、知识梳理
2.不等式的基本性质
性质1:如果a>b,那么a+c>b+c,且 a-c>b-c.
不等式还具有传递性:如果a>b,b>c,那么a>c.
性质2:如果a>b,c>0,那么ac > bc , > .
性质3:如果a>b,c<0,那么ac < bc , < .
三、知识梳理
3.一元一次不等式的相关概念
(1)一元一次不等式的评判标准是:
①只含有一个未知数;②未知数的次数是1;③不等式两边都是整式.
(2)使不等式成立的未知数的值叫做不等式的解,这些解的全体称为这个不
等式的解集,求不等式解集的过程叫解不等式.
三、知识梳理
4.一元一次不等式组的概念
这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.
一元一次不等式组:
一元一次不等式组的解集:
几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次
不等式组.
三、知识梳理
5.解一元一次不等式
①去分母;②去括号;③移项;
④合并同类项;
⑤将未知数系数化为1.
注意:在上面步骤①和⑤中,如果乘数或除数是负数,那么在利用不等式
的基本性质3时,一定要改变不等号的方向.
解一元一次不等式的一般步骤:
三、知识梳理
6.解一元一次不等式组
1.分别求出不等式组中各个不等式的解集;
2.利用数轴求出这些不等式的解集的公共部分.
三、知识梳理
7.用数轴表示一元一次不等式(组)的解集
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
a
b
a
b
a
b
a
b
三、知识梳理
8.利用一元一次不等式(组)解决实际问题
1.根据题意,适当设出未知数;
2.找出题中能概括数量间关系的不等关系;
3.用未知数表示不等关系中的数量;
4.列出不等式(组)并求出其解集;
5.检验并根据实际问题的要求写出符合题意的解或解集,并写出答案.
四、典型例题
D
解析:根据不等式的性质1,不等式的两边都加上(或减去)同一数或同
一个整式,不等号的方向不变.故A、B正确.
根据不等式的性质2,不等式的两边都乘(或除以)同一个正数,不等号
的方向不变.故C正确.
根据不等式的基本性质3,不等式的两边同时乘(或除以)同一个负数,
不等号的方向改变,故D选项错误,应为-4a<-4b.
例1.若a>b,则下列结论错误的是( )
A.a-5>b-5 B.5+a>b+5
C. D.-4a>-4b
四、典型例题
归纳总结:不等式变形的两点注意:
(1)一般要把不等式的右边化成常数,左边化成只含有未知数的形式,
(2)应用不等式的基本性质3时,要改变不等号的方向.
【当堂检测】
1. 已知a
C.a-3
四、典型例题
例2. 解不等式 ,并把它的解集表示在数轴上.
解:
去分母,得 2(4+x)-6<3x.
去括号,得 8+2x-6<3x.
移项、合并同类项,得 -x<-2.
x的系数化为1,得 x>2.
这个不等式的解集在数轴上表示如下:
2
1
0
3
4
四、典型例题
归纳总结:先求出不等式的解集,然后根据“大于向右画,小于向左画,
含等号用实心圆点,不含等号用空心圆圈”的原则在数轴上表示解集.
解一元一次不等式的几点注意:
(1)去分母时不要漏乘常数项;
(2)移项要变号;
(3)系数化为1时,若系数为负数,要改变不等号的方向.
【当堂检测】
3.已知关于x的方程2x+4=m-x的解为负数,则m的取值范围是 .
m<4
2. 解不等式 ,它的解集为 ,
y≤
你能将它在数轴上表示吗?
0
四、典型例题
例3.解不等式组 ,利用数轴确定不等式组的解集.
解:
解不等式5x+1>3(x+1),得x>1,
解不等式x-3≤7-x,得x≤5,
所以不等式组的解集为1<x≤5.
两个不等式的解集表示在数轴上如下:
0
1
2
3
4
5
四、典型例题
例4.解不等式组:
-2x+1>3, ①
2x+3≥5, ②
解:由①得:x<-1,
由②得:x≥1,
因此原不等式组无解.
归纳总结:解一元一次不等式组的方法:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴表示出不等式组中的各个不等式的解集;
(3)在数轴上找出各个不等式的解集的公共部分,即求出了这个不等式组的
解集.
四、典型例题
【当堂检测】
5.若关于x不等式组 有解,则m的取值范围为( )
A.m> B.m≤ C.m> D.m≤
C
4.使不等式x-1≥2与3x-7<8同时成立的x的整数值是 .
3或4
【当堂检测】
6.直接写出下列不等式的解集.
x≥4
x>-4
(1)
x<-3
x≤-2
(2)
x>-1
x<5
(3)
x>-4
x<-5
(4)
x≥4
x<-3
-1<x<5
无解
四、典型例题
例5.某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、
6元.若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为x株,依题意,得
解得x≥120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
四、典型例题
归纳总结:解不等式的应用问题的步骤包括审、设、列、解、找、答这几个
环节,而在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),
然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问
题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
【当堂检测】
7.一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分
4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
解:
设小朋友总共x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
五、课堂总结
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
