第9章 分式复习课课件 24张PPT 2023-2024学年初中数学沪科版七年级下册
文档属性
| 名称 | 第9章 分式复习课课件 24张PPT 2023-2024学年初中数学沪科版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:26:23 | ||
图片预览








文档简介
(共24张PPT)
第 9 章 分式
复习课
一、学习目标
1.巩固分式的相关概念及其基本性质;
2.能熟练地进行分式的相关运算,解分式方程;
3.能用分式方程解决相关数学问题与生活中的实际问题.
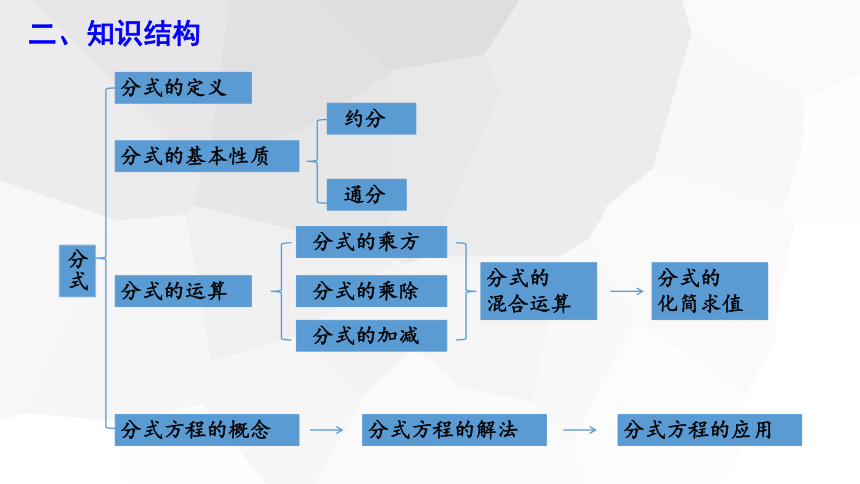
二、知识结构
分式
分式的定义
分式的基本性质
约分
通分
分式的运算
分式的乘方
分式的乘除
分式的加减
分式的
混合运算
分式的
化简求值
分式方程的概念
分式方程的解法
分式方程的应用
三、知识梳理
1.分式的概念与基本性质
(1)分式的概念:
一般地,如果a,b表示整式,且b中含有字母,式子 叫做分式 ,
其中,a叫做分式的分子,b叫做分式的分母且b≠0.
(2)分式的基本性质:
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
表达式: (c≠0),其中a,b,c是整式.
三、知识梳理
(3)通分与约分
把一个分式的分子与分母的公因式约去,叫做分式的约分.
分子与分母只有公因式1的式子,叫做最简分式.
使分子、分母同乘适当的整式,把分母不相同的分式变成分母相同的分式,
这种变形叫分式的通分.
一般取各分母的所有因式的最高次幂的积作公分母,叫做最简公分母.
典型例题
分析:根据分式值为0的条件:分子为0而分母不为0,列出关于x的方程,求
出x的值,并检验当x的取值时分式的分母的对应值是否为零.由题意可得:
x2-1=0, 解得x=±1.当x=-1时,x+1=0;当x=1时,x+1 ≠0.
例1.如果分式 的值为0,那么x的值为 .
1
归纳拓展:分式有意义的条件是分母不为0;分式无意义的条件是分母的
值为0;分式的值为0的条件是:分子为0而分母不为0.
2
C
x=-1或 x=2
1.如果分式 的值为零,则a的值为 .
2.若代数式 在实数范围内有意义,则实数x的取值范围是 ( )
A.x<3 B.x>3 C.x≠3 D.x=3
3.若分式 没有意义,则x应满足的条件是: .
【当堂检测】
典型例题
例2.下列约分正确的是( )
D
A.
B.
C.
D.
解析:A项和C项不能约分,B项约分结果是1,只有D项约分正确;故选D.
【当堂检测】
4.先约分,再求值: ,其中a=1,b=2.
把a=1,b=2代入,
=-2.
原式
解:
三、知识梳理
2.分式的运算
(1)分式的乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
(2)分式的除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示为:
用式子表示为:
三、知识梳理
(3)分式的乘方法则:
分式乘方要把分子、分母分别乘方.
用式子表示为:
(4)分式的加减法则:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
± =
± = ± =
典型例题
分析:本题中给出字母的具体取值,因此要先化简分式再代入求值.
例3.已知分式x=4 ,y=2 , 求 的值.
解:原式=
把x=4,y=2代入得:
原式=
典型例题
归纳总结:对于一个分式,如果给出其中字母的取值,我们可以先将分式
进行化简,再把字母取值代入,即可求出分式的值.但对于某些分式的求值
问题,却没有直接给出字母的取值,而只是给出字母满足的条件,这样的问
题较复杂,需要根据具体情况选择适当的方法.
【当堂检测】
x-2y
5.化简:(1) 的结果是 ;
(2) 的结果是 .
1
【当堂检测】
6.已知 ,求出 的值.
解:
原式=(32-2)2-2=47.
当 =3,
【当堂检测】
7.先化简,再求值: ,其中m2+3m=-1.
解:原式=
因为m2+3m=-1,
所以3m2+9m=-3,
所以原式= .
三、知识梳理
3.分式方程
(1)分式方程的概念:
(2)解分式方程:
(3)分式方程的检验:
分母中含未知数的方程叫做分式方程.
分式方程
整式方程
去分母
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式
方程的解是原分式方程的解;否则,这个解就是增根.
典型例题
例4.解方程:
解:(1)方程两边同时乘x2-4得:
2(x+2)-8=0.
检验:当x=2时,x2-4=0,因此x=2不是原分式方程的解.
∴原分式方程无解.
解得:
x=2.
典型例题
例4.解方程:
解:(1)方程两边同时乘2x+2得:
6x=3x+2x+2.
检验:当x=2时,2x+2≠0.
所以原分式方程的解为x=2.
解得:
x=2.
典型例题
例5.某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨
9000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果
数量比第一次的2倍还多300 kg.该干果第一次的进价是多少?
解:设该种干果第一次的进价是x元/kg,则第二次的进价是(1+20%)x元/kg.
经检验,x=5是原分式方程的解,且符合题意.
答:该种干果第一次的进价是5元/kg.
解得x=5.
由题意,得
典型例题
归纳总结:解分式方程,要注意基本步骤,即一化二解三检验.要特别注意
一化时乘以最简公分母.另外要特别注意检验.
列分式方程解应用题的基本步骤是:(1)审(2)找(3)设(4)列(5)解(6)验(7)答.
列分式方程解应用题要特别注意找相等关系,这是列方程最关键的步骤.
【当堂检测】
8.解方程:
解:方程两边同时乘x(x-2)得:
(x-2)(2x+2)-x(x+2)=x2-2
解得:
经检验, 是原分式方程的解.
【当堂检测】
9.某市为进一步缓解交通拥堵现象,决定修建一条从市中心到机场的轻轨
铁路.实际施工时,每月的工效比原计划提高了20%,结果提前5个月完成
这一工程.求原计划完成这一工程的时间是多少个月.
解:设原计划完成这一工程的时间为x个月.
经检验,x=30是原分式方程的解,且符合题意.
答:原计划完成这一工程的时间是30个月.
解得x=30.
由题意,得
四、课堂总结
分式
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
步骤
一审二找三设四列五解六检
七写,尤其不要忘了验证
类型
行程、工程、销售问题等
分式的运算及化简求值
分式方程的定义
分式方程的解法及验证
第 9 章 分式
复习课
一、学习目标
1.巩固分式的相关概念及其基本性质;
2.能熟练地进行分式的相关运算,解分式方程;
3.能用分式方程解决相关数学问题与生活中的实际问题.
二、知识结构
分式
分式的定义
分式的基本性质
约分
通分
分式的运算
分式的乘方
分式的乘除
分式的加减
分式的
混合运算
分式的
化简求值
分式方程的概念
分式方程的解法
分式方程的应用
三、知识梳理
1.分式的概念与基本性质
(1)分式的概念:
一般地,如果a,b表示整式,且b中含有字母,式子 叫做分式 ,
其中,a叫做分式的分子,b叫做分式的分母且b≠0.
(2)分式的基本性质:
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
表达式: (c≠0),其中a,b,c是整式.
三、知识梳理
(3)通分与约分
把一个分式的分子与分母的公因式约去,叫做分式的约分.
分子与分母只有公因式1的式子,叫做最简分式.
使分子、分母同乘适当的整式,把分母不相同的分式变成分母相同的分式,
这种变形叫分式的通分.
一般取各分母的所有因式的最高次幂的积作公分母,叫做最简公分母.
典型例题
分析:根据分式值为0的条件:分子为0而分母不为0,列出关于x的方程,求
出x的值,并检验当x的取值时分式的分母的对应值是否为零.由题意可得:
x2-1=0, 解得x=±1.当x=-1时,x+1=0;当x=1时,x+1 ≠0.
例1.如果分式 的值为0,那么x的值为 .
1
归纳拓展:分式有意义的条件是分母不为0;分式无意义的条件是分母的
值为0;分式的值为0的条件是:分子为0而分母不为0.
2
C
x=-1或 x=2
1.如果分式 的值为零,则a的值为 .
2.若代数式 在实数范围内有意义,则实数x的取值范围是 ( )
A.x<3 B.x>3 C.x≠3 D.x=3
3.若分式 没有意义,则x应满足的条件是: .
【当堂检测】
典型例题
例2.下列约分正确的是( )
D
A.
B.
C.
D.
解析:A项和C项不能约分,B项约分结果是1,只有D项约分正确;故选D.
【当堂检测】
4.先约分,再求值: ,其中a=1,b=2.
把a=1,b=2代入,
=-2.
原式
解:
三、知识梳理
2.分式的运算
(1)分式的乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.
(2)分式的除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
用式子表示为:
用式子表示为:
三、知识梳理
(3)分式的乘方法则:
分式乘方要把分子、分母分别乘方.
用式子表示为:
(4)分式的加减法则:
同分母分式相加减,分母不变,把分子相加减;
异分母分式相加减,先通分,变为同分母的分式,再加减.
± =
± = ± =
典型例题
分析:本题中给出字母的具体取值,因此要先化简分式再代入求值.
例3.已知分式x=4 ,y=2 , 求 的值.
解:原式=
把x=4,y=2代入得:
原式=
典型例题
归纳总结:对于一个分式,如果给出其中字母的取值,我们可以先将分式
进行化简,再把字母取值代入,即可求出分式的值.但对于某些分式的求值
问题,却没有直接给出字母的取值,而只是给出字母满足的条件,这样的问
题较复杂,需要根据具体情况选择适当的方法.
【当堂检测】
x-2y
5.化简:(1) 的结果是 ;
(2) 的结果是 .
1
【当堂检测】
6.已知 ,求出 的值.
解:
原式=(32-2)2-2=47.
当 =3,
【当堂检测】
7.先化简,再求值: ,其中m2+3m=-1.
解:原式=
因为m2+3m=-1,
所以3m2+9m=-3,
所以原式= .
三、知识梳理
3.分式方程
(1)分式方程的概念:
(2)解分式方程:
(3)分式方程的检验:
分母中含未知数的方程叫做分式方程.
分式方程
整式方程
去分母
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式
方程的解是原分式方程的解;否则,这个解就是增根.
典型例题
例4.解方程:
解:(1)方程两边同时乘x2-4得:
2(x+2)-8=0.
检验:当x=2时,x2-4=0,因此x=2不是原分式方程的解.
∴原分式方程无解.
解得:
x=2.
典型例题
例4.解方程:
解:(1)方程两边同时乘2x+2得:
6x=3x+2x+2.
检验:当x=2时,2x+2≠0.
所以原分式方程的解为x=2.
解得:
x=2.
典型例题
例5.某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨
9000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果
数量比第一次的2倍还多300 kg.该干果第一次的进价是多少?
解:设该种干果第一次的进价是x元/kg,则第二次的进价是(1+20%)x元/kg.
经检验,x=5是原分式方程的解,且符合题意.
答:该种干果第一次的进价是5元/kg.
解得x=5.
由题意,得
典型例题
归纳总结:解分式方程,要注意基本步骤,即一化二解三检验.要特别注意
一化时乘以最简公分母.另外要特别注意检验.
列分式方程解应用题的基本步骤是:(1)审(2)找(3)设(4)列(5)解(6)验(7)答.
列分式方程解应用题要特别注意找相等关系,这是列方程最关键的步骤.
【当堂检测】
8.解方程:
解:方程两边同时乘x(x-2)得:
(x-2)(2x+2)-x(x+2)=x2-2
解得:
经检验, 是原分式方程的解.
【当堂检测】
9.某市为进一步缓解交通拥堵现象,决定修建一条从市中心到机场的轻轨
铁路.实际施工时,每月的工效比原计划提高了20%,结果提前5个月完成
这一工程.求原计划完成这一工程的时间是多少个月.
解:设原计划完成这一工程的时间为x个月.
经检验,x=30是原分式方程的解,且符合题意.
答:原计划完成这一工程的时间是30个月.
解得x=30.
由题意,得
四、课堂总结
分式
分式
分式的定义及有意义的条件等
分式方程
分式方程的应用
步骤
一审二找三设四列五解六检
七写,尤其不要忘了验证
类型
行程、工程、销售问题等
分式的运算及化简求值
分式方程的定义
分式方程的解法及验证
