2023-2024学年初中数学沪科版七年级下册第10章相交线、平行线和平移复习课课件(共29张PPT)
文档属性
| 名称 | 2023-2024学年初中数学沪科版七年级下册第10章相交线、平行线和平移复习课课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:24:22 | ||
图片预览








文档简介
(共29张PPT)
第 10 章 相交线、平行线与平移
复习课
一、学习目标
1.掌握对顶角、垂线的概念和性质;
2.理解同位角、内错角、同旁内角的概念;
3.掌握平行线的概念、性质,会判断两条直线是否平行,能综合运用
平行线的性质和判定解决问题;
4.知道平移的概念、性质.
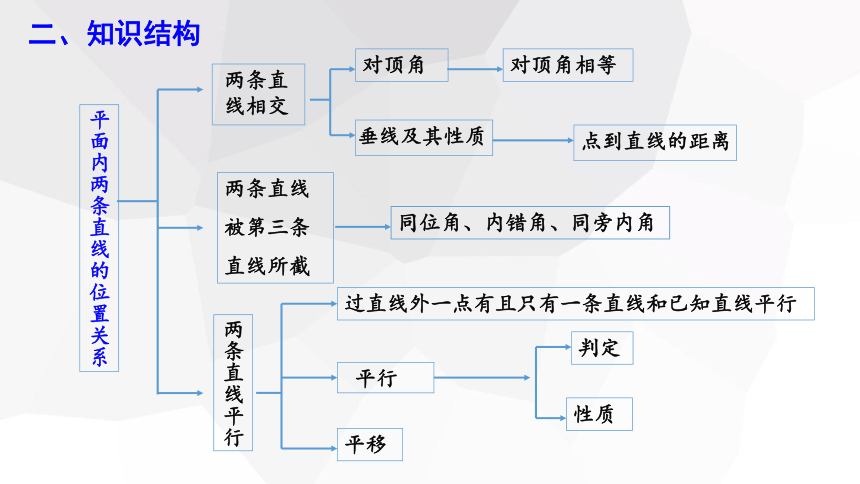
二、知识结构
对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条直线相交
两条直线
被第三条
直线所截
平面内两条直线的位置关系
同位角、内错角、同旁内角
两条直线平行
平行
平移
判定
性质
过直线外一点有且只有一条直线和已知直线平行
三、知识回顾
(1)两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.如图
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.
2.对顶角性质:对顶角相等.
两个特征:(1) 具有公共顶点;(2) 角的两边互为反向延长线.
∠1和∠2, ∠3和∠4是对顶角.
1. 对顶角:
知识点一 对顶角
1. 垂线的性质:
知识点二 垂线
(2)直线外一点与直线上各点连结的所有线段中,垂线段最短.
简称:垂线段最短.
2.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、知识回顾
(1)过一点有且只有一条直线与已知直线垂直.
典型例题
例1.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
因为AB⊥CD,(已知)
因为∠AOE=65°,(已知)
所以∠AOC=90°.(垂直的定义)
所以∠COE=25°(两角差的性质)
又因为∠COE=∠DOF (对顶角相等)
所以∠DOF=25°.(等量代换)
典型例题
例2.如图,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由;
(2)从码头到铁路怎样走最近?画图并说明理由;
(3)从火车站到河流怎样走最近?画图并说明理由.
分析:(1)从火车站到码头的距离是点到点的距离,即两点间的距离.
依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
典型例题
(3)沿AC走最近,理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
解:如图所示:
(1)沿AB走最近,理由:两点之间的所有连线中,线段最短.
(2)沿BD走最近,理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
归纳总结:(1)两条直线相交形成2对对顶角;对顶角相等.
(2)垂直是相交的一种特殊情况,当两条直线相交,夹角等于90°时,这两
条直线就互相垂直了.我们往往利用“直线外一点与直线上各点连接的所有
线段中,垂线段最短”来解决实际问题,这时要应用转化思想将实际问题转
化为“点到线的距离”问题来解决.
典型例题
【当堂检测】
1.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF的度数.
解:因为AB⊥OE (已知)
因为∠DOE= 50°,(已知)
所以 ∠EOB=90°,(垂直的定义)
所以∠DOB=40°,(余角的定义)
所以∠AOC=∠DOB=40°,(对顶角相等)
又因为OB平分∠DOF,(已知)
所以∠BOF= ∠DOB=40°.(角平分线性质)
所以∠EOF= ∠EOB+ ∠BOF=90°+40°=130°.(两角和的定义)
【当堂检测】
2.如图,直线l表示一条公路,点P是火车站所在的位置,要修一条从火车站
到公路的道路,有如下3种方式,选择哪种方式才能使道路最短?
理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
选择方式2才能使道路最短.
l
P
方
式
1
方
式
2
方
式
3
【当堂检测】
3.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.
4.8
6
8
知识点三 平行线
1.平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
2. 平行线的基本性质:
(2) 两条平行线之间的距离处处相等.
(1)经过直线外一点,有且只有一条直线与已知直线平行.
三、知识回顾
知识点四 同位角、内错角、同旁内角
同位角的位置特征是: (1)在截线的同旁,(2)被截两直线的同方向.
内错角的位置特征是: (1)在截线的两旁,(2)在被截两直线之间.
同旁内角的位置特征是: (1)在截线的同旁,(2)在被截两直线之间.
三、知识回顾
知识点五 平行线的判定
1.三种角判定(3种方法):
2.在同一平面内,垂直于同一条直线的两条直线平行.
(3)同旁内角互补,两直线平行.
(2)内错角相等,两直线平行;
(1)同位角相等,两直线平行;
三、知识回顾
知识点六 平行线的性质
(1)两直线平行,同位角相等;
(3)两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;
(4)平行于同一条直线的两条直线平行.
三、知识回顾
例2.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2的相等吗?说明理由.
解:∠1与∠2 的度数相等.
理由:∵直线a、b 被c 、d所截,且 c⊥a, c⊥b,
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
a
b
c
d
典型例题
归纳总结:综合题目中可先由角的数量关系判定两直线互相平行,再根据平
行线的性质得出另一对角相等或互补,从而进行相关的计算或说理;或先通
过平行线得出两个角的关系,再根据平行线的判定得出另一组直线互相平行.
典型例题
【当堂检测】
A
B
C
D
E
F
1
2
3
4.填空:
(1)∵∠A=____, (已知)
AC∥ED ,( )
(2) ∵AB ∥______, (已知)
∠2= ∠4,( )
4
5
(3) ___ ∥___, (已知)
∠B= ∠3. ( )
∠4
同位角相等,两直线平行.
DF
两直线平行, 内错角相等.
AB
DF
两直线平行, 同位角相等.
∴
∴
∴
∵
【当堂检测】
5.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,
求∠FEC的度数.
因为EF∥BC,所以∠FEC=∠ECB,所以∠FEC=20°.
解:因为EF∥AD,AD∥BC,所以EF∥BC,
因为∠DAC=120°,所以∠ACB=60°.
又因为∠ACF=20°,所以∠FCB=∠ACB-∠ACF=40°.
因为CE平分∠BCF,所以∠BCE=20°.
所以∠ACB+∠DAC=180°.
知识点七 平移
1.平移的概念
(1)平移的两个图形形状和大小完全相同
(2)对应线段平行(或在同一直线上)且相等,对应角相等;
(3)各对应点所连线段平行(或在同一直线上)且相等;
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动称为平移.
2.平移的性质
三、知识回顾
例3.如图,将图形中的三角形ABC向左平移4格,然后再向下平移2格,
画出平移后的图形.
典型例题
分析:本题可分两步来作图.先作三角形ABC
向左平移4格的图形,再将该图向下平移2格,
即为所求.
找到关键点A,B,C,先将点A,B,C分别向左平移4格到点A1,B1,C1,
顺次连接各点,三角形A1B1C1即为三角形ABC向左平移4格后得到的图形.
再用同样的方法,将点A1,B1,C1向下平移2格,得对应点A′,B′,C′,
连接得三角形A′B′C′,即为所求图形.
典型例题
解:如图△A′B′C′即为所求.
归纳总结:在平面内,一个图形平移后得到的图形与原图形的对应线段相等,
对应角相等,各对应点所连接的线段平行(或在同一条直线上)且相等.
在利用平移的性质作图时,把每一个关键点按要求的方向和距离平移,
再把所得的对应点顺次连接即可.
典型例题
例4.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着
点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,
求阴影部分的面积.
解:
因为两个三角形大小一样,
所以阴影部分的面积等于梯形ABEH的面积.
由平移的性质,得DE=AB,BE=6.
因为AB=10,DH=4,
所以HE=DE-DH=10-4=6,
所以阴影部分的面积= ×(6+10)×6=48.
典型例题
归纳总结:图形平行的性质:
(1)图形平移前后的对应的线段相等,对应角相等.
(2)图形平移前后的对应线段共线或平行.
(3)图形平移前后的对应点的连线共线或平行.
6.如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
D
【当堂检测】
【当堂检测】
7.如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是( )
A.∠F;AC
B.∠BOD;BA
C.∠F;BA
D.∠BOD;AC
C
【当堂检测】
8.如图,△ABC沿直线l向右移了3 cm,得到△FDE,且BC=6 cm,∠ABC=45°.
(1)求BE的长;(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
解:
(1)因为△ABC沿着直线l向右移了3 cm,
所以CE=BD=3 cm,所以BE=BC+CE=6+3=9 (cm).
(4)互相平行的线段:AB∥FD,AC∥FE.
(3)相等的线段:AB=FD,AC=FE,BC=DE,BD=DC=CE.
(2)根据平移的性质可得∠FDE=∠ABC=45°,
所以∠FDB=180°-45°=135°.
四、课堂总结
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线平行
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
平移
第 10 章 相交线、平行线与平移
复习课
一、学习目标
1.掌握对顶角、垂线的概念和性质;
2.理解同位角、内错角、同旁内角的概念;
3.掌握平行线的概念、性质,会判断两条直线是否平行,能综合运用
平行线的性质和判定解决问题;
4.知道平移的概念、性质.
二、知识结构
对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条直线相交
两条直线
被第三条
直线所截
平面内两条直线的位置关系
同位角、内错角、同旁内角
两条直线平行
平行
平移
判定
性质
过直线外一点有且只有一条直线和已知直线平行
三、知识回顾
(1)两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角.如图
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角.
2.对顶角性质:对顶角相等.
两个特征:(1) 具有公共顶点;(2) 角的两边互为反向延长线.
∠1和∠2, ∠3和∠4是对顶角.
1. 对顶角:
知识点一 对顶角
1. 垂线的性质:
知识点二 垂线
(2)直线外一点与直线上各点连结的所有线段中,垂线段最短.
简称:垂线段最短.
2.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
三、知识回顾
(1)过一点有且只有一条直线与已知直线垂直.
典型例题
例1.如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
因为AB⊥CD,(已知)
因为∠AOE=65°,(已知)
所以∠AOC=90°.(垂直的定义)
所以∠COE=25°(两角差的性质)
又因为∠COE=∠DOF (对顶角相等)
所以∠DOF=25°.(等量代换)
典型例题
例2.如图,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由;
(2)从码头到铁路怎样走最近?画图并说明理由;
(3)从火车站到河流怎样走最近?画图并说明理由.
分析:(1)从火车站到码头的距离是点到点的距离,即两点间的距离.
依据两点之间线段最短解答.
(2)从码头到铁路的距离是点到直线的距离.依据垂线段最短解答.
(3)从火车站到河流的距离是点到直线的距离.依据垂线段最短解答.
典型例题
(3)沿AC走最近,理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
解:如图所示:
(1)沿AB走最近,理由:两点之间的所有连线中,线段最短.
(2)沿BD走最近,理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
归纳总结:(1)两条直线相交形成2对对顶角;对顶角相等.
(2)垂直是相交的一种特殊情况,当两条直线相交,夹角等于90°时,这两
条直线就互相垂直了.我们往往利用“直线外一点与直线上各点连接的所有
线段中,垂线段最短”来解决实际问题,这时要应用转化思想将实际问题转
化为“点到线的距离”问题来解决.
典型例题
【当堂检测】
1.如图.直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF的度数.
解:因为AB⊥OE (已知)
因为∠DOE= 50°,(已知)
所以 ∠EOB=90°,(垂直的定义)
所以∠DOB=40°,(余角的定义)
所以∠AOC=∠DOB=40°,(对顶角相等)
又因为OB平分∠DOF,(已知)
所以∠BOF= ∠DOB=40°.(角平分线性质)
所以∠EOF= ∠EOB+ ∠BOF=90°+40°=130°.(两角和的定义)
【当堂检测】
2.如图,直线l表示一条公路,点P是火车站所在的位置,要修一条从火车站
到公路的道路,有如下3种方式,选择哪种方式才能使道路最短?
理由:直线外一点与直线上各点连接的所有线段中,
垂线段最短.
选择方式2才能使道路最短.
l
P
方
式
1
方
式
2
方
式
3
【当堂检测】
3.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.
4.8
6
8
知识点三 平行线
1.平行线的概念:
在同一平面内,不相交的两条直线叫做平行线.
2. 平行线的基本性质:
(2) 两条平行线之间的距离处处相等.
(1)经过直线外一点,有且只有一条直线与已知直线平行.
三、知识回顾
知识点四 同位角、内错角、同旁内角
同位角的位置特征是: (1)在截线的同旁,(2)被截两直线的同方向.
内错角的位置特征是: (1)在截线的两旁,(2)在被截两直线之间.
同旁内角的位置特征是: (1)在截线的同旁,(2)在被截两直线之间.
三、知识回顾
知识点五 平行线的判定
1.三种角判定(3种方法):
2.在同一平面内,垂直于同一条直线的两条直线平行.
(3)同旁内角互补,两直线平行.
(2)内错角相等,两直线平行;
(1)同位角相等,两直线平行;
三、知识回顾
知识点六 平行线的性质
(1)两直线平行,同位角相等;
(3)两直线平行,同旁内角互补;
(2)两直线平行,内错角相等;
(4)平行于同一条直线的两条直线平行.
三、知识回顾
例2.如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2的相等吗?说明理由.
解:∠1与∠2 的度数相等.
理由:∵直线a、b 被c 、d所截,且 c⊥a, c⊥b,
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
a
b
c
d
典型例题
归纳总结:综合题目中可先由角的数量关系判定两直线互相平行,再根据平
行线的性质得出另一对角相等或互补,从而进行相关的计算或说理;或先通
过平行线得出两个角的关系,再根据平行线的判定得出另一组直线互相平行.
典型例题
【当堂检测】
A
B
C
D
E
F
1
2
3
4.填空:
(1)∵∠A=____, (已知)
AC∥ED ,( )
(2) ∵AB ∥______, (已知)
∠2= ∠4,( )
4
5
(3) ___ ∥___, (已知)
∠B= ∠3. ( )
∠4
同位角相等,两直线平行.
DF
两直线平行, 内错角相等.
AB
DF
两直线平行, 同位角相等.
∴
∴
∴
∵
【当堂检测】
5.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,
求∠FEC的度数.
因为EF∥BC,所以∠FEC=∠ECB,所以∠FEC=20°.
解:因为EF∥AD,AD∥BC,所以EF∥BC,
因为∠DAC=120°,所以∠ACB=60°.
又因为∠ACF=20°,所以∠FCB=∠ACB-∠ACF=40°.
因为CE平分∠BCF,所以∠BCE=20°.
所以∠ACB+∠DAC=180°.
知识点七 平移
1.平移的概念
(1)平移的两个图形形状和大小完全相同
(2)对应线段平行(或在同一直线上)且相等,对应角相等;
(3)各对应点所连线段平行(或在同一直线上)且相等;
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动称为平移.
2.平移的性质
三、知识回顾
例3.如图,将图形中的三角形ABC向左平移4格,然后再向下平移2格,
画出平移后的图形.
典型例题
分析:本题可分两步来作图.先作三角形ABC
向左平移4格的图形,再将该图向下平移2格,
即为所求.
找到关键点A,B,C,先将点A,B,C分别向左平移4格到点A1,B1,C1,
顺次连接各点,三角形A1B1C1即为三角形ABC向左平移4格后得到的图形.
再用同样的方法,将点A1,B1,C1向下平移2格,得对应点A′,B′,C′,
连接得三角形A′B′C′,即为所求图形.
典型例题
解:如图△A′B′C′即为所求.
归纳总结:在平面内,一个图形平移后得到的图形与原图形的对应线段相等,
对应角相等,各对应点所连接的线段平行(或在同一条直线上)且相等.
在利用平移的性质作图时,把每一个关键点按要求的方向和距离平移,
再把所得的对应点顺次连接即可.
典型例题
例4.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着
点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,
求阴影部分的面积.
解:
因为两个三角形大小一样,
所以阴影部分的面积等于梯形ABEH的面积.
由平移的性质,得DE=AB,BE=6.
因为AB=10,DH=4,
所以HE=DE-DH=10-4=6,
所以阴影部分的面积= ×(6+10)×6=48.
典型例题
归纳总结:图形平行的性质:
(1)图形平移前后的对应的线段相等,对应角相等.
(2)图形平移前后的对应线段共线或平行.
(3)图形平移前后的对应点的连线共线或平行.
6.如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
D
【当堂检测】
【当堂检测】
7.如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是( )
A.∠F;AC
B.∠BOD;BA
C.∠F;BA
D.∠BOD;AC
C
【当堂检测】
8.如图,△ABC沿直线l向右移了3 cm,得到△FDE,且BC=6 cm,∠ABC=45°.
(1)求BE的长;(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
解:
(1)因为△ABC沿着直线l向右移了3 cm,
所以CE=BD=3 cm,所以BE=BC+CE=6+3=9 (cm).
(4)互相平行的线段:AB∥FD,AC∥FE.
(3)相等的线段:AB=FD,AC=FE,BC=DE,BD=DC=CE.
(2)根据平移的性质可得∠FDE=∠ABC=45°,
所以∠FDB=180°-45°=135°.
四、课堂总结
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线平行
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
平移
