2023-2024学年初中数学北师大版八年级下册2.1 不等关系课件(共13张PPT)
文档属性
| 名称 | 2023-2024学年初中数学北师大版八年级下册2.1 不等关系课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 153.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第二章 一元一次不等式
与一元一次不等式组
2.1 不等关系
1.了解不等式的定义
2.会列不等式表示简单的不等关系
一、学习目标
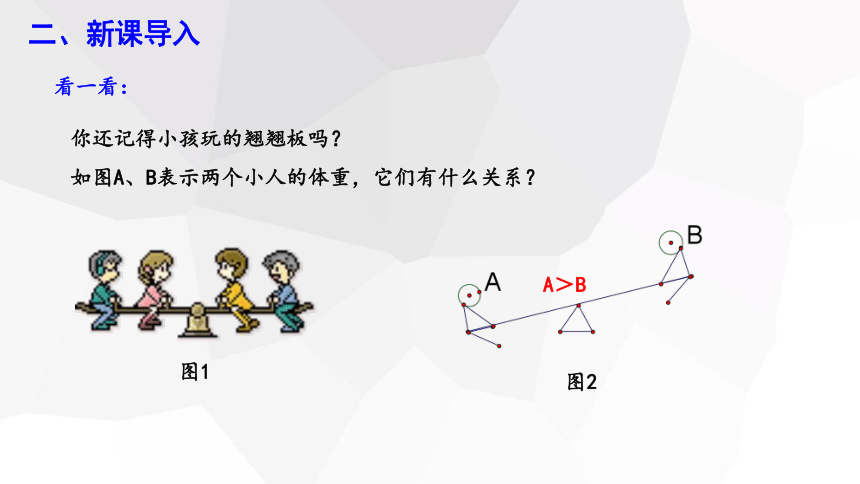
二、新课导入
看一看:
你还记得小孩玩的翘翘板吗?
如图A、B表示两个小人的体重,它们有什么关系?
图1
图2
A>B
(一)不等关系
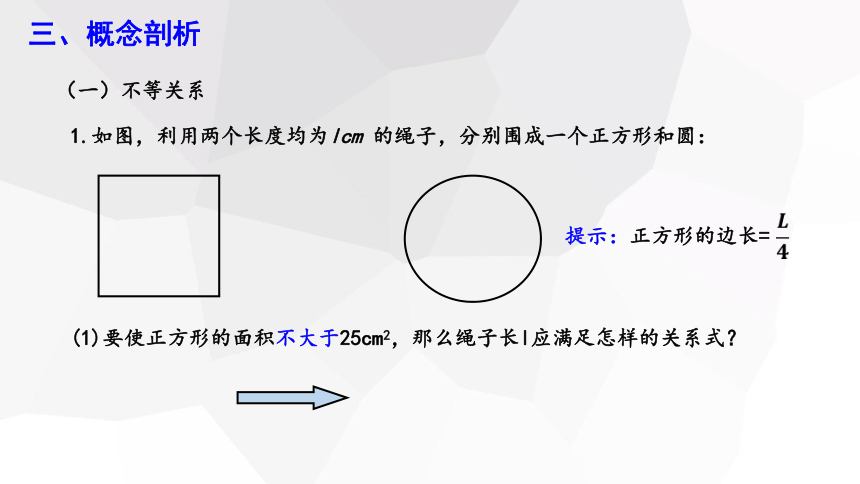
三、概念剖析
(1)要使正方形的面积不大于25cm2,那么绳子长l应满足怎样的关系式?
1.如图,利用两个长度均为lcm 的绳子,分别围成一个正方形和圆:
提示:正方形的边长=
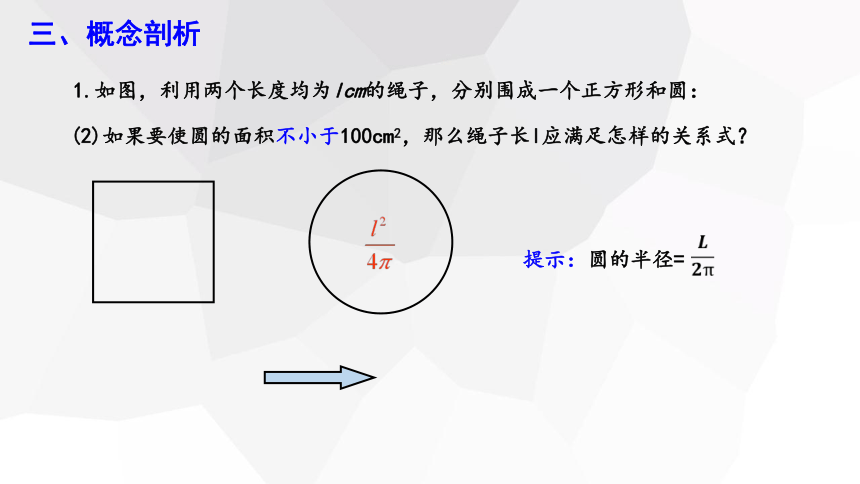
三、概念剖析
(2)如果要使圆的面积不小于100cm2,那么绳子长l应满足怎样的关系式?
1.如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
提示:圆的半径=
三、概念剖析
像上面的“不大于”、“不小于”都是用来描述不等关系的词语
我们得到的式子:
① A>B
②
都含不等号
它们有什么特点?
像上面这样用“<”(或“≤”),“>”(或“≥”)连接的
式子叫做不等式.
(二)不等式的定义
三、概念剖析
火眼金睛:
下列式子哪些是不等式?
①-1≠0;
②x<1;
③s=vt;
④a2+b2≥0;
⑤y≤4;
⑥x2-2x+3.
√
注意:“≠”也是不等号.
√
√
√
等式
代数式
1.不等关系
归纳:
三、概念剖析
(1)列不等式的关键是用不等号准确表示描述不等关系的词语.
(2)常见的描述不等关系的词语有“大于”“小于”“至少”“最多”
“不大于”“不小于”“超过”“不足”等.
2.不等式的定义
一般地,用“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式
四、典型例题
例1:用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过学生年龄的2倍。
解:
(4)设老师的年龄为x,学生的年龄为y,
则x≤2y
(3)设海洋的面积为S海,陆地面积为S陆,
(1)3x+8<5x
(2)x2≥0
则S海>S陆
【当堂检测】
1.铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160㎝,设行李的长、宽、高分别为a ㎝、b ㎝、c ㎝,则行李的长、宽、高满足的关系式为( )
A.a+b+c>160 B.a+b+c<60
C.a+b+c≥60 D.a+b+c≤160
D
2.用适当的符号表示下列关系:
(1) a是负数; (2) a是非负数;
(3) a与b的和小于5; (4) x与2的差大于-1;
(5) x的4倍不大于7; (6) y的一半不小于3.
4x≤7
y≥3
a<0
a≥0
a+b<5
x-2>-1
四、典型例题
例2: 下列各式中的不等式有哪些?
(1)8<9; (2)a+b=0;
(3)a2+1>0; (4)3x-1≤x;
(5)x-y≠1; (6)3-x=0;
(7)4-2x; (8)x2+y2>0.
√
√
√
√
√
代数式
二元一次方程
一元一次方程
提示:结合不等式的定义进行判断
【当堂检测】
3.下列说法不正确的是( )
A.4<5是不等式
B.x2+1≠0是不等式
C.3a2+a=0是不等式
D.a2+2a≥4a-2是不等式
4.边长为a的正方形的周长不大于直径为2b的圆的面积的不等关系为:
.
4a≤πb2
C
1.不等式的定义
五、课堂总结
一般地,用“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式
注意:“≠”也是不等号.
2.列不等式
用不等号准确表示描述不等关系的词语,再列出不等式.
第二章 一元一次不等式
与一元一次不等式组
2.1 不等关系
1.了解不等式的定义
2.会列不等式表示简单的不等关系
一、学习目标
二、新课导入
看一看:
你还记得小孩玩的翘翘板吗?
如图A、B表示两个小人的体重,它们有什么关系?
图1
图2
A>B
(一)不等关系
三、概念剖析
(1)要使正方形的面积不大于25cm2,那么绳子长l应满足怎样的关系式?
1.如图,利用两个长度均为lcm 的绳子,分别围成一个正方形和圆:
提示:正方形的边长=
三、概念剖析
(2)如果要使圆的面积不小于100cm2,那么绳子长l应满足怎样的关系式?
1.如图,利用两个长度均为lcm的绳子,分别围成一个正方形和圆:
提示:圆的半径=
三、概念剖析
像上面的“不大于”、“不小于”都是用来描述不等关系的词语
我们得到的式子:
① A>B
②
都含不等号
它们有什么特点?
像上面这样用“<”(或“≤”),“>”(或“≥”)连接的
式子叫做不等式.
(二)不等式的定义
三、概念剖析
火眼金睛:
下列式子哪些是不等式?
①-1≠0;
②x<1;
③s=vt;
④a2+b2≥0;
⑤y≤4;
⑥x2-2x+3.
√
注意:“≠”也是不等号.
√
√
√
等式
代数式
1.不等关系
归纳:
三、概念剖析
(1)列不等式的关键是用不等号准确表示描述不等关系的词语.
(2)常见的描述不等关系的词语有“大于”“小于”“至少”“最多”
“不大于”“不小于”“超过”“不足”等.
2.不等式的定义
一般地,用“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式
四、典型例题
例1:用适当的符号表示下列关系:
(1)x的3倍与8的和比x的5倍小;
(2)x2是非负数;
(3)地球上海洋的面积大于陆地面积;
(4)老师的年龄不超过学生年龄的2倍。
解:
(4)设老师的年龄为x,学生的年龄为y,
则x≤2y
(3)设海洋的面积为S海,陆地面积为S陆,
(1)3x+8<5x
(2)x2≥0
则S海>S陆
【当堂检测】
1.铁路部门对旅客随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160㎝,设行李的长、宽、高分别为a ㎝、b ㎝、c ㎝,则行李的长、宽、高满足的关系式为( )
A.a+b+c>160 B.a+b+c<60
C.a+b+c≥60 D.a+b+c≤160
D
2.用适当的符号表示下列关系:
(1) a是负数; (2) a是非负数;
(3) a与b的和小于5; (4) x与2的差大于-1;
(5) x的4倍不大于7; (6) y的一半不小于3.
4x≤7
y≥3
a<0
a≥0
a+b<5
x-2>-1
四、典型例题
例2: 下列各式中的不等式有哪些?
(1)8<9; (2)a+b=0;
(3)a2+1>0; (4)3x-1≤x;
(5)x-y≠1; (6)3-x=0;
(7)4-2x; (8)x2+y2>0.
√
√
√
√
√
代数式
二元一次方程
一元一次方程
提示:结合不等式的定义进行判断
【当堂检测】
3.下列说法不正确的是( )
A.4<5是不等式
B.x2+1≠0是不等式
C.3a2+a=0是不等式
D.a2+2a≥4a-2是不等式
4.边长为a的正方形的周长不大于直径为2b的圆的面积的不等关系为:
.
4a≤πb2
C
1.不等式的定义
五、课堂总结
一般地,用“<”(或“≤”),“>”(或“≥”) 连接的式子叫做不等式
注意:“≠”也是不等号.
2.列不等式
用不等号准确表示描述不等关系的词语,再列出不等式.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
