2.5 一元一次不等式与一次函数 第2课时 课件(共18张PPT) 2023-2024学年初中数学北师大版八年级下册
文档属性
| 名称 | 2.5 一元一次不等式与一次函数 第2课时 课件(共18张PPT) 2023-2024学年初中数学北师大版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:21:15 | ||
图片预览






文档简介
(共18张PPT)
第二章 一元一次不等式
与一元一次不等式组
2.5 一元一次不等式与一次函数
第2课时
1.能用一次函数和一元一次不等式解决实际问题 (重点)
2.体会不等式、函数、方程的内在联系
一、学习目标
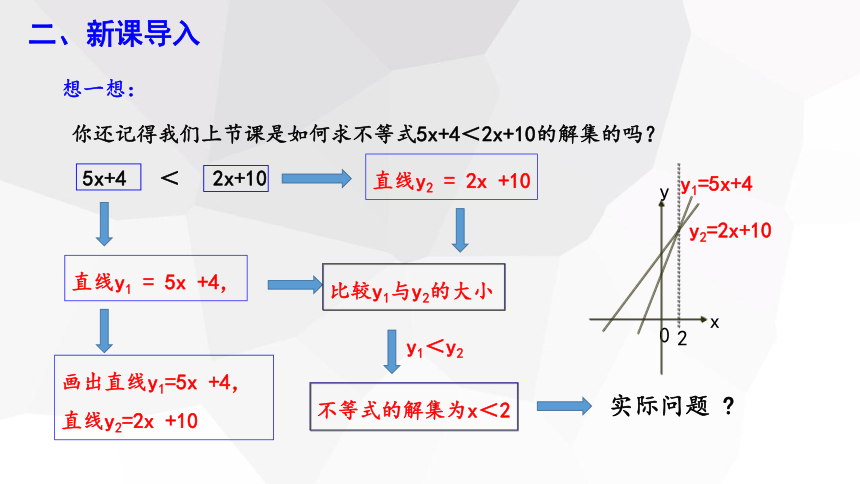
二、新课导入
想一想:
你还记得我们上节课是如何求不等式5x+4<2x+10的解集的吗?
画出直线y1=5x +4,
直线y2=2x +10
x
y
0
2
y2=2x+10
y1=5x+4
不等式的解集为x<2
5x+4 < 2x+10
直线y1 = 5x +4,
直线y2 = 2x +10
比较y1与y2的大小
实际问题
y1<y2
三、典型例题
例1.某商店5月1日举行促销活动,当天到该商店购买商品有两种优惠方案:
方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,
一律按商品价格的8折优惠;
方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5
折优惠.
目标 会利用一次函数和一元一次不等式选择最优方案
三、典型例题
已知小敏5月1日前不是该商店的会员.
(1)若小敏不购买会员卡,当所购买商品的价格为120元时,
实际应支付多少元?
所以实际应支付114元.
解:(1)120×0.95=114(元),
方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,
一律按商品价格的8折优惠;
方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.
三、典型例题
(2)请帮小敏算一算:所购买商品的价格在什么范围内时,采用方案一更合算?
所购买商品的价格在什么范围内时,采用方案二更合算?
(2)设购买商品的价格为x元,
则采用方案一实际应支付(0.8x+168)元,
当0.8x+168<0.95x时,解得x>1120;
当0.8x+168>0.95x时,解得x<1120.
故当购买商品的价格超过1120元时,采用方案一更合算;
当购买商品的价格小于1120元时,采用方案二更合算.
采用方案二实际应支付0.95x元.
三、典型例题
归纳总结:
结合“新课导入”中求不等式5x+4<2x+10的解集,我们知道可以通过比较函数值的大小,求解集.
那么在实际问题中,我们可以根据实际需要,来比较两种或多种方案间的大小关系,选择最佳方案.
解析:由图可知,通话时间为500分钟时,
方案A的费用是230元,
方案B的费用是168元,
∵230>168,∴选择方案B更优惠.
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A. 方案A B. 方案B
C. 两种方案一样优惠 D. 不能确定
B
【当堂检测】
【当堂检测】
2.为深入学习新时代中国特色社会主义思想,中宣部推出“学习强国”学台,学习积分可兑换礼品.某品牌的圆珠笔每支需要40积分,笔芯每支需
要10积分.现积分超市推出以下两种活动:
活动一:按照购买金额打八折扣积分;
活动二:买一支圆珠笔送两支笔芯.
王叔叔有足够的积分,想兑换这种圆珠笔10支,笔芯x支(x≥20).
若只能选择一种兑换活动,请你帮助王叔叔判断选择哪种活动更优惠?
【当堂检测】
解:设活动一的消耗的积分为y1元,活动二的消耗的积分y2,由题意可得,
y1=(40×10+10x)×0.8=8x+320,
当y1=y2时,8x+320=10x+200,
当y1<y2时,8x+320<10x+200,
当y1>y2时,8x+320>10x+200,
∴当x=60时,选择活动一和活动二一样优惠,
当x<60时,选择活动二更优惠.
已知:圆珠笔每支需要40积分,笔芯每支需要10积分.推出以下两种活动:
活动一:按照购买金额打八折扣积分;活动二:买一支圆珠笔送两支笔芯.
问:想兑换这种圆珠笔10支,笔芯x支(x≥20)哪种活动优惠.
y2=40×10+10(x-10×2)=10x+200,
得x=60,
得x>60,
得x<60,
当x>60时,选择活动一更优惠,
三、典型例题
例2.某为支援灾区,某市相关部门组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
甲种货车 乙种货车
载货量(吨/辆) 45 30
租金(元/辆) 400 300
如果计划租用6辆货车,
求出最省钱的租车方案.
分析:根据题意可设租用甲种货车x辆,则租用乙种货车(6-x)辆.根据共募捐了240吨救灾物资,以及每辆货车的载重量得出不等式求解即可,进而根据每辆车的租金求出最省钱的租车方案.
三、典型例题
甲种货车 乙种货车
载货量(吨/辆) 45 30
租金(元/辆) 400 300
解:设租用甲种货车x辆,
则租用乙种货车(6-x)辆.
根据题意,得45x+30(6-x)≥240,
解得x≥4,所以4≤x≤6.
则租车方案共有3种:①租甲种货车4辆,乙种货车2辆;
②租甲种货车5辆,乙种货车1辆;
3种租车方案总费用分别为:①4×400+2×300=2200(元);
②5×400+1×300=2300(元);
∵2400>2300>2200,所以最省钱的租车方案是租用甲种货车4辆,乙种货车2辆.
③租甲种货车6辆,乙种货车0辆.
③6×400=2400(元).
3.某文化用品商店出手书包和文具盒,书包每个定价40元,文具盒每个定价10元,该店制定了两种优惠方案:方案一:买一个书包赠送一个文具盒;方案二:按总价的九折付款.购买时,顾客只能选用其中的一种方案.某学校为给学生发奖品,需购买5个书包,文具盒若干(不少于5个).设文具盒个数为x(个),付款金额为y(元).
(1)分别写出两种优惠方案中y与x之间的表达式:
方案一:y1= ;方案二:y2= .
9x+180
解析:根据方案一,买一个书包赠送一个文具盒;
方案二:按总价的九折付款,即可得出两种优惠方案中y与x之间的关系式
10x+150
【当堂检测】
解:(2)当x=20时,y1=10×20+150=350元,
(2)若购买20个文具盒,比较以上两种方案中哪种更省钱?
解析:将x=20分别代入(1)中解析式,通过计算比较两种方案中哪种更省钱即可.
∵y1<y2
∴方案一更省钱
【当堂检测】
(3)学校计划用540元钱购买这两种奖品,最多可以买到多少个文具盒?
解析:分别求出y≤540时两种方案中x的最大整数值,比较即可得出答案.
当10x+150≤540,解得x≤39;
故学校计划用540元钱购买这两种奖品,最多可以买到40个文具盒.
y2=9×20+180=360元
当9x+180≤540,解得x≤40.
【当堂检测】
4.某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.
甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型 B型
价格(万元) 10 8
处理污水量(吨/月) 180 150
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业
有哪几种购买方案.
【当堂检测】
解:(1)设购进A型污水处理设备x台,
则购进B型污水处理设备(10-x)台,
依题意,得:10x+8(10-x)≤85,
解得x≤2.5,
又因为x为非负整数,所以x=0,1,2.
所以该企业有三种购买方案,方案1:购进B型污水处理设备10台;
方案2:购进A型污水处理设备1台,B型污水处理设备9台;
方案3:购进A型污水处理设备2台,B型污水处理设备8台.
A型 B型
价格(万元) 10 8
处理污水量 (吨/月) 180 150
【当堂检测】
A型 B型
价格(万元) 10 8
处理污水量 (吨/月) 180 150
(2)在(1)的条件下,若每月需要处理
的污水不低于1530吨,为了节约资金,请
你为该企业设计一种最省钱的购买方案.
(2)根据题意,得:180x+150(10-x)≥1530,
解得:x≥1,所以x=1,2.
当x=1时,10-x=9,购买污水处理设备的资金为10×1+8×9=82(万元);
当x=2时,10-x=8,购买污水处理设备的资金为10×2+8×8=84(万元).
所以最省钱的购买方案为:购进A型污水处理设备1台,B型污水处理设备9台.
四、课堂总结
①从数学角度分析实际问题,建立函数模型
1.有关问题:如“方案选择”、“通话优惠”等问题
②列出不等式(方程),求出自变量在不同取值时,对应的函数值大小关系
③结合实际需求,选择最佳方案
用一次函数和一元一次不等式解决实际问题:
2.解题思路及方法:
第二章 一元一次不等式
与一元一次不等式组
2.5 一元一次不等式与一次函数
第2课时
1.能用一次函数和一元一次不等式解决实际问题 (重点)
2.体会不等式、函数、方程的内在联系
一、学习目标
二、新课导入
想一想:
你还记得我们上节课是如何求不等式5x+4<2x+10的解集的吗?
画出直线y1=5x +4,
直线y2=2x +10
x
y
0
2
y2=2x+10
y1=5x+4
不等式的解集为x<2
5x+4 < 2x+10
直线y1 = 5x +4,
直线y2 = 2x +10
比较y1与y2的大小
实际问题
y1<y2
三、典型例题
例1.某商店5月1日举行促销活动,当天到该商店购买商品有两种优惠方案:
方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,
一律按商品价格的8折优惠;
方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5
折优惠.
目标 会利用一次函数和一元一次不等式选择最优方案
三、典型例题
已知小敏5月1日前不是该商店的会员.
(1)若小敏不购买会员卡,当所购买商品的价格为120元时,
实际应支付多少元?
所以实际应支付114元.
解:(1)120×0.95=114(元),
方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,
一律按商品价格的8折优惠;
方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.
三、典型例题
(2)请帮小敏算一算:所购买商品的价格在什么范围内时,采用方案一更合算?
所购买商品的价格在什么范围内时,采用方案二更合算?
(2)设购买商品的价格为x元,
则采用方案一实际应支付(0.8x+168)元,
当0.8x+168<0.95x时,解得x>1120;
当0.8x+168>0.95x时,解得x<1120.
故当购买商品的价格超过1120元时,采用方案一更合算;
当购买商品的价格小于1120元时,采用方案二更合算.
采用方案二实际应支付0.95x元.
三、典型例题
归纳总结:
结合“新课导入”中求不等式5x+4<2x+10的解集,我们知道可以通过比较函数值的大小,求解集.
那么在实际问题中,我们可以根据实际需要,来比较两种或多种方案间的大小关系,选择最佳方案.
解析:由图可知,通话时间为500分钟时,
方案A的费用是230元,
方案B的费用是168元,
∵230>168,∴选择方案B更优惠.
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A. 方案A B. 方案B
C. 两种方案一样优惠 D. 不能确定
B
【当堂检测】
【当堂检测】
2.为深入学习新时代中国特色社会主义思想,中宣部推出“学习强国”学台,学习积分可兑换礼品.某品牌的圆珠笔每支需要40积分,笔芯每支需
要10积分.现积分超市推出以下两种活动:
活动一:按照购买金额打八折扣积分;
活动二:买一支圆珠笔送两支笔芯.
王叔叔有足够的积分,想兑换这种圆珠笔10支,笔芯x支(x≥20).
若只能选择一种兑换活动,请你帮助王叔叔判断选择哪种活动更优惠?
【当堂检测】
解:设活动一的消耗的积分为y1元,活动二的消耗的积分y2,由题意可得,
y1=(40×10+10x)×0.8=8x+320,
当y1=y2时,8x+320=10x+200,
当y1<y2时,8x+320<10x+200,
当y1>y2时,8x+320>10x+200,
∴当x=60时,选择活动一和活动二一样优惠,
当x<60时,选择活动二更优惠.
已知:圆珠笔每支需要40积分,笔芯每支需要10积分.推出以下两种活动:
活动一:按照购买金额打八折扣积分;活动二:买一支圆珠笔送两支笔芯.
问:想兑换这种圆珠笔10支,笔芯x支(x≥20)哪种活动优惠.
y2=40×10+10(x-10×2)=10x+200,
得x=60,
得x>60,
得x<60,
当x>60时,选择活动一更优惠,
三、典型例题
例2.某为支援灾区,某市相关部门组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
甲种货车 乙种货车
载货量(吨/辆) 45 30
租金(元/辆) 400 300
如果计划租用6辆货车,
求出最省钱的租车方案.
分析:根据题意可设租用甲种货车x辆,则租用乙种货车(6-x)辆.根据共募捐了240吨救灾物资,以及每辆货车的载重量得出不等式求解即可,进而根据每辆车的租金求出最省钱的租车方案.
三、典型例题
甲种货车 乙种货车
载货量(吨/辆) 45 30
租金(元/辆) 400 300
解:设租用甲种货车x辆,
则租用乙种货车(6-x)辆.
根据题意,得45x+30(6-x)≥240,
解得x≥4,所以4≤x≤6.
则租车方案共有3种:①租甲种货车4辆,乙种货车2辆;
②租甲种货车5辆,乙种货车1辆;
3种租车方案总费用分别为:①4×400+2×300=2200(元);
②5×400+1×300=2300(元);
∵2400>2300>2200,所以最省钱的租车方案是租用甲种货车4辆,乙种货车2辆.
③租甲种货车6辆,乙种货车0辆.
③6×400=2400(元).
3.某文化用品商店出手书包和文具盒,书包每个定价40元,文具盒每个定价10元,该店制定了两种优惠方案:方案一:买一个书包赠送一个文具盒;方案二:按总价的九折付款.购买时,顾客只能选用其中的一种方案.某学校为给学生发奖品,需购买5个书包,文具盒若干(不少于5个).设文具盒个数为x(个),付款金额为y(元).
(1)分别写出两种优惠方案中y与x之间的表达式:
方案一:y1= ;方案二:y2= .
9x+180
解析:根据方案一,买一个书包赠送一个文具盒;
方案二:按总价的九折付款,即可得出两种优惠方案中y与x之间的关系式
10x+150
【当堂检测】
解:(2)当x=20时,y1=10×20+150=350元,
(2)若购买20个文具盒,比较以上两种方案中哪种更省钱?
解析:将x=20分别代入(1)中解析式,通过计算比较两种方案中哪种更省钱即可.
∵y1<y2
∴方案一更省钱
【当堂检测】
(3)学校计划用540元钱购买这两种奖品,最多可以买到多少个文具盒?
解析:分别求出y≤540时两种方案中x的最大整数值,比较即可得出答案.
当10x+150≤540,解得x≤39;
故学校计划用540元钱购买这两种奖品,最多可以买到40个文具盒.
y2=9×20+180=360元
当9x+180≤540,解得x≤40.
【当堂检测】
4.某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.
甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型 B型
价格(万元) 10 8
处理污水量(吨/月) 180 150
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业
有哪几种购买方案.
【当堂检测】
解:(1)设购进A型污水处理设备x台,
则购进B型污水处理设备(10-x)台,
依题意,得:10x+8(10-x)≤85,
解得x≤2.5,
又因为x为非负整数,所以x=0,1,2.
所以该企业有三种购买方案,方案1:购进B型污水处理设备10台;
方案2:购进A型污水处理设备1台,B型污水处理设备9台;
方案3:购进A型污水处理设备2台,B型污水处理设备8台.
A型 B型
价格(万元) 10 8
处理污水量 (吨/月) 180 150
【当堂检测】
A型 B型
价格(万元) 10 8
处理污水量 (吨/月) 180 150
(2)在(1)的条件下,若每月需要处理
的污水不低于1530吨,为了节约资金,请
你为该企业设计一种最省钱的购买方案.
(2)根据题意,得:180x+150(10-x)≥1530,
解得:x≥1,所以x=1,2.
当x=1时,10-x=9,购买污水处理设备的资金为10×1+8×9=82(万元);
当x=2时,10-x=8,购买污水处理设备的资金为10×2+8×8=84(万元).
所以最省钱的购买方案为:购进A型污水处理设备1台,B型污水处理设备9台.
四、课堂总结
①从数学角度分析实际问题,建立函数模型
1.有关问题:如“方案选择”、“通话优惠”等问题
②列出不等式(方程),求出自变量在不同取值时,对应的函数值大小关系
③结合实际需求,选择最佳方案
用一次函数和一元一次不等式解决实际问题:
2.解题思路及方法:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
