2023-2024学年初中数学北师大版八年级下册6.4 多边形的内角和与外角和第1课时课件(共14张PPT)
文档属性
| 名称 | 2023-2024学年初中数学北师大版八年级下册6.4 多边形的内角和与外角和第1课时课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:44:49 | ||
图片预览





文档简介
(共14张PPT)
第1课时
第六章 平行四边形
6.4 多边形的内角和与外角和
一、学习目标
1.理解多边形内角和公式的概念
2.会用多边形内角和公式解决简单的问题
二、新课导入
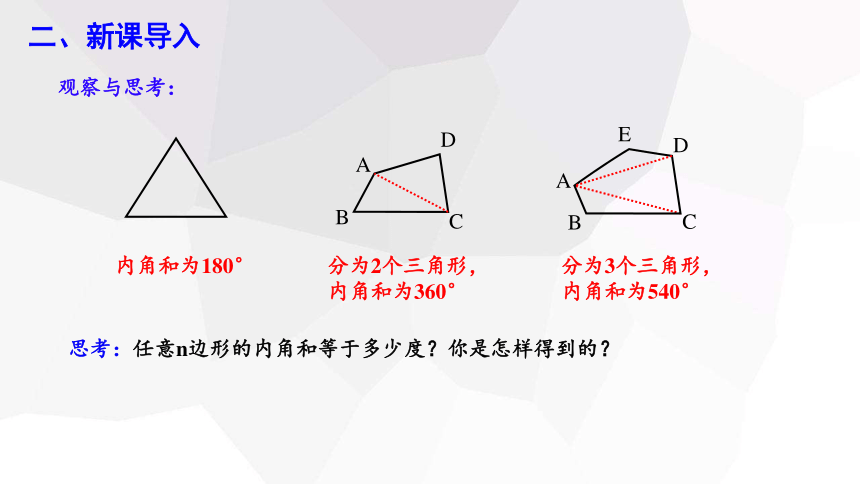
观察与思考:
思考:任意n边形的内角和等于多少度?你是怎样得到的?
内角和为180°
分为2个三角形,
内角和为360°
分为3个三角形,
内角和为540°
A
B
C
D
C
E
A
B
D
例1:小组活动,探索下列问题.
(1)过 n 边形的一个顶点可以作几条对角线?
(2)n边形一共可以作几条对角线?
三、典型例题
(一)多边形的内角和公式
任务分配:
1. 每人分配一个图形,先过一个顶点画出所有对角线;
2.在表格中填出相应的数据;
2. 小组交流并汇总完成全部表格.
分配图形,画出对角线:
A
B
C
D
E
A
B
C
D
A
B
C
D
F
E
多边形的边数 4 5 6 …… n
从一个顶点出发 对角线的条数 ……
对角线的总条数 ……
1
2
3
2
5
9
n – 3
填数据:
……
思考:对角线的条数与分成的三角形的个数、多边形的内角和有什么关系?
三、典型例题
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
n 边形
六边形
五边形
四边形
三角形
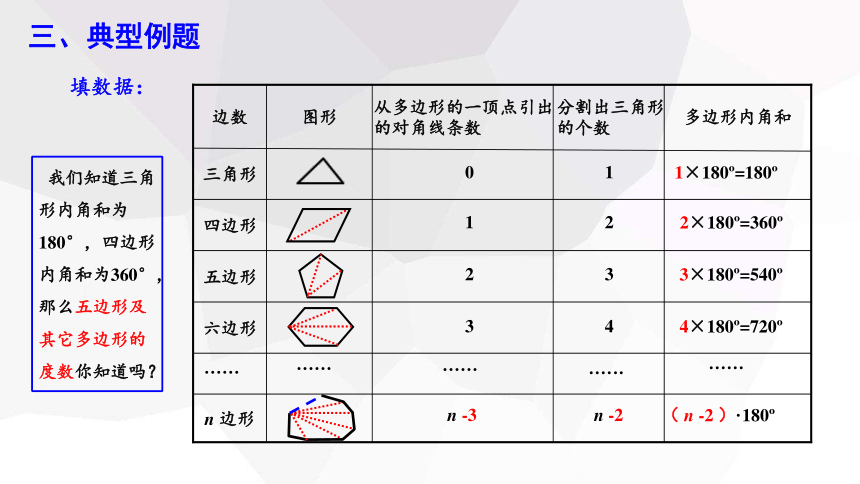
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
填数据:
我们知道三角形内角和为180°,四边形内角和为360°,那么五边形及其它多边形的度数你知道吗?
三、典型例题
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们
将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2) .
﹙n为不小于3的整数﹚
归纳总结
注意:n 边形一共有 条对角线.
三、典型例题
【当堂检测】
1. 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和
相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
B
(3) 多边形的边数每多一条,它的内角和就增加 .
【当堂检测】
2. (1)从七边形的一个顶点出发最多画出几条对角线 ;一个七边形的
所有对角线有 条.
4
14
(2) 已知一个多边形,它的内角和 等于720°,它是一个 边形.
180°
提示:结合n边形的对角线规律及内角和公式即可得出答案.
解: (2)设多边形的边数为n,结合内角和公式可得
(n-2) 180°= 720 .
解得n=6
它是一个六边形.
六
(3)由(n-2) 180°可知,每增加一条边,内角和就增加180°.
例2. (1)如图,在四边形ABCD中,∠A+∠C=180°,∠B 与∠D有怎样的关系
解:∠B 与∠D互补.
∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
结论:如果四边形一组对角互补,
那么另一组对角也互补.
三、典型例题
(二)多边形的内角和公式的应用
例2. (2)剪掉一张长方形纸片的一个角后,纸片还剩下几个角?其内角和是多少度?
提示:注意剪去的位置.
解:由题意知,当去掉一个角后,可分为以下三种情况:
三角形内角和为180°
②如图2,还剩下4个角:
四边形的内角和为360°
③如图3,还剩下5个角:
图1
图2
五边形的内角和为540°
图3
归纳:一个多边形截去一个角后,边数可能
增加一条,也可能不变或减少一条.
三、典型例题
①如图1,还剩下3个角:
【当堂检测】
3. 刘师傅把一个六边形的木板锯掉一个角,那么剩下的木板的形状不可能是 ( )
A.四边形 B.五边形 C.六边形 D.七边形
A
4. 下面不可能是多边形内角和的是 ( )
A.360° B. 540° C. 600° D. 720°
C
点拨:多边形的内角和一定为180°的正整数倍.
【当堂检测】
5. (1)若n边形的内角和是144n°,求n的值 .
(2)已知一个多边形的每一个内角都是156°,求它的边数.
解:(1)由多边形的内角和公式可得:
(n - 2) · 180°= 144n°
解得n = 10.
(2)设多边形的边数为n,由多边形的内角和公式可得:
(n - 2) · 180°=156° · n
解得n = 15.
注意:正n边形的内角相等,每一个
内角是 度.
四、课堂总结
2.多边形的内角和公式为: .
(n-2)×180°
3.正n边形的内角 ,内角和公式为: .
相等
(n-3)
(n-2)
1.由n边形的一个顶点可以引 条对角线,将n边形分成 个
三角形.
第1课时
第六章 平行四边形
6.4 多边形的内角和与外角和
一、学习目标
1.理解多边形内角和公式的概念
2.会用多边形内角和公式解决简单的问题
二、新课导入
观察与思考:
思考:任意n边形的内角和等于多少度?你是怎样得到的?
内角和为180°
分为2个三角形,
内角和为360°
分为3个三角形,
内角和为540°
A
B
C
D
C
E
A
B
D
例1:小组活动,探索下列问题.
(1)过 n 边形的一个顶点可以作几条对角线?
(2)n边形一共可以作几条对角线?
三、典型例题
(一)多边形的内角和公式
任务分配:
1. 每人分配一个图形,先过一个顶点画出所有对角线;
2.在表格中填出相应的数据;
2. 小组交流并汇总完成全部表格.
分配图形,画出对角线:
A
B
C
D
E
A
B
C
D
A
B
C
D
F
E
多边形的边数 4 5 6 …… n
从一个顶点出发 对角线的条数 ……
对角线的总条数 ……
1
2
3
2
5
9
n – 3
填数据:
……
思考:对角线的条数与分成的三角形的个数、多边形的内角和有什么关系?
三、典型例题
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
填数据:
我们知道三角形内角和为180°,四边形内角和为360°,那么五边形及其它多边形的度数你知道吗?
三、典型例题
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们
将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2) .
﹙n为不小于3的整数﹚
归纳总结
注意:n 边形一共有 条对角线.
三、典型例题
【当堂检测】
1. 如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和
相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
B
(3) 多边形的边数每多一条,它的内角和就增加 .
【当堂检测】
2. (1)从七边形的一个顶点出发最多画出几条对角线 ;一个七边形的
所有对角线有 条.
4
14
(2) 已知一个多边形,它的内角和 等于720°,它是一个 边形.
180°
提示:结合n边形的对角线规律及内角和公式即可得出答案.
解: (2)设多边形的边数为n,结合内角和公式可得
(n-2) 180°= 720 .
解得n=6
它是一个六边形.
六
(3)由(n-2) 180°可知,每增加一条边,内角和就增加180°.
例2. (1)如图,在四边形ABCD中,∠A+∠C=180°,∠B 与∠D有怎样的关系
解:∠B 与∠D互补.
∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
结论:如果四边形一组对角互补,
那么另一组对角也互补.
三、典型例题
(二)多边形的内角和公式的应用
例2. (2)剪掉一张长方形纸片的一个角后,纸片还剩下几个角?其内角和是多少度?
提示:注意剪去的位置.
解:由题意知,当去掉一个角后,可分为以下三种情况:
三角形内角和为180°
②如图2,还剩下4个角:
四边形的内角和为360°
③如图3,还剩下5个角:
图1
图2
五边形的内角和为540°
图3
归纳:一个多边形截去一个角后,边数可能
增加一条,也可能不变或减少一条.
三、典型例题
①如图1,还剩下3个角:
【当堂检测】
3. 刘师傅把一个六边形的木板锯掉一个角,那么剩下的木板的形状不可能是 ( )
A.四边形 B.五边形 C.六边形 D.七边形
A
4. 下面不可能是多边形内角和的是 ( )
A.360° B. 540° C. 600° D. 720°
C
点拨:多边形的内角和一定为180°的正整数倍.
【当堂检测】
5. (1)若n边形的内角和是144n°,求n的值 .
(2)已知一个多边形的每一个内角都是156°,求它的边数.
解:(1)由多边形的内角和公式可得:
(n - 2) · 180°= 144n°
解得n = 10.
(2)设多边形的边数为n,由多边形的内角和公式可得:
(n - 2) · 180°=156° · n
解得n = 15.
注意:正n边形的内角相等,每一个
内角是 度.
四、课堂总结
2.多边形的内角和公式为: .
(n-2)×180°
3.正n边形的内角 ,内角和公式为: .
相等
(n-3)
(n-2)
1.由n边形的一个顶点可以引 条对角线,将n边形分成 个
三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
