3.2 图形的旋转 课件(2课时,共26张PPT) 2023-2024学年初中数学北师大版八年级下册
文档属性
| 名称 | 3.2 图形的旋转 课件(2课时,共26张PPT) 2023-2024学年初中数学北师大版八年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:41:58 | ||
图片预览




文档简介
(共26张PPT)
第三章 图形的平移与旋转
第1课时
3.2 图形的旋转
1.掌握旋转的定义
2.熟记旋转的基本性质
一、学习目标
二、新课导入
钟表的指针和摩天轮在做什么运动?
三、概念剖析
(一)旋转的概念
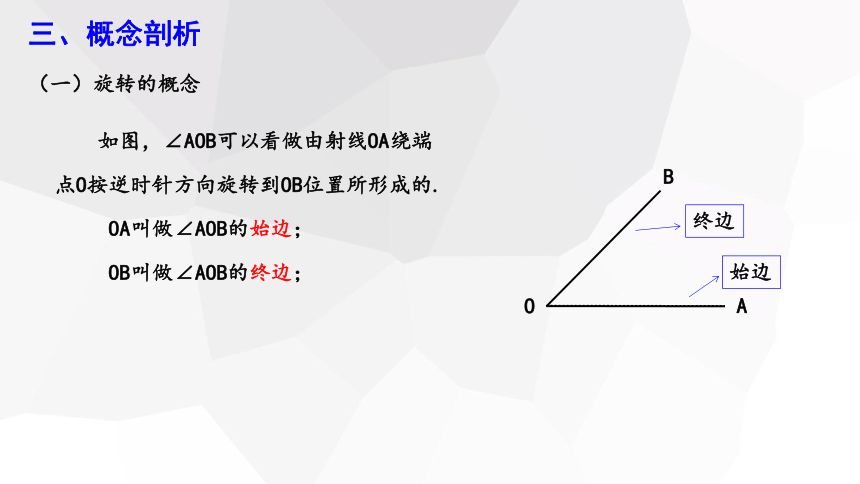
如图,∠AOB可以看做由射线OA绕端点O按逆时针方向旋转到OB位置所形成的.
OA叫做∠AOB的始边;
OB叫做∠AOB的终边;
O
A
B
始边
终边
三、概念剖析
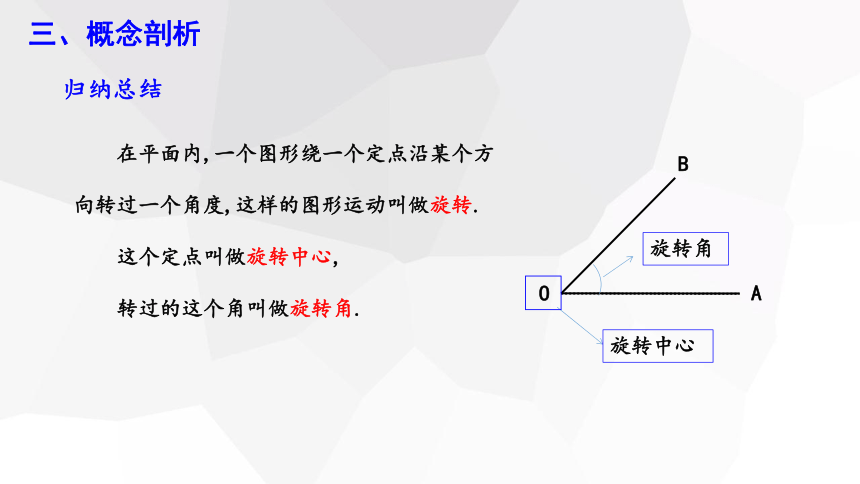
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.
这个定点叫做旋转中心,
转过的这个角叫做旋转角.
归纳总结
O
A
B
旋转角
旋转中心
三、概念剖析
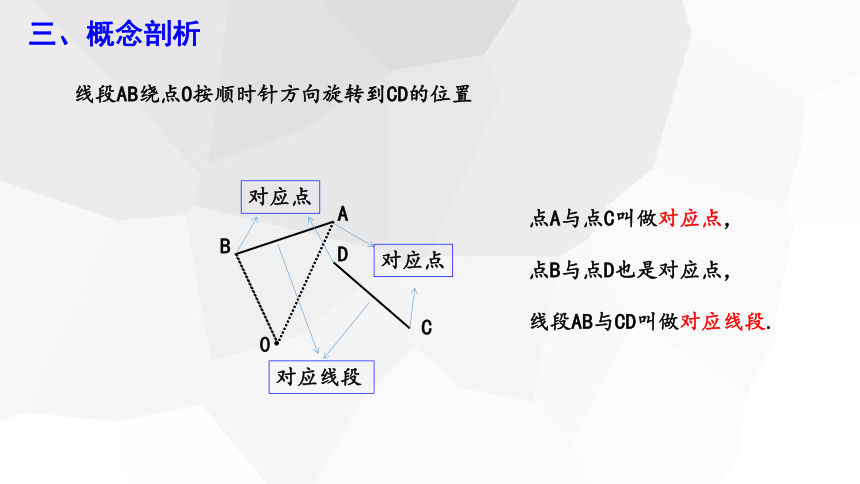
线段AB绕点O按顺时针方向旋转到CD的位置
A
B
0
.
D
C
点A与点C叫做对应点,
点B与点D也是对应点,
线段AB与CD叫做对应线段.
对应点
对应点
对应线段
三、概念剖析
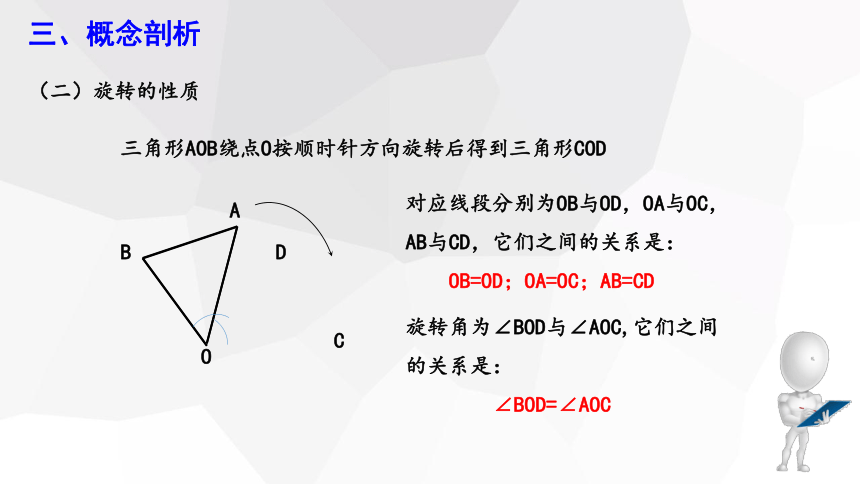
三角形AOB绕点O按顺时针方向旋转后得到三角形COD
(二)旋转的性质
O
B
A
D
C
对应线段分别为OB与OD,OA与OC,AB与CD,它们之间的关系是:
OB=OD;OA=OC;AB=CD
旋转角为∠BOD与∠AOC,它们之间的关系是:
∠BOD=∠AOC
三、概念剖析
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
归纳总结
四、典型例题
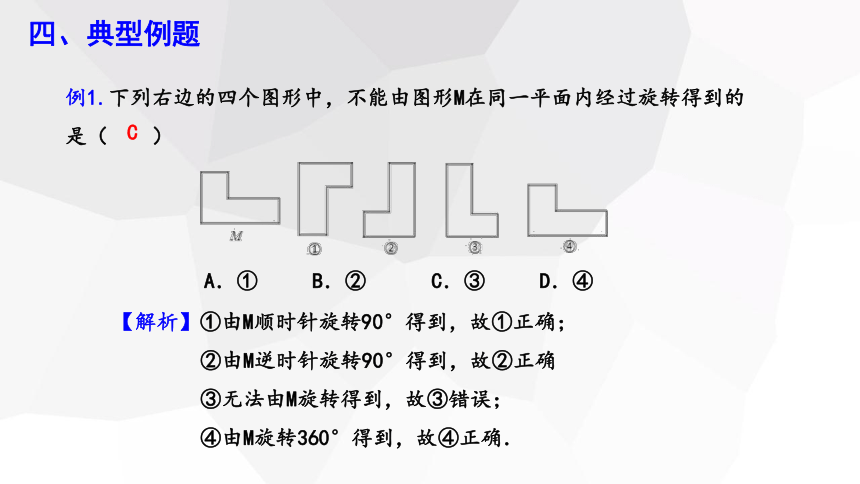
例1.下列右边的四个图形中,不能由图形M在同一平面内经过旋转得到的是( )
C
【解析】①由M顺时针旋转90°得到,故①正确;
②由M逆时针旋转90°得到,故②正确
③无法由M旋转得到,故③错误;
④由M旋转360°得到,故④正确.
A.① B.② C.③ D.④
【当堂检测】
1.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友
B.正在走动的时针
C.骑自行车的人
D.正在转动的风车叶片
C
注意:本题主要考查了生活中的旋转现象,解题的关键是要正确理解旋转的特征:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;
四、典型例题
例2.如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
解:根据旋转的性质可得:
AC与AB是对应边,∠BAC=∠BAP+∠PAC=60°,
∵∠PAC=20°,
∴∠CAE=∠BAP=40°,
∴∠BAE=∠BAC+∠CAE
=60°+40°=100°.
【当堂检测】
2.如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
D
A.60° B.90°
C.120° D.150°
【当堂检测】
3.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
解:∵△ABC绕点C顺时针方向旋转40°得△A′B′C′,
∴∠ACA′=40°,∠A=∠A′(∠BAC),
∵AC⊥A′B′,
∴∠A′=90°-40°=50°,
∴∠BAC=50°.
五、课堂总结
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.
这个定点叫做旋转中心,
转过的这个角叫做旋转角.
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
1.旋转的概念
2.旋转的性质
第三章 图形的平移与旋转
第2课时
3.2 图形的旋转
1.掌握简单平面图形旋转的作法
2.能运用平移、旋转分析两个图形之间的变化过程
一、学习目标
二、新课导入
复习回顾:
1.“旋转”的定义:
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
2.“旋转”的基本性质:
(1)经过旋转,图形的形状和大小不变;
(2)经过旋转,图形上的每一点都绕旋转中心沿相同的方向转动了相同的角度;
(3)任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
三、概念剖析
观察下列动画:将“小旗子”绕点O按顺时针方向旋转90°后,图形有什么变化?
知识点:旋转作图
O
旋转90°后,图形形状和大小没有变化,只有位置发生变化.
问题1:经过旋转,OA与OA′的关系是 .
问题2:∠AOA′是什么角?它是多少度?
OA=OA′
∠AOA′是旋转角
∠AOA′=90°
A
A ′
讨论:要画出旋转后的“小旗子”需要确定哪些条件?
先要确定旋转中心,其次确定旋转方向,最后确定旋转角度.
三、概念剖析
想一想:图中的A与对应点A′、OA与对应线段OA′是如何确定的?你知道确定它们的依据是什么吗?
O
A
A ′
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′=OA;
(4) 点A ′就是点A的旋转对应点.
确定对应点的依据是旋转的基本性质.
四、典型例题
例1.按要求作图,在下面的网格中,已知△ABC的顶点分别落在网格的格点,点A′、C′分别是点A、C两点绕某一点O旋转同样的角度后的对应点
解:(1)旋转中心O的位置如图所示:
.
O
分析:根据旋转的性质,连接对应点AA′、CC′,作它们的垂直平分线的交点即为
旋转中心O.
(1)请在下图中作出旋转中心O的位置;
四、典型例题
(2)点A′是点A绕点O旋转多少度形成的;
(3)画出△ABC绕点O旋转同样的角度后的△A′B′C′.
(2)看图可知,点A′是点A绕点O旋转90度形成的,故答案为90°;
(3)找到B′的位置,然后顺次连接即可.
△A′B′C′如图所示;
.
O
B'
“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:找出构成图形的关键点 (比如线段的两个端点、三角形的三个顶点等);
(3)旋转关键点:
沿一定的方向和角度分别作出各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形.
归纳:
四、典型例题
1.在方格纸上作出“小旗子”绕点O按顺时针旋转90°后的图案.
O
A
A ′
B
B ′
C
C ′
【当堂检测】
【当堂检测】
2.在边长为1的小正方形组成的网格中,现已知△ABC的三个顶点均在小正方形顶点上,根据下列要求,利用网格完成作图.以点B为中心,将△ABC逆时针旋转90°,得到△A′BC′.
C′
A′
3.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC.
将△ABC绕格点O顺时针旋转90°,得到△A′B′C′,画出△A′B′C′.
【当堂检测】
A′
B′
C′
五、课堂总结
旋转作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形.
第三章 图形的平移与旋转
第1课时
3.2 图形的旋转
1.掌握旋转的定义
2.熟记旋转的基本性质
一、学习目标
二、新课导入
钟表的指针和摩天轮在做什么运动?
三、概念剖析
(一)旋转的概念
如图,∠AOB可以看做由射线OA绕端点O按逆时针方向旋转到OB位置所形成的.
OA叫做∠AOB的始边;
OB叫做∠AOB的终边;
O
A
B
始边
终边
三、概念剖析
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.
这个定点叫做旋转中心,
转过的这个角叫做旋转角.
归纳总结
O
A
B
旋转角
旋转中心
三、概念剖析
线段AB绕点O按顺时针方向旋转到CD的位置
A
B
0
.
D
C
点A与点C叫做对应点,
点B与点D也是对应点,
线段AB与CD叫做对应线段.
对应点
对应点
对应线段
三、概念剖析
三角形AOB绕点O按顺时针方向旋转后得到三角形COD
(二)旋转的性质
O
B
A
D
C
对应线段分别为OB与OD,OA与OC,AB与CD,它们之间的关系是:
OB=OD;OA=OC;AB=CD
旋转角为∠BOD与∠AOC,它们之间的关系是:
∠BOD=∠AOC
三、概念剖析
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;
每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
归纳总结
四、典型例题
例1.下列右边的四个图形中,不能由图形M在同一平面内经过旋转得到的是( )
C
【解析】①由M顺时针旋转90°得到,故①正确;
②由M逆时针旋转90°得到,故②正确
③无法由M旋转得到,故③错误;
④由M旋转360°得到,故④正确.
A.① B.② C.③ D.④
【当堂检测】
1.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友
B.正在走动的时针
C.骑自行车的人
D.正在转动的风车叶片
C
注意:本题主要考查了生活中的旋转现象,解题的关键是要正确理解旋转的特征:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;
四、典型例题
例2.如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
解:根据旋转的性质可得:
AC与AB是对应边,∠BAC=∠BAP+∠PAC=60°,
∵∠PAC=20°,
∴∠CAE=∠BAP=40°,
∴∠BAE=∠BAC+∠CAE
=60°+40°=100°.
【当堂检测】
2.如图所示,将一个含30°角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B′,若点B′、A、C在同一条直线上,则三角板ABC旋转的度数是( )
D
A.60° B.90°
C.120° D.150°
【当堂检测】
3.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
解:∵△ABC绕点C顺时针方向旋转40°得△A′B′C′,
∴∠ACA′=40°,∠A=∠A′(∠BAC),
∵AC⊥A′B′,
∴∠A′=90°-40°=50°,
∴∠BAC=50°.
五、课堂总结
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转.
这个定点叫做旋转中心,
转过的这个角叫做旋转角.
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
对应点到旋转中心的距离相等;每对对应点与旋转中心连线所成的角都是相等的角,它们都等于旋转角.
1.旋转的概念
2.旋转的性质
第三章 图形的平移与旋转
第2课时
3.2 图形的旋转
1.掌握简单平面图形旋转的作法
2.能运用平移、旋转分析两个图形之间的变化过程
一、学习目标
二、新课导入
复习回顾:
1.“旋转”的定义:
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
2.“旋转”的基本性质:
(1)经过旋转,图形的形状和大小不变;
(2)经过旋转,图形上的每一点都绕旋转中心沿相同的方向转动了相同的角度;
(3)任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
三、概念剖析
观察下列动画:将“小旗子”绕点O按顺时针方向旋转90°后,图形有什么变化?
知识点:旋转作图
O
旋转90°后,图形形状和大小没有变化,只有位置发生变化.
问题1:经过旋转,OA与OA′的关系是 .
问题2:∠AOA′是什么角?它是多少度?
OA=OA′
∠AOA′是旋转角
∠AOA′=90°
A
A ′
讨论:要画出旋转后的“小旗子”需要确定哪些条件?
先要确定旋转中心,其次确定旋转方向,最后确定旋转角度.
三、概念剖析
想一想:图中的A与对应点A′、OA与对应线段OA′是如何确定的?你知道确定它们的依据是什么吗?
O
A
A ′
(1) 将关键点A与旋转中心O连接;
(2) 以OA为始边在旋转方向作一个角等于旋转角;
(3) 在角的终边上截取点A′,使OA ′=OA;
(4) 点A ′就是点A的旋转对应点.
确定对应点的依据是旋转的基本性质.
四、典型例题
例1.按要求作图,在下面的网格中,已知△ABC的顶点分别落在网格的格点,点A′、C′分别是点A、C两点绕某一点O旋转同样的角度后的对应点
解:(1)旋转中心O的位置如图所示:
.
O
分析:根据旋转的性质,连接对应点AA′、CC′,作它们的垂直平分线的交点即为
旋转中心O.
(1)请在下图中作出旋转中心O的位置;
四、典型例题
(2)点A′是点A绕点O旋转多少度形成的;
(3)画出△ABC绕点O旋转同样的角度后的△A′B′C′.
(2)看图可知,点A′是点A绕点O旋转90度形成的,故答案为90°;
(3)找到B′的位置,然后顺次连接即可.
△A′B′C′如图所示;
.
O
B'
“旋转”作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:找出构成图形的关键点 (比如线段的两个端点、三角形的三个顶点等);
(3)旋转关键点:
沿一定的方向和角度分别作出各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形.
归纳:
四、典型例题
1.在方格纸上作出“小旗子”绕点O按顺时针旋转90°后的图案.
O
A
A ′
B
B ′
C
C ′
【当堂检测】
【当堂检测】
2.在边长为1的小正方形组成的网格中,现已知△ABC的三个顶点均在小正方形顶点上,根据下列要求,利用网格完成作图.以点B为中心,将△ABC逆时针旋转90°,得到△A′BC′.
C′
A′
3.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC.
将△ABC绕格点O顺时针旋转90°,得到△A′B′C′,画出△A′B′C′.
【当堂检测】
A′
B′
C′
五、课堂总结
旋转作图的步骤 :
(1)明确题目要求:
弄清旋转中心、方向和角度;
(2)分析所作图形:
找出构成图形的关键点;
(3)旋转关键点:
沿一定的方向和角度分别作出各关键点;
(4)作出新图形:
顺次连接各关键点;
(5)写出结论:
说明所作出的图形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
