第四章《三角形》单元检测试卷（含解析）

中小学教育资源及组卷应用平台
第四章《三角形》单元检测试卷（含解析）
选择题（本大题共有10个小题，每小题4分，共40分）
1．以下列各组线段长为边，能组成三角形的是（　 　）
A．1cm，2cm，4cm B．8cm，6cm，4cm
C．12cm，5cm，6cm D．2cm，3cm，6cm
小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，
他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（　 　）
A．① B．② C．③ D．①和②
如图，为估计池塘岸边A，B的距离，小明在池塘的一侧选取一点O，
测得OA=15米，OB=10米，A，B间的距离可能是（　 　）
A．30米 B．25米 C．20米 D．5米
4．如图，∠BAC=90°，AD⊥BC，则图中互余的角有（　 　）
A．2对 B．3对 C．4对 D．5对
5．下面四个图形中，线段BE是⊿ABC的高的图是（　 　）
A． B．
C． D．
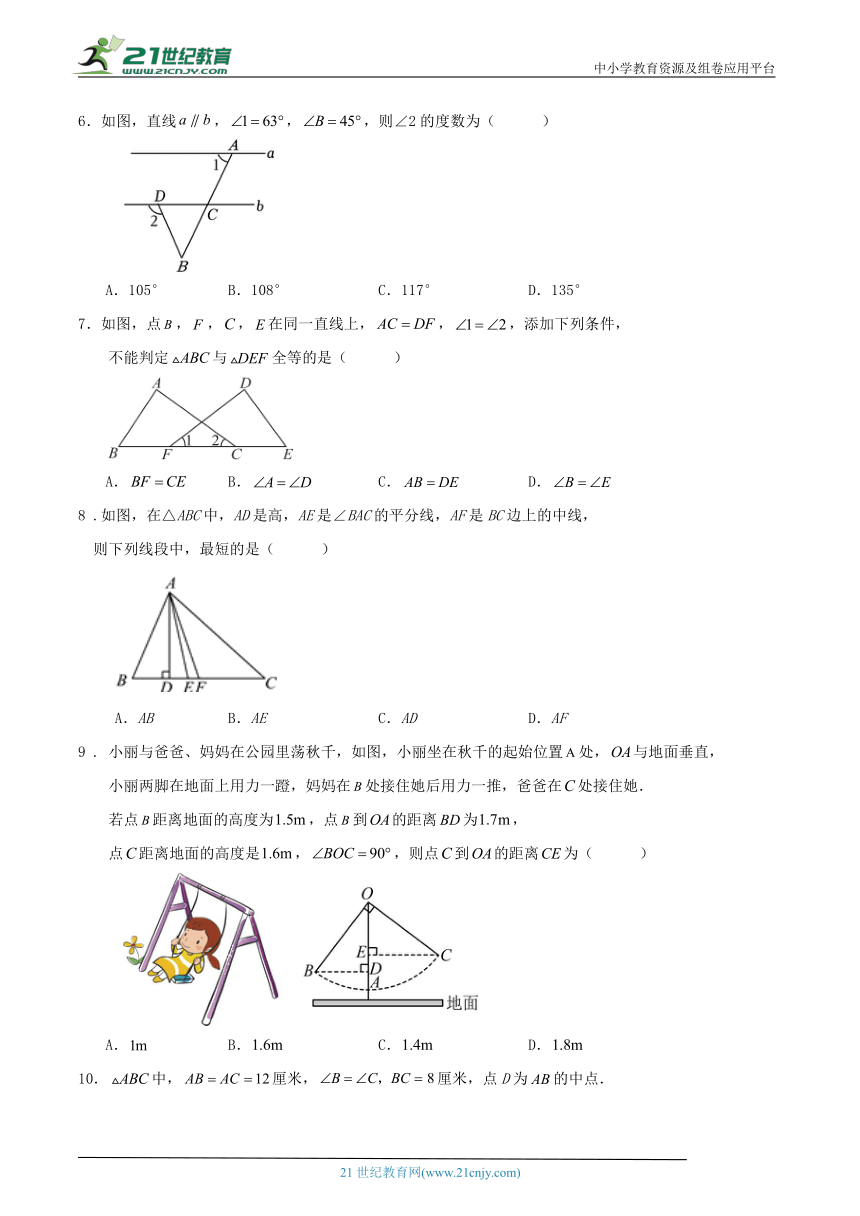
6．如图，直线，，，则∠2的度数为（　 　）
A．105° B．108° C．117° D．135°
如图，点，，，在同一直线上，，，添加下列条件，
不能判定与全等的是（　 　）
A． B． C． D．
8 .如图，在△ABC中，AD是高，AE是∠BAC的平分线，AF是BC边上的中线，
则下列线段中，最短的是（　 　）
A．AB B．AE C．AD D．AF
9 . 小丽与爸爸、妈妈在公园里荡秋千，如图，小丽坐在秋千的起始位置处，与地面垂直，
小丽两脚在地面上用力一蹬，妈妈在处接住她后用力一推，爸爸在处接住她．
若点距离地面的高度为，点到的距离为，
点距离地面的高度是，，则点到的距离为（　 　）
A． B． C． D．
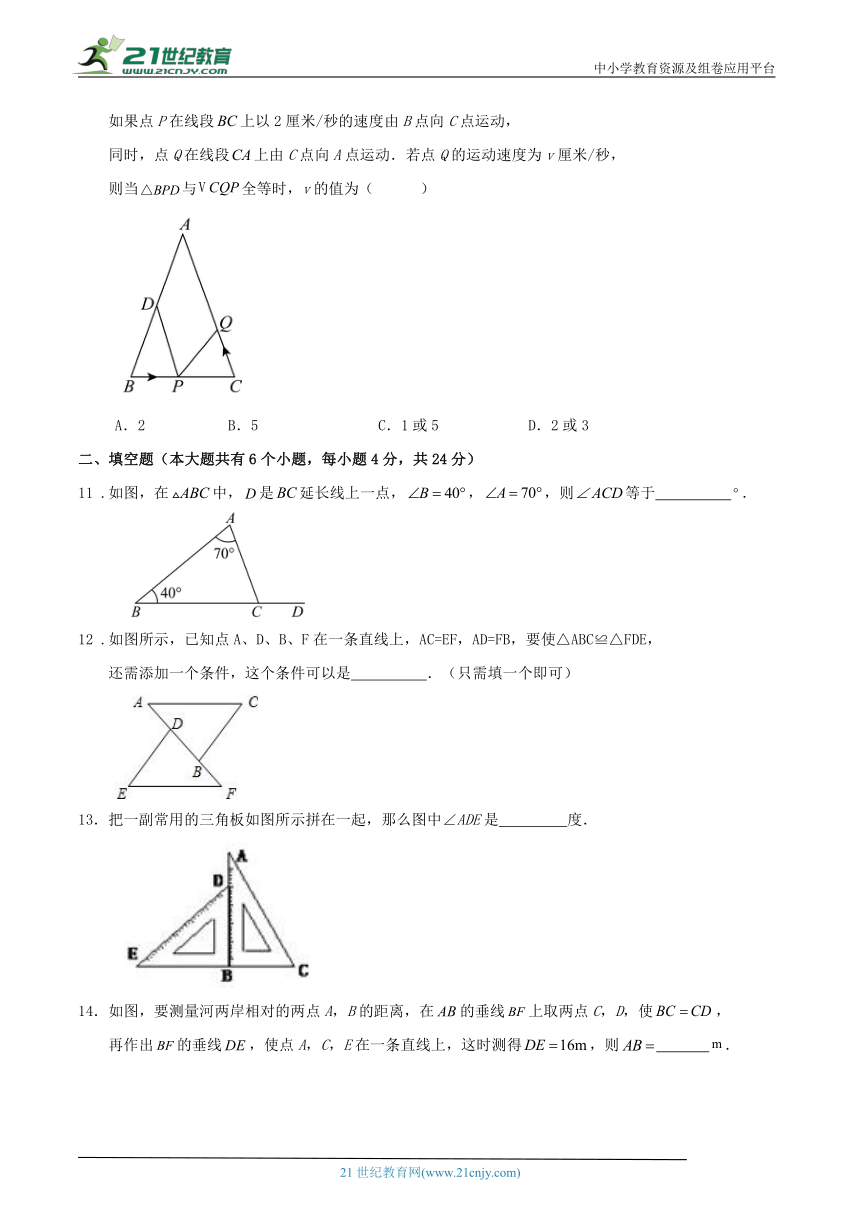
中，厘米，厘米，点D为的中点．
如果点P在线段上以2厘米/秒的速度由B点向C点运动，
同时，点Q在线段上由C点向A点运动．若点Q的运动速度为v厘米/秒，
则当与全等时，v的值为（　 　）
A．2 B．5 C．1或5 D．2或3
填空题（本大题共有6个小题，每小题4分，共24分）
11 .如图，在中，是延长线上一点，，，则等于 ．
12 .如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，
还需添加一个条件，这个条件可以是 ．（只需填一个即可）
13．把一副常用的三角板如图所示拼在一起，那么图中∠ADE是 度．
如图，要测量河两岸相对的两点A，B的距离，在的垂线上取两点C，D，使，
再作出的垂线，使点A，C，E在一条直线上，这时测得，则 ．
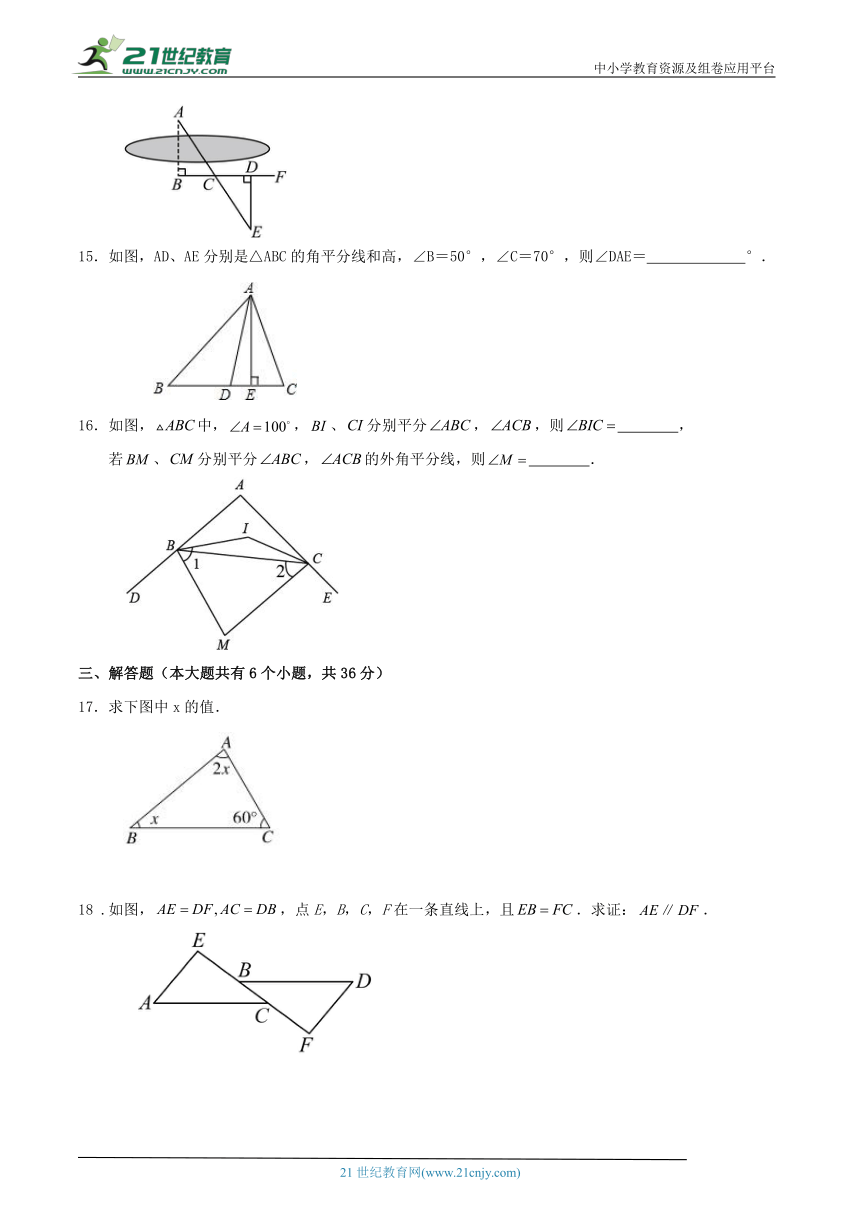
15．如图，AD、AE分别是△ABC的角平分线和高，∠B＝50°，∠C＝70°，则∠DAE＝ °．
如图，中，，、分别平分，，则 ，
若、分别平分，的外角平分线，则 ．
三、解答题（本大题共有6个小题，共36分）
17．求下图中x的值．
18 .如图，，点E，B，C，F在一条直线上，且．求证：．

19.在△ABC中，已知∠B=50°，∠C=60°，AE⊥BC于E，AD平分∠BAC；求：∠DAE的度数．
20．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．
（1）求证：BD=CE；
（2）求证：∠M=∠N．
21 .已知：如图，AB⊥AE，AD⊥AC，∠B＝∠E，CB＝DE．
（1）求证：△ABC≌△AED；
（2）求证：CB⊥DE．
22 . 如图，已知点O是△ABC的两条角平分线的交点，
（1）若∠A=30°，则∠BOC的大小是________；
（2）若∠A=60°，则∠BOC的大小是________；
（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．
第四章《三角形》单元检测试卷 解析
一、选择题（本大题共有10个小题，每小题4分，共40分）
1．以下列各组线段长为边，能组成三角形的是（　 　）
A．1cm，2cm，4cm B．8cm，6cm，4cm
C．12cm，5cm，6cm D．2cm，3cm，6cm
【答案】B
【分析】根据三角形任意两边的和大于第三边，进行分析判断.
【详解】解：A、1+2<4，不能组成三角形；
B、４+6>8，能组成三角形；
C、5+6<11，不能够组成三角形；
D、2+3＜5，不能组成三角形.
故选B.
小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，
他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（　 　）
A．① B．② C．③ D．①和②
【答案】C
【分析】已知三角形破损部分的边角，得到原来三角形的边角，根据三角形全等的判定方法，即可求解．
【详解】第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；
第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA来配一块一样的玻璃.
故选C.
3 .如图，为估计池塘岸边A，B的距离，小明在池塘的一侧选取一点O，
测得OA=15米，OB=10米，A，B间的距离可能是（　 　）
A．30米 B．25米 C．20米 D．5米
【答案】C
【详解】设A，B间的距离为x．
根据三角形的三边关系定理，得：15-10＜x＜15+10，
解得：5＜x＜25，
所以，A，B之间的距离可能是20m．
故选C．
4．如图，∠BAC=90°，AD⊥BC，则图中互余的角有（　 　）
A．2对 B．3对 C．4对 D．5对
【答案】C
【分析】直接利用直角三角形两锐角之和等于90°即可得到答案.
【详解】解：∵∠BAC=90°，
∴∠B+∠A=90°，
∠BAD+∠CAD=90°，
又∵AD⊥BC，
∴∠B+∠BAD=90°，
∠C+∠CAD=90°，
综上，共有4对互余的角.
故选C.
5．下面四个图形中，线段BE是⊿ABC的高的图是（　 　）
A． B．
C． D．
【答案】A
【详解】解：根据三角形高线的定义，只有A选项符合．
故选A．
6．如图，直线，，，则∠2的度数为（　 　）
A．105° B．108° C．117° D．135°
【答案】B
【分析】本题主要考查了平行线的性质，三角形外角的性质，先根据平行线的性质得到，再由三角形外角的性质即可求出答案．
【详解】解：∵，，
∴，
又∵，
∴．
故选：B．
7 .如图，点，，，在同一直线上，，，添加下列条件，
不能判定与全等的是（　 　）
A． B． C． D．
【答案】C
【分析】本题考查全等三角形的判定，根据全等三角形的判定定理(、、、)逐项判断即可．
【详解】解：A、∵
∴，即，
∵，，
∴，故选项A不符合题意；
B、∵，，，
∴，故选项B不符合题意；
C、∵，，，，
∴不能证明，故选项C符合题意；
D、∵，，，
∴，故选项D不符合题意，
故选：C．
8 .如图，在△ABC中，AD是高，AE是∠BAC的平分线，AF是BC边上的中线，
则下列线段中，最短的是（　 　）
A．AB B．AE C．AD D．AF
【答案】C
【分析】首先根据三角形的高的定义得出AD⊥BC，再根据垂线段最短求解即可
【详解】解：∵在△ABC中，AD是高，
∴AD⊥BC，
又∵在△ABC中，AE是∠BAC的平分线，AF是BC边上的中线，
∴AD＜AB，AD＜AE，AD＜AF，
故选C.
9 . 小丽与爸爸、妈妈在公园里荡秋千，如图，小丽坐在秋千的起始位置处，与地面垂直，
小丽两脚在地面上用力一蹬，妈妈在处接住她后用力一推，爸爸在处接住她．
若点距离地面的高度为，点到的距离为，
点距离地面的高度是，，则点到的距离为（　 　）
A． B． C． D．
【答案】D
【分析】本题考查了全等三角形的判定与性质的应用，由证明得出，即可推出结果．
【详解】解：点距离地面的高度为，点距离地面的高度是，
点距离地面的高度为，点距离地面的高度是，
，
，
，
，
又由题意可知，，
，
，，
，
点到的距离为，
故选：D．
10 .中，厘米，厘米，点D为的中点．
如果点P在线段上以2厘米/秒的速度由B点向C点运动，
同时，点Q在线段上由C点向A点运动．若点Q的运动速度为v厘米/秒，
则当与全等时，v的值为（　 　）
A．2 B．5 C．1或5 D．2或3
【答案】D
【分析】本题主要考查了全等三角形的判定，此题要分两种情况：①当时，与全等，计算出的长，进而可得运动时间，然后再求v；②当时，，计算出的长，进而可得运动时间，然后再求v．
【详解】解：当时，与全等，
∵点D为的中点，
∴，
∵，
∴，
∵点P在线段上以2厘米/秒的速度由B点向C点运动，
∴运动时间时,
∵，
∴,
∴；
当时，，
∵，
∴，
∵，
∴,
∴运动时间为，
∴．
故v的值为2或3．
故选：．
二、填空题（本大题共有6个小题，每小题4分，共24分）
11 .如图，在中，是延长线上一点，，，则等于 ．
【答案】
【分析】本题主要考查了三角形外角的性质，根据三角形的一个外角等于与它不相邻的两个内角之和即可求解．
【详解】解：∵，，
∴，
故答案为：．
12 .如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，
还需添加一个条件，这个条件可以是 ．（只需填一个即可）
【答案】∠A=∠F（答案不唯一）
【详解】要判定△ABC≌△FDE，已知AC=FE，AD=BF，则AB=CF，具备了两组边对应相等，故添加夹角∠A=∠F，利用SAS可证全等；或添加AC∥EF得夹角∠A=∠F，利用SAS可证全等；或添加BC=DE，利用SSS可证全等．
13．把一副常用的三角板如图所示拼在一起，那么图中∠ADE是 度．
【答案】135
【分析】看图得△DEB为等腰直角三角形的三角板，得∠EDB的度数，由∠ADB为平角，进而求出∠ADE的度数．
【详解】∵∠EDB=45°，∠ADB=180°，
∴∠ADE=135°．
故答案为：135
14 .如图，要测量河两岸相对的两点A，B的距离，在的垂线上取两点C，D，使，
再作出的垂线，使点A，C，E在一条直线上，这时测得，则 ．
【答案】
【分析】本题主要考查了全等三角形的性质与判定，证明，即可得到．
【详解】解：∵，
∴，
又∵，
∴，
∴，
故答案为；．
15．如图，AD、AE分别是△ABC的角平分线和高，∠B＝50°，∠C＝70°，则∠DAE＝ °．
【答案】10
【分析】根据三角形内角和定理求出∠BAC，再根据角平分线的定义求出∠BAD，根据直角三角形两锐角互余求出∠BAE，然后求解即可．
【详解】解：∵∠B=50°，∠C=70°，
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°，
∵AD是角平分线，
∴∠BAD=∠BAC=×60°=30°，
∵AE是高，
∴∠BAE=90°-∠B=90°-50°=40°，
∴∠DAE=∠BAE-∠BAD=40°-30°=10°．
故答案为：10．
16 .如图，中，，、分别平分，，则 ，
若、分别平分，的外角平分线，则 ．
【答案】
【分析】首先根据三角形内角和求出∠ABC+∠ACB的度数，再根据角平分线的性质得到∠IBC=∠ABC，∠ICB=∠ACB，求出∠IBC+∠ICB的度数，再次根据三角形内角和求出∠I的度数即可；
根据∠ABC+∠ACB的度数，算出∠DBC+∠ECB的度数，然后再利用角平分线的性质得到∠1=∠DBC，∠2=ECB，可得到∠1+∠2的度数，最后再利用三角形内角和定理计算出∠M的度数．
【详解】∵∠A=100°．
∵∠ABC+∠ACB=180°﹣100°=80°．
∵BI、CI分别平分∠ABC，∠ACB，
∴∠IBC=∠ABC，∠ICB=∠ACB，
∴∠IBC+∠ICB=∠ABC+∠ACB=（∠ABC+∠ACB）=×80°=40°，
∴∠I=180°﹣（∠IBC+∠ICB）=180°﹣40°=140°；
∵∠ABC+∠ACB=80°，
∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣（∠ABC+∠ACB）=360°﹣80°=280°．
∵BM、CM分别平分∠ABC，∠ACB的外角平分线，
∴∠1=∠DBC，∠2=ECB，
∴∠1+∠2=×280°=140°，
∴∠M=180°﹣∠1﹣∠2=40°．
故答案为140°；40°．
三、解答题（本大题共有6个小题，共36分）
17．求下图中x的值．
【答案】x＝40°.
【分析】根据三角形的内角和定理可得方程x＋2x＋60°＝180°，解方程求得x的值即可.
【详解】根据三角形的内角和定理可得，
x＋2x＋60°＝180°，
解得x＝40°.
18 .如图，，点E，B，C，F在一条直线上，且．求证：．

解：证明：，
，
即，
在与中，
，
，
，
．
19.在△ABC中，已知∠B=50°，∠C=60°，AE⊥BC于E，AD平分∠BAC；求：∠DAE的度数．
【答案】∠DAE=5°．
【详解】试题分析：根据三角形内角和定理求出∠BAC的度数，再根据角平分线的定义求得∠CAD的度数；在△AEC中，求出∠CAE的度数，从而可得∠DAE的度数．
试题解析：
∵在△ABC中，∠B=50°，∠C=60°，
∴∠BAC=180°﹣50°﹣60°=70°．
∵AD平分∠BAC，
∴∠CAD=∠BAC=35°．
∵AE⊥BC于E，
∴∠CAE=90°﹣60°=30°，
∴∠DAE=∠CAD﹣∠CAE=35°﹣30°=5°．
20．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．
（1）求证：BD=CE；
（2）求证：∠M=∠N．
【答案】（1）见解析；（2）见解析
【分析】（1）根据全等三角形的判定证明△ABD≌△ACE（SAS）即可；
（2）由△ABD≌△ACE证得∠B=∠C，进而证得△ACM≌△ABN（ASA），再根据全等三角形的性质可证得结论．
【详解】（1）证明：在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS），
∴BD=CE；
（2）证明：∵∠1=∠2，
∴∠1+∠DAE=∠2+∠DAE，
即∠BAN=∠CAM，
由（1）知：△ABD≌△ACE，
∴∠B=∠C，
在△ACM和△ABN中，
，
∴△ACM≌△ABN（ASA），
∴∠M=∠N．
21 .已知：如图，AB⊥AE，AD⊥AC，∠B＝∠E，CB＝DE．
（1）求证：△ABC≌△AED；
（2）求证：CB⊥DE．
【答案】（1）证明见解析；（2）证明见解析；
【分析】（1）根据全等三角形的判定定理AAS可以判定△ACB≌△ADE；
（2）找到两个有对顶角的三角形，然后根据内角和定理证明.
【详解】（1）AB⊥AE，AD⊥AC
在△ABC与△AED中
△ABC≌△AED(AAS)
（2）设DE与AB、CB分别交于点E、F.
在△AEF与△BGF中
22 . 如图，已知点O是△ABC的两条角平分线的交点，
（1）若∠A=30°，则∠BOC的大小是________；
（2）若∠A=60°，则∠BOC的大小是________；
（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．
【答案】（1）105°（2）120°（3）n°+90°.
【详解】试题分析：∠BOC+∠OBC+∠OCB=180°，根据角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，等量代换得到∠BOC+ ∠ABC+∠ACB=180°，根据三角形的内角和定理即可得到结论.
试题解析：
（1）如图，在△ABC中，∠A+∠ABC+∠ACB=180°，
在△BOC中，∠BOC+∠OBC+∠OCB=180°，
∵BO，CO分别是∠ABC和∠ACB的平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴∠BOC+ ∠ABC+∠ACB=180°，
又∵在△ABC中，∠A+∠ABC+∠ACB=180°，
∴∠BOC=∠A+90°=105°；
（2）如图，在△ABC中，∠A+∠ABC+∠ACB=180°，
在△BOC中，∠BOC+∠OBC+∠OCB=180°，
∵BO，CO分别是∠ABC和∠ACB的平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴∠BOC+∠ABC+∠ACB=180°，
又∵在△ABC中，∠A+∠ABC+∠ACB=180°，
∴∠BOC=∠A+90°=120°；
（3）∠BOC=n°+90°，
∵OB、OC是两条角平分线，
∴∠OBC=∠ABC, ∠OCB=∠ACB ，
在△OBC中，∠BOC=180°-（∠OBC+∠OCB）
=180°-（∠ABC+∠ACB）
=180°-（∠ABC+∠ACB）
=180°-（180°-∠A）
=∠A+90°
=n°+90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)