华师大版数学九年级下册 27.4 正多边形和圆 课件(共14张PPT)
文档属性
| 名称 | 华师大版数学九年级下册 27.4 正多边形和圆 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 537.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 09:54:08 | ||
图片预览






文档简介
(共14张PPT)
第27章 圆
27. 4 正多边形和圆
一
学习目标
1.了解正多边形和圆的关系,理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
2.会应用正多边形和圆的有关知识画多边形.
二
重难点
重点:应用正多边形和圆的有关知识计算及画正多边形.
难点:熟练应用正多边形半径和边长、边心距、中心角的关系进行计算.
1.知识回顾
三
教学过程
1.各条边相等,各个角也相等的多边形是正多边形.
2.正多边形是轴对称图形.当边数为偶数时,是中心对称图形,当边数为奇数时,不是中心对称图形.
3.正多边形对称轴都交于一点,这些对称轴是各边的垂直平分线和各内角的平分线.
2.探究新知
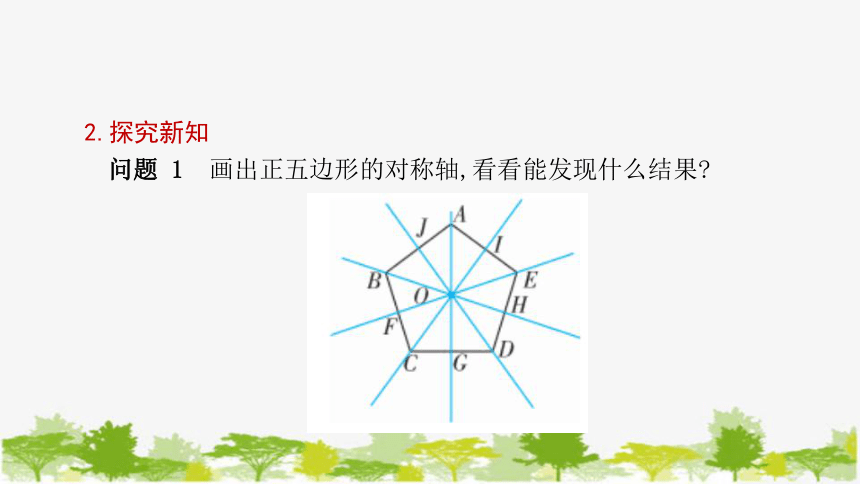
问题 1 画出正五边形的对称轴,看看能发现什么结果
答:(1)我们发现正五边形有五条对称轴,而且这些对称轴都交于一点O.根据轴对称的性质,我们知道这些对称轴是正五边形各边的垂直平分线.
(2)点O到正五边形各个顶点的距离相等,记为R.那么以点O为圆心、R为半径的圆就过正五边形的各个顶点,这个圆是该正五边形的外接圆.
(3)对称轴是正五边形各内角的平分线,根据角平分线的性质,点O到各边的距离都相等,记为r,那么以点O为圆心、r为半径的圆就与正五边形的各条边都相切,这个圆是正五边形的内切圆.
【知识归纳】
1.任何一个正多边形都有一个外接圆与一个内切圆.
2.一个正多边形的外接圆与内切圆有共有的圆心.
3.正多边形的有关概念:
(1)正多边形的中心为外接圆的圆心;
(2)正多边形的半径为外接圆的半径;
(3)正多边形的中心角为正多边形每一边所对的圆心角;
(4)正多边形的边心距为中心到正多边形的一边的距离.
答:在同一个圆中,等弧对等弦,因此AB=BC=CD=DE=EA,而根据圆周角定理,有∠A=∠B=∠C=∠D=∠E,因此五边形ABCDE是正五边形
【知识归纳】
正多边形和圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
3.例题精讲
例 1 如图,有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
例 2 利用尺规作图,作出已知圆的内接正方形.
解:内接正方形的作法:
(1)用直尺任作圆的一条直径AC;
(2)作与直径AC垂直的直径BD;
(3)顺次连结所得的圆上四点,
则四边形ABCD即为所求作的
正方形.(如图)
4.巩固练习 完成教材课后同步练习
5.课堂小结
小结:1.正多边形与圆的关系.
2.正多边形的半径、中心角、边长、边心距的计算及其之间的等量关系.
3.画正多边形的方法.
反思:结合生活中的正多边形的图案,发现正多边形和圆的关系,然后用圆的有关知识,解决正多边形的问题.
第27章 圆
27. 4 正多边形和圆
一
学习目标
1.了解正多边形和圆的关系,理解并掌握正多边形半径和边长、边心距、中心角之间的关系.
2.会应用正多边形和圆的有关知识画多边形.
二
重难点
重点:应用正多边形和圆的有关知识计算及画正多边形.
难点:熟练应用正多边形半径和边长、边心距、中心角的关系进行计算.
1.知识回顾
三
教学过程
1.各条边相等,各个角也相等的多边形是正多边形.
2.正多边形是轴对称图形.当边数为偶数时,是中心对称图形,当边数为奇数时,不是中心对称图形.
3.正多边形对称轴都交于一点,这些对称轴是各边的垂直平分线和各内角的平分线.
2.探究新知
问题 1 画出正五边形的对称轴,看看能发现什么结果
答:(1)我们发现正五边形有五条对称轴,而且这些对称轴都交于一点O.根据轴对称的性质,我们知道这些对称轴是正五边形各边的垂直平分线.
(2)点O到正五边形各个顶点的距离相等,记为R.那么以点O为圆心、R为半径的圆就过正五边形的各个顶点,这个圆是该正五边形的外接圆.
(3)对称轴是正五边形各内角的平分线,根据角平分线的性质,点O到各边的距离都相等,记为r,那么以点O为圆心、r为半径的圆就与正五边形的各条边都相切,这个圆是正五边形的内切圆.
【知识归纳】
1.任何一个正多边形都有一个外接圆与一个内切圆.
2.一个正多边形的外接圆与内切圆有共有的圆心.
3.正多边形的有关概念:
(1)正多边形的中心为外接圆的圆心;
(2)正多边形的半径为外接圆的半径;
(3)正多边形的中心角为正多边形每一边所对的圆心角;
(4)正多边形的边心距为中心到正多边形的一边的距离.
答:在同一个圆中,等弧对等弦,因此AB=BC=CD=DE=EA,而根据圆周角定理,有∠A=∠B=∠C=∠D=∠E,因此五边形ABCDE是正五边形
【知识归纳】
正多边形和圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
3.例题精讲
例 1 如图,有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(结果保留小数点后一位).
例 2 利用尺规作图,作出已知圆的内接正方形.
解:内接正方形的作法:
(1)用直尺任作圆的一条直径AC;
(2)作与直径AC垂直的直径BD;
(3)顺次连结所得的圆上四点,
则四边形ABCD即为所求作的
正方形.(如图)
4.巩固练习 完成教材课后同步练习
5.课堂小结
小结:1.正多边形与圆的关系.
2.正多边形的半径、中心角、边长、边心距的计算及其之间的等量关系.
3.画正多边形的方法.
反思:结合生活中的正多边形的图案,发现正多边形和圆的关系,然后用圆的有关知识,解决正多边形的问题.
