1.5《组合图形的面积》(教学课件)(共28张PPT)三年级+数学下册+沪教版
文档属性
| 名称 | 1.5《组合图形的面积》(教学课件)(共28张PPT)三年级+数学下册+沪教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
组合图形的面积
小学数学·三年级(下)
沪教版·第一单元
明确组合图形的意义,掌握用分解法或添补法求组合图形的面积。
能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
渗透转化的教学思想,提高学生运用新知识解决实际问题的能力,在自主探索活动中培养创新精神。
重
择有效的计算方法解决实际问题。
在探索活动中,理解组合图形面积计算的多种方法,会找出计算每个简单图形所需的条件。
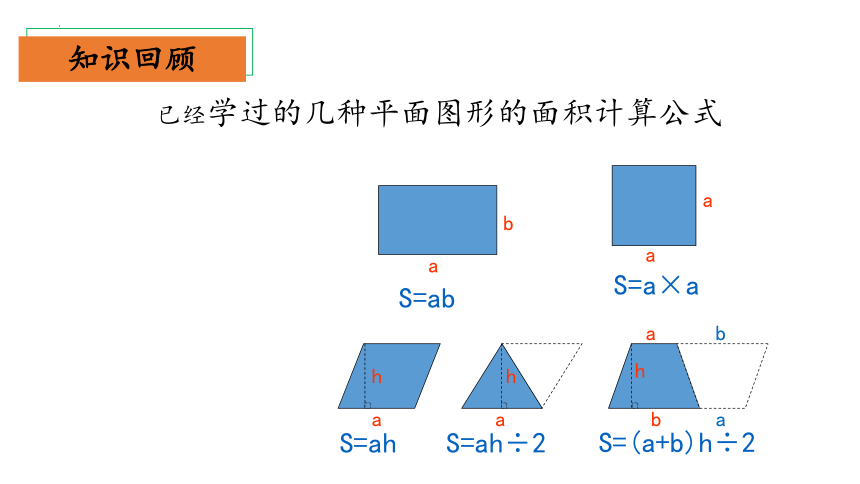
已经学过的几种平面图形的面积计算公式
a
b
a
a
h
a
h
a
a
b
h
a
b
S=ab
S=a×a
S=ah
S=ah÷2
S=(a+b)h÷2
同学们,老师准备了几幅漂亮的图片,我们一起来欣赏一下,好吗?
请大家仔细观察,这些物品的表面有哪些我们已经学过的图形?它们有什么共同特点呢?上面这些图形都是由几个简单图形组合而成的,这样的图形叫组合图形。
我们身边的组合图形
探究一
午间休息老师带同学们到儿童游乐场去游玩。这个游乐场的面积有多大呢?
探究一
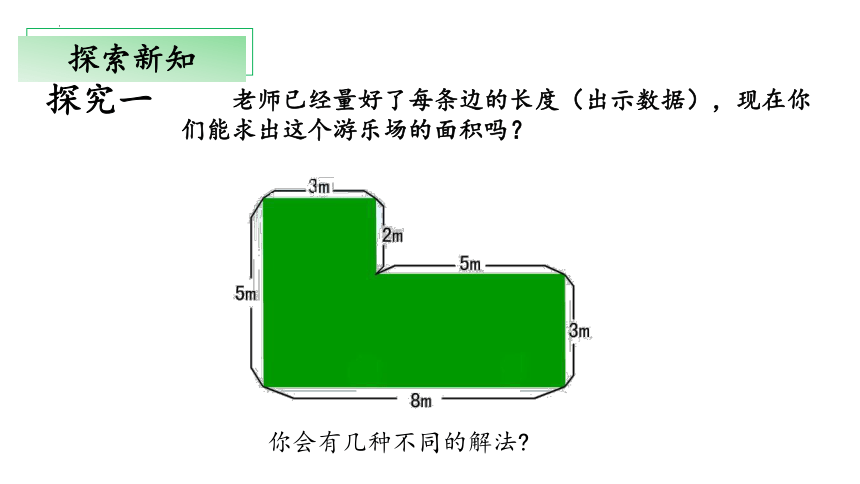
老师已经量好了每条边的长度(出示数据),现在你们能求出这个游乐场的面积吗?
你会有几种不同的解法
组合图形的面积
探究一
计算面积。
3×2+8×3
=6+24
=30(平方米)
探究一
3×5+5×3
=15+15
=30(平方米)
探究一
5×8-5×2
=40-10
=30(平方米)
探究一
3×2+8×3
=6+24
=30(平方米)
3×5+5×3
=15+15
=30(平方米)
5×8-5×2
=40-10
=30(平方米)
比较一下,这些方法中有什么共同的地方?
在计算不规则图形的面积时,可以采用割补法。通过分割成两个基本图形再求出面积或者补成一个基本图形再求出面积。
4m
9m
7m
7m
你会计算它的面积吗?
9×4+(9-7)×(7-4)
=36+6
=42(㎡)
7×4+(9-7)×7
=28+14
=42(㎡)
7×9-(7-4)×7
=63-21
=42(㎡)
2m
3m
10cm
5cm
5cm
5cm
(2)
(3)
说一说,下列组合图形面积你会如何计算?
5cm
5cm
10cm
9cm
4cm
4cm
6cm
12cm
8cm
4cm
4cm
8cm
4cm
4cm
(4)
(5)
说一说,下列组合图形面积你会如何计算?
8cm
4cm
4cm
8cm
4cm
4cm
(5)
说一说,下列组合图形面积你会如何计算?
8cm
4cm
4cm
8cm
4cm
4cm
小结:
计算组合图形的面积,一般是把它们分割或添补成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积之和或差。
试一试
20×10=200(dm2)
5×5=25(dm2)
200-25=175(m2)
20×10-5×5
=200-25
=175(dm2)
答:涂油漆部分的面积是175dm2。
8
20
15
18
单位:cm
解法一:
分解成一个长方形和一个梯形
解:由长方形面积公式
S长=a×b
=15×8
=120(cm2)
由梯形面积公式
S梯=(a+b) ×h÷2
=(8+18) ×(20-15) ÷2
=65(cm2)
S= S长+S梯=120+65=185(cm2)
8
20
15
18
单位:cm
解法二:
分解成一个长方形和一个三角形
解:由长方形面积公式
S长=ab
=20×8
=160(cm2)
由三角形面积公式
S三角形=ah ÷2
因为
a=18-8=10(cm)
h=20-15=5(cm)
所以
S三角形=ah ÷2
=10×5÷2
=25(cm2)
S=S长+S三角形
=160+25
=185(cm2)
还有没有其它方法吗?
8
20
15
18
8
20
15
18
一个长方形和一个梯形
一个三角形和一个梯形
计算下面图形的面积
分组讨论怎样计算
方法一:
左图分割成两个长方形
S1=4×(6-3)=12(cm2)
S2=3×7=21(cm2)
S=S1+S2=12+21=33(cm2)
4cm
6cm
7cm
3cm
方法二:
左图分割成一个长方形和一个正方形
S长方形=4×6=24(cm2)
S正方形=3×(7-4)=9( cm2 )
S=24+9=33(cm2)
7cm
4cm
3cm
6cm
同学们还有什么方法吗?
6cm
6cm
7cm
7cm
4cm
4cm
3cm
3cm
作业:
来自小红的求助信: 你能帮我算出少先队中队旗的面积吗?
Thank you!
组合图形的面积
小学数学·三年级(下)
沪教版·第一单元
明确组合图形的意义,掌握用分解法或添补法求组合图形的面积。
能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
渗透转化的教学思想,提高学生运用新知识解决实际问题的能力,在自主探索活动中培养创新精神。
重
择有效的计算方法解决实际问题。
在探索活动中,理解组合图形面积计算的多种方法,会找出计算每个简单图形所需的条件。
已经学过的几种平面图形的面积计算公式
a
b
a
a
h
a
h
a
a
b
h
a
b
S=ab
S=a×a
S=ah
S=ah÷2
S=(a+b)h÷2
同学们,老师准备了几幅漂亮的图片,我们一起来欣赏一下,好吗?
请大家仔细观察,这些物品的表面有哪些我们已经学过的图形?它们有什么共同特点呢?上面这些图形都是由几个简单图形组合而成的,这样的图形叫组合图形。
我们身边的组合图形
探究一
午间休息老师带同学们到儿童游乐场去游玩。这个游乐场的面积有多大呢?
探究一
老师已经量好了每条边的长度(出示数据),现在你们能求出这个游乐场的面积吗?
你会有几种不同的解法
组合图形的面积
探究一
计算面积。
3×2+8×3
=6+24
=30(平方米)
探究一
3×5+5×3
=15+15
=30(平方米)
探究一
5×8-5×2
=40-10
=30(平方米)
探究一
3×2+8×3
=6+24
=30(平方米)
3×5+5×3
=15+15
=30(平方米)
5×8-5×2
=40-10
=30(平方米)
比较一下,这些方法中有什么共同的地方?
在计算不规则图形的面积时,可以采用割补法。通过分割成两个基本图形再求出面积或者补成一个基本图形再求出面积。
4m
9m
7m
7m
你会计算它的面积吗?
9×4+(9-7)×(7-4)
=36+6
=42(㎡)
7×4+(9-7)×7
=28+14
=42(㎡)
7×9-(7-4)×7
=63-21
=42(㎡)
2m
3m
10cm
5cm
5cm
5cm
(2)
(3)
说一说,下列组合图形面积你会如何计算?
5cm
5cm
10cm
9cm
4cm
4cm
6cm
12cm
8cm
4cm
4cm
8cm
4cm
4cm
(4)
(5)
说一说,下列组合图形面积你会如何计算?
8cm
4cm
4cm
8cm
4cm
4cm
(5)
说一说,下列组合图形面积你会如何计算?
8cm
4cm
4cm
8cm
4cm
4cm
小结:
计算组合图形的面积,一般是把它们分割或添补成基本图形,如长方形、正方形、三角形、梯形等,再计算它们的面积之和或差。
试一试
20×10=200(dm2)
5×5=25(dm2)
200-25=175(m2)
20×10-5×5
=200-25
=175(dm2)
答:涂油漆部分的面积是175dm2。
8
20
15
18
单位:cm
解法一:
分解成一个长方形和一个梯形
解:由长方形面积公式
S长=a×b
=15×8
=120(cm2)
由梯形面积公式
S梯=(a+b) ×h÷2
=(8+18) ×(20-15) ÷2
=65(cm2)
S= S长+S梯=120+65=185(cm2)
8
20
15
18
单位:cm
解法二:
分解成一个长方形和一个三角形
解:由长方形面积公式
S长=ab
=20×8
=160(cm2)
由三角形面积公式
S三角形=ah ÷2
因为
a=18-8=10(cm)
h=20-15=5(cm)
所以
S三角形=ah ÷2
=10×5÷2
=25(cm2)
S=S长+S三角形
=160+25
=185(cm2)
还有没有其它方法吗?
8
20
15
18
8
20
15
18
一个长方形和一个梯形
一个三角形和一个梯形
计算下面图形的面积
分组讨论怎样计算
方法一:
左图分割成两个长方形
S1=4×(6-3)=12(cm2)
S2=3×7=21(cm2)
S=S1+S2=12+21=33(cm2)
4cm
6cm
7cm
3cm
方法二:
左图分割成一个长方形和一个正方形
S长方形=4×6=24(cm2)
S正方形=3×(7-4)=9( cm2 )
S=24+9=33(cm2)
7cm
4cm
3cm
6cm
同学们还有什么方法吗?
6cm
6cm
7cm
7cm
4cm
4cm
3cm
3cm
作业:
来自小红的求助信: 你能帮我算出少先队中队旗的面积吗?
Thank you!
