第十九章《一次函数》单元复习与检测(含答案)
文档属性
| 名称 | 第十九章《一次函数》单元复习与检测(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十九章《一次函数》单元复习与检测(含解答)
选择题(本大题共有10个小题,每小题3分,共30分)
1.一个正比例函数的图象经过点,它的表达式为( )
A. B. C. D.
2.将直线向上平移2个单位长度,得到的直线为( )
A. B. C. D.
已知一次函数y=(1+2m)x﹣3中,函数值y随自变量x的增大而减小,
那么m的取值范围是( )
A.m≤﹣ B.m≥﹣ C.m<﹣ D.m>
4.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
5.一次函数的图像与y轴交点的坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
点,,在一次函数(m是常数)的图象上,
则的大小关系是( )
A. B.
C. D.
7.关于一次函数,下列说法正确的是( )
A.图象经过点 B.图象与轴交于点
C.图象不经过第二象限 D.函数值随的增大而增大
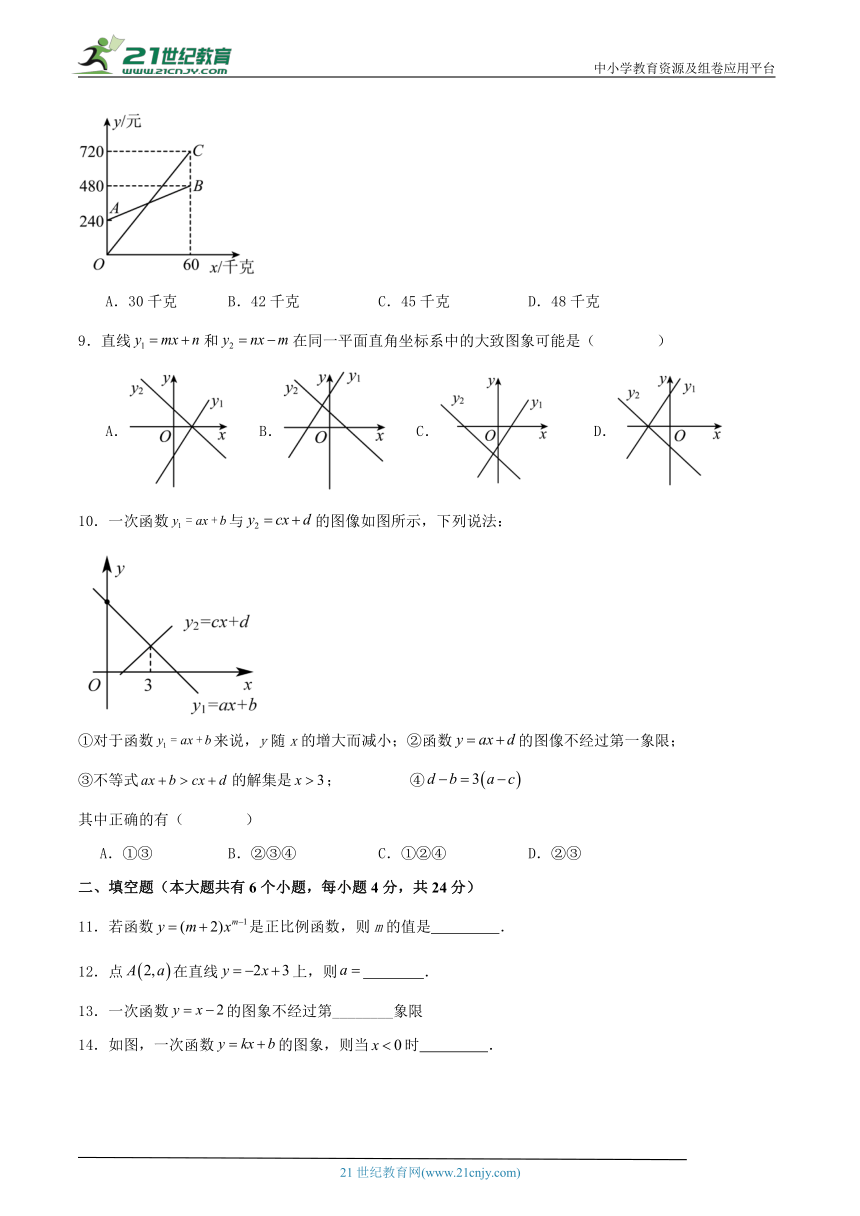
某网红店生产并销售一种特色食品,每天均能限量生产并销售完毕,
如图中的线段,分别表示某天生产成本(单位:元),
收入(单位:元)与产量x(单位:千克)之间的函数关系.根据图象信息可知,
该网红店某一天中盈利120元时的产量是( )
A.30千克 B.42千克 C.45千克 D.48千克
9.直线和在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
10.一次函数与的图像如图所示,下列说法:
①对于函数来说,y随x的增大而减小;②函数的图像不经过第一象限;
③不等式的解集是; ④
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
填空题(本大题共有6个小题,每小题4分,共24分)
11.若函数是正比例函数,则m的值是 .
12.点在直线上,则 .
13.一次函数的图象不经过第________象限
14.如图,一次函数的图象,则当时 .
15如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
则关于x的方程3x+b=ax﹣2的解为x= .
学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,
两人各自从家同时同向出发,沿同一条路匀速前进.
如图所示,和分别表示两人到小亮家的距离和时间的关系,
则出发 后两人相距.
三、解答题(本大题共有6个小题,共46分)
17.已知y是的正比例函数,且当时,.
(1)求y与x的函数关系式.
(2)若点在该函数的图象上,求a的值.
18.如图所示,直线是一次函数的图象.
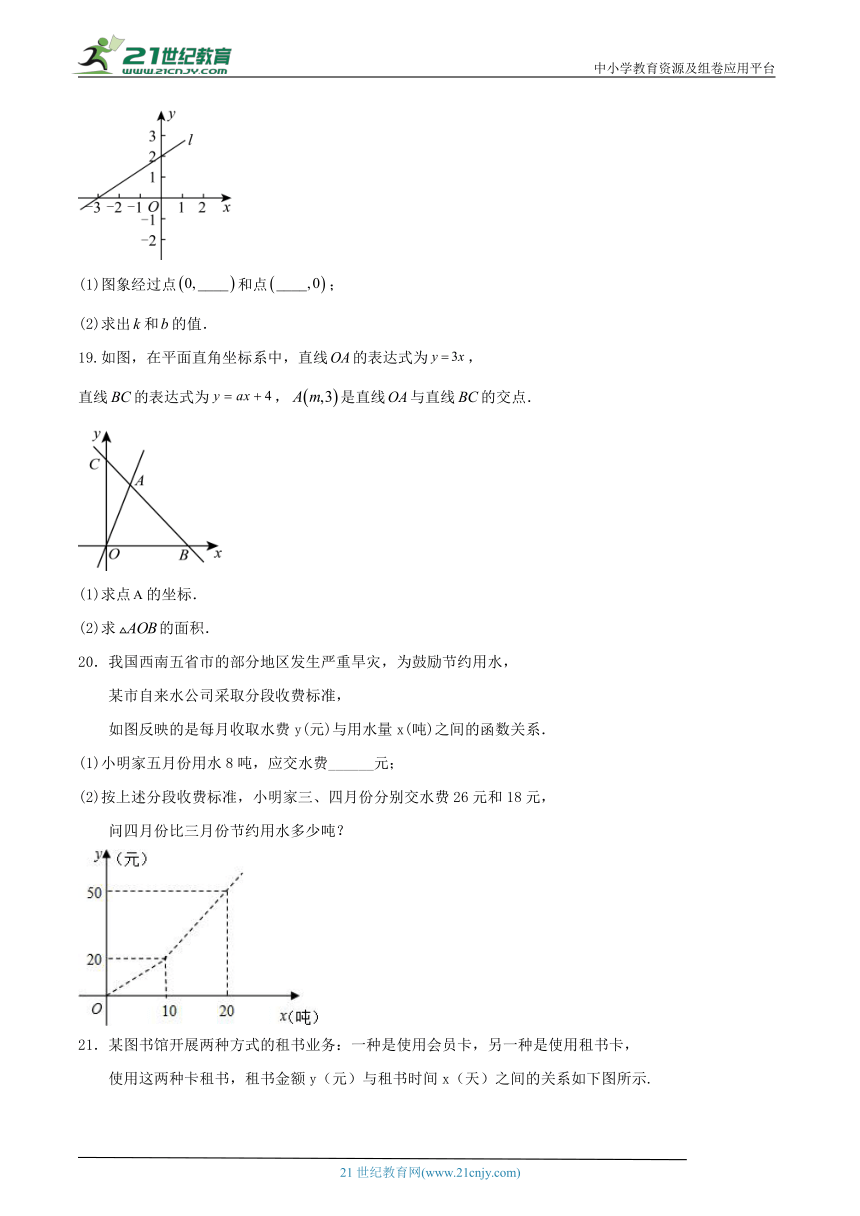
(1)图象经过点和点;
(2)求出和的值.
19.如图,在平面直角坐标系中,直线的表达式为,
直线的表达式为,是直线与直线的交点.
(1)求点的坐标.
(2)求的面积.
我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,
某市自来水公司采取分段收费标准,
如图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,
问四月份比三月份节约用水多少吨?
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,
使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下图所示.
(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式.
(2)两种租书方式每天的收费是多少元?(x<100)
如图,一次函数的图象与轴和轴分别交于点和点,
直线是直线的垂直平分线,直线与轴交于点,与交于点.
(1)点的坐标为________,点的坐标为________;
(2)的长________;
(3)设是x负半轴上一动点,若使是等腰三角形,则点的坐标为________.
第十九章《一次函数》单元复习与检测 解答
选择题(本大题共有10个小题,每小题3分,共30分)
1.一个正比例函数的图象经过点,它的表达式为( )
A. B. C. D.
【答案】A
2.将直线向上平移2个单位长度,得到的直线为( )
A. B. C. D.
【答案】D
已知一次函数y=(1+2m)x﹣3中,函数值y随自变量x的增大而减小,
那么m的取值范围是( )
A.m≤﹣ B.m≥﹣ C.m<﹣ D.m>
【答案】C
4.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
【答案】D
5.一次函数的图像与y轴交点的坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
【答案】B
6 .点,,在一次函数(m是常数)的图象上,
则的大小关系是( )
A. B.
C. D.
【答案】A
7.关于一次函数,下列说法正确的是( )
A.图象经过点 B.图象与轴交于点
C.图象不经过第二象限 D.函数值随的增大而增大
【答案】B
8 .某网红店生产并销售一种特色食品,每天均能限量生产并销售完毕,
如图中的线段,分别表示某天生产成本(单位:元),
收入(单位:元)与产量x(单位:千克)之间的函数关系.根据图象信息可知,
该网红店某一天中盈利120元时的产量是( )
A.30千克 B.42千克 C.45千克 D.48千克
【答案】C
9.直线和在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
【答案】C
10.一次函数与的图像如图所示,下列说法:
①对于函数来说,y随x的增大而减小;②函数的图像不经过第一象限;
③不等式的解集是; ④
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【答案】B
填空题(本大题共有6个小题,每小题4分,共24分)
11.若函数是正比例函数,则m的值是 .
【答案】
12.点在直线上,则 .
【答案】-1
13.一次函数的图象不经过第________象限
【答案】二
14.如图,一次函数的图象,则当时 .
【答案】
15如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
则关于x的方程3x+b=ax﹣2的解为x= .
【答案】﹣2
16.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,
两人各自从家同时同向出发,沿同一条路匀速前进.
如图所示,和分别表示两人到小亮家的距离和时间的关系,
则出发 后两人相距.
【答案】
三、解答题(本大题共有6个小题,共46分)
17.已知y是的正比例函数,且当时,.
(1)求y与x的函数关系式.
(2)若点在该函数的图象上,求a的值.
解:(1)设.
∵当时,,
∴,
∴,
∴.
(2)∵点在的图象上,
∴.
∴.
18.如图所示,直线是一次函数的图象.
(1)图象经过点和点;
(2)求出和的值.
解:(1)由图可知,图象经过点和点,
故答案为:2,;
(2)把点和点,代入得:
,
把①代入②,得,
∴,.
19.如图,在平面直角坐标系中,直线的表达式为,
直线的表达式为,是直线与直线的交点.
(1)求点的坐标.
(2)求的面积.
解:(1)因为直线过点,
所以,
所以,
所以.
(2)因为直线经过点,
所以,
解得:,
所以直线的表达式为,
令,,解得,
所以点的坐标为,
所以的面积.
20 .我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,
某市自来水公司采取分段收费标准,
如图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,
问四月份比三月份节约用水多少吨?
解:(1)根据图象可知,10吨以内每吨水应缴20÷10=2元,所以8×2=16(元),
故答案为16;
(2)由图可得10吨内每吨2元,当y=18时,知x<10,
∴x=18×=9,
当x 10时,可设y与x的关系为:y=kx+b,
由图可知,当x=10时,y=20,x=20时y=50,可解得k=3,b= 10,
∴y与x之间的函数关系式为:y=3x 10,
∴当y=26时,知x>10,有26=3x 10,解得x=12,
∴四月份比三月份节约用水:12 9=3(吨).
21 .某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,
使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下图所示.
(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式.
(2)两种租书方式每天的收费是多少元?(x<100)
解:(1)观察图象可知,用租书卡设其函数关系式为y=kx,
∵函数图象经过点(0,0)和(100,50),
∴50=k 100,
解得k=,即:函数关系式为y=x;
用会员卡租书可设其函数关系式为y=ax+b,
∵图象经过点(0,20)和(100,50),
∴ ,
解得:
即:函数关系式为y=x+20;
(2)用租书卡的方式租书,每天租书的收费为50÷100=0.5元;
用会员卡的方式租书,每天租书的收费为(50-20)÷100=0.3元.
22 .如图,一次函数的图象与轴和轴分别交于点和点,
直线是直线的垂直平分线,直线与轴交于点,与交于点.
(1)点的坐标为________,点的坐标为________;
(2)的长________;
(3)设是x负半轴上一动点,若使是等腰三角形,则点的坐标为________.
解:(1)在中,
当时,,
当时,,
∴,,
故答案为:,;
(2)∵,,
∴,
设,则,
∵直线是直线的垂直平分线,
∴,
在中,
由勾股定理得,
∴,
∴,
∴,
故答案为:;
(3)设点P的坐标为,
∴,
当时,则,
解得(舍去);
当时,则,解得或(舍去),
∴;
当时,则,解得或(舍去),
∴;
综上所述,点的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第十九章《一次函数》单元复习与检测(含解答)
选择题(本大题共有10个小题,每小题3分,共30分)
1.一个正比例函数的图象经过点,它的表达式为( )
A. B. C. D.
2.将直线向上平移2个单位长度,得到的直线为( )
A. B. C. D.
已知一次函数y=(1+2m)x﹣3中,函数值y随自变量x的增大而减小,
那么m的取值范围是( )
A.m≤﹣ B.m≥﹣ C.m<﹣ D.m>
4.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
5.一次函数的图像与y轴交点的坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
点,,在一次函数(m是常数)的图象上,
则的大小关系是( )
A. B.
C. D.
7.关于一次函数,下列说法正确的是( )
A.图象经过点 B.图象与轴交于点
C.图象不经过第二象限 D.函数值随的增大而增大
某网红店生产并销售一种特色食品,每天均能限量生产并销售完毕,
如图中的线段,分别表示某天生产成本(单位:元),
收入(单位:元)与产量x(单位:千克)之间的函数关系.根据图象信息可知,
该网红店某一天中盈利120元时的产量是( )
A.30千克 B.42千克 C.45千克 D.48千克
9.直线和在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
10.一次函数与的图像如图所示,下列说法:
①对于函数来说,y随x的增大而减小;②函数的图像不经过第一象限;
③不等式的解集是; ④
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
填空题(本大题共有6个小题,每小题4分,共24分)
11.若函数是正比例函数,则m的值是 .
12.点在直线上,则 .
13.一次函数的图象不经过第________象限
14.如图,一次函数的图象,则当时 .
15如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
则关于x的方程3x+b=ax﹣2的解为x= .
学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,
两人各自从家同时同向出发,沿同一条路匀速前进.
如图所示,和分别表示两人到小亮家的距离和时间的关系,
则出发 后两人相距.
三、解答题(本大题共有6个小题,共46分)
17.已知y是的正比例函数,且当时,.
(1)求y与x的函数关系式.
(2)若点在该函数的图象上,求a的值.
18.如图所示,直线是一次函数的图象.
(1)图象经过点和点;
(2)求出和的值.
19.如图,在平面直角坐标系中,直线的表达式为,
直线的表达式为,是直线与直线的交点.
(1)求点的坐标.
(2)求的面积.
我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,
某市自来水公司采取分段收费标准,
如图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,
问四月份比三月份节约用水多少吨?
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,
使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下图所示.
(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式.
(2)两种租书方式每天的收费是多少元?(x<100)
如图,一次函数的图象与轴和轴分别交于点和点,
直线是直线的垂直平分线,直线与轴交于点,与交于点.
(1)点的坐标为________,点的坐标为________;
(2)的长________;
(3)设是x负半轴上一动点,若使是等腰三角形,则点的坐标为________.
第十九章《一次函数》单元复习与检测 解答
选择题(本大题共有10个小题,每小题3分,共30分)
1.一个正比例函数的图象经过点,它的表达式为( )
A. B. C. D.
【答案】A
2.将直线向上平移2个单位长度,得到的直线为( )
A. B. C. D.
【答案】D
已知一次函数y=(1+2m)x﹣3中,函数值y随自变量x的增大而减小,
那么m的取值范围是( )
A.m≤﹣ B.m≥﹣ C.m<﹣ D.m>
【答案】C
4.直线y=kx+b经过一、二、四象限,则k、b应满足( )
A.k>0,b<0 B.k>0,b>0 C.k<0,b<0 D.k<0,b>0
【答案】D
5.一次函数的图像与y轴交点的坐标是( )
A.(0,-4) B.(0,4) C.(2,0) D.(-2,0)
【答案】B
6 .点,,在一次函数(m是常数)的图象上,
则的大小关系是( )
A. B.
C. D.
【答案】A
7.关于一次函数,下列说法正确的是( )
A.图象经过点 B.图象与轴交于点
C.图象不经过第二象限 D.函数值随的增大而增大
【答案】B
8 .某网红店生产并销售一种特色食品,每天均能限量生产并销售完毕,
如图中的线段,分别表示某天生产成本(单位:元),
收入(单位:元)与产量x(单位:千克)之间的函数关系.根据图象信息可知,
该网红店某一天中盈利120元时的产量是( )
A.30千克 B.42千克 C.45千克 D.48千克
【答案】C
9.直线和在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
【答案】C
10.一次函数与的图像如图所示,下列说法:
①对于函数来说,y随x的增大而减小;②函数的图像不经过第一象限;
③不等式的解集是; ④
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【答案】B
填空题(本大题共有6个小题,每小题4分,共24分)
11.若函数是正比例函数,则m的值是 .
【答案】
12.点在直线上,则 .
【答案】-1
13.一次函数的图象不经过第________象限
【答案】二
14.如图,一次函数的图象,则当时 .
【答案】
15如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,
则关于x的方程3x+b=ax﹣2的解为x= .
【答案】﹣2
16.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,
两人各自从家同时同向出发,沿同一条路匀速前进.
如图所示,和分别表示两人到小亮家的距离和时间的关系,
则出发 后两人相距.
【答案】
三、解答题(本大题共有6个小题,共46分)
17.已知y是的正比例函数,且当时,.
(1)求y与x的函数关系式.
(2)若点在该函数的图象上,求a的值.
解:(1)设.
∵当时,,
∴,
∴,
∴.
(2)∵点在的图象上,
∴.
∴.
18.如图所示,直线是一次函数的图象.
(1)图象经过点和点;
(2)求出和的值.
解:(1)由图可知,图象经过点和点,
故答案为:2,;
(2)把点和点,代入得:
,
把①代入②,得,
∴,.
19.如图,在平面直角坐标系中,直线的表达式为,
直线的表达式为,是直线与直线的交点.
(1)求点的坐标.
(2)求的面积.
解:(1)因为直线过点,
所以,
所以,
所以.
(2)因为直线经过点,
所以,
解得:,
所以直线的表达式为,
令,,解得,
所以点的坐标为,
所以的面积.
20 .我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,
某市自来水公司采取分段收费标准,
如图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.
(1)小明家五月份用水8吨,应交水费______元;
(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,
问四月份比三月份节约用水多少吨?
解:(1)根据图象可知,10吨以内每吨水应缴20÷10=2元,所以8×2=16(元),
故答案为16;
(2)由图可得10吨内每吨2元,当y=18时,知x<10,
∴x=18×=9,
当x 10时,可设y与x的关系为:y=kx+b,
由图可知,当x=10时,y=20,x=20时y=50,可解得k=3,b= 10,
∴y与x之间的函数关系式为:y=3x 10,
∴当y=26时,知x>10,有26=3x 10,解得x=12,
∴四月份比三月份节约用水:12 9=3(吨).
21 .某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,
使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如下图所示.
(1)分别写出用租书卡和会员卡租书金额y(元)与租书时间x(天)之间的关系式.
(2)两种租书方式每天的收费是多少元?(x<100)
解:(1)观察图象可知,用租书卡设其函数关系式为y=kx,
∵函数图象经过点(0,0)和(100,50),
∴50=k 100,
解得k=,即:函数关系式为y=x;
用会员卡租书可设其函数关系式为y=ax+b,
∵图象经过点(0,20)和(100,50),
∴ ,
解得:
即:函数关系式为y=x+20;
(2)用租书卡的方式租书,每天租书的收费为50÷100=0.5元;
用会员卡的方式租书,每天租书的收费为(50-20)÷100=0.3元.
22 .如图,一次函数的图象与轴和轴分别交于点和点,
直线是直线的垂直平分线,直线与轴交于点,与交于点.
(1)点的坐标为________,点的坐标为________;
(2)的长________;
(3)设是x负半轴上一动点,若使是等腰三角形,则点的坐标为________.
解:(1)在中,
当时,,
当时,,
∴,,
故答案为:,;
(2)∵,,
∴,
设,则,
∵直线是直线的垂直平分线,
∴,
在中,
由勾股定理得,
∴,
∴,
∴,
故答案为:;
(3)设点P的坐标为,
∴,
当时,则,
解得(舍去);
当时,则,解得或(舍去),
∴;
当时,则,解得或(舍去),
∴;
综上所述,点的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
