沪教版(五四学制)九年级数学下册学案:27.3正多边形与圆(无答案)
文档属性
| 名称 | 沪教版(五四学制)九年级数学下册学案:27.3正多边形与圆(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-06 08:52:22 | ||
图片预览



文档简介
课 题 正多边形与圆
教学目标 1.了解正多边形和圆的有关概念及对称性;2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;3.会进行正多边形的有关计算.
重点、难点 正多边形半径和边长、边心距、中心角之间的关系
考点及考试要求 会进行正多边形的有关计算
教学内容
一【要点梳理】知识点一、正多边形的概念
各边相等, ( http: / / www.21cnjy.com )各角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
知识点二、正多边形的重要元素
1.正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
3.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
知识点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
( http: / / www.21cnjy.com )
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.5.任何正多边形都有一个外接圆和一个内切圆 ( http: / / www.21cnjy.com ),这两个圆是同心圆
要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.知识点四、正多边形的画法
1.用量角器等分圆
由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形.
2.用尺规等分圆
对于一些特殊的正n边形,可以用圆规和直尺作图.
①正四、八边形。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形。 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形。
②正六、三、十二边形的作法。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点。
显然,A、E、F(或C、B、D)是⊙O的3等分点。
同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分……。
要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.二【典型例题】类型一、正多边形的概念例1.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )A.45° B.60° C.75° D.90° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【答案】A.【解析】如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=∠BOC=45°.
故选A.【点评】本题主要考查了正方形的性质和圆周角定理的应用.
举一反三:【变式】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )A.30° B.45° C.55° D.60° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.
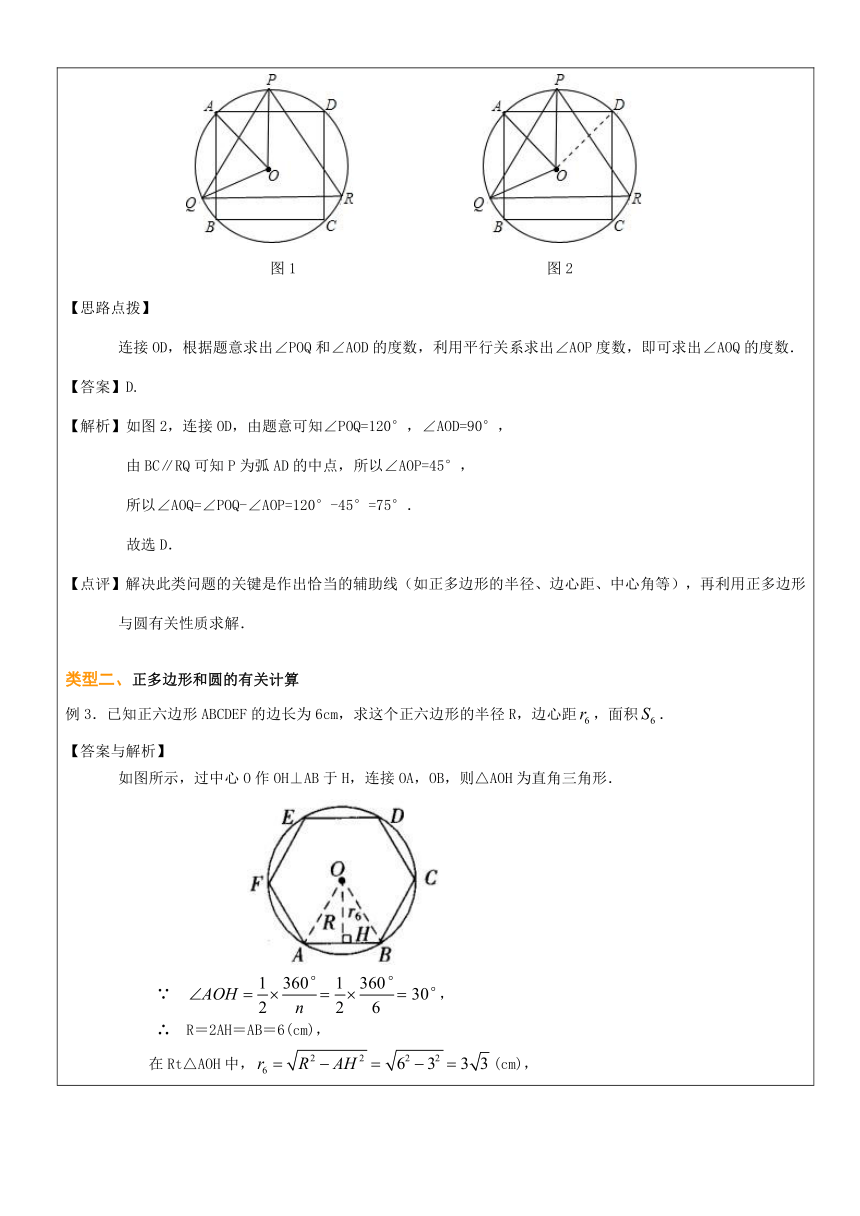
故选B.例2.如图1,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )A.60° B.65° C.72° D.75° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )图1 图2【思路点拨】 连接OD,根据题意求出∠POQ和∠AOD的度数,利用平行关系求出∠AOP度数,即可求出∠AOQ的度数.【答案】D.【解析】如图2,连接OD,由题意可知∠PO ( http: / / www.21cnjy.com )Q=120°,∠AOD=90°,
由BC∥RQ可知P为弧AD的中点,所以∠AOP=45°,
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°.
故选D.【点评】解决此类问题的关键是作出恰当的辅助线(如正多边形的半径、边心距、中心角等),再利用正多边形与圆有关性质求解.类型二、正多边形和圆的有关计算例3.已知正六边形ABCDEF的边长为6cm,求这个正六边形的半径R,边心距,面积.【答案与解析】 如图所示,过中心O作OH⊥AB于H,连接OA,OB,则△AOH为直角三角形. ( http: / / www.21cnjy.com )∵ ,∴ R=2AH=AB=6(cm),在Rt△AOH中,(cm),∴ (cm).【点评】关于正多边形与圆的计算问题一般转化为解由半径、边心距、边长的一半组成的直角三角形. 例4.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )A. B. C. D. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【思路点拨】 根据正多边形的特点,构建直角三角形来解决.【答案】B.【解析】连结OC1,作OF⊥C1D1于F,交BC于E.图形中正方形A1B1C1D1和正方形ABCD一定相似,OF,OC1分别等于两个正方形的边心距,△OC1F是等腰直角三角形,因而OF:OC1=,因而则的值为.故选B.【点评】边数相同的正多边形一定相似,边心距的比,半径的比都等于相似比.举一反三:【变式】如图是对称中心为点的正六边形.如果用一个含角的直角三角板的角,借助点(使角的顶点落在点处),把这个正六边形的面积等分,那么的所有可能的值是 ___________ __ . 【答案】根据圆内接正多边形的性质可 ( http: / / www.21cnjy.com )知,只要把此正六边形再化为正多边形即可,
即可知:360÷30=12;
360÷60=6;
360÷90=4;
360÷120=3;
360÷180=2.
故么n的所有可能的值是2,3,4,6,12.三【巩固练习】一、选择题
1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )A.9 B.8 C.7 D.62.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( ) A. cm B. cm C.cm D.1 cm ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )第2题图 第3题图 第5题图3.如图所示,两个正六边形的边长均为1 ( http: / / www.21cnjy.com ),其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是 ( )A.7 B.8 C.9 D.104.正三角形、正方形、圆三者的周长都等于,它们的面积分别为S1,S2、S3,则( ). A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S35.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).A.30° B.35° C.36° D.37° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 第6题图 第7题图 第9题图6.如图所示,是由5把相同的折扇组 ( http: / / www.21cnjy.com )成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )A.36° B.42° C.45° D.48°二、填空题7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠等于________.8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________.9.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径是________.10.正六边形的周长为12,则同半径的正三角形的面积为________,同半径的正方形的周长为________.11.正六边形的半径是5cm,则边长________,周长________ ,边心距________,面积________. 12. 正六边形的外接圆的半径与内切圆的半径之比为 .三、解答题13.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S. ( http: / / www.21cnjy.com )14. 如图所示,半径为R的圆绕周长为10πR的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈? ( http: / / www.21cnjy.com ) 一位同学的解答过程:圆的周长为2πR,所以它绕完正六边形后一共转了圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.15.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行了如下讨论:甲同学:这种多边形不一定是正多边形,如圆内接矩形.乙同学:我发现边数是6时,它也不一定是正多边形,如图①所示,△ABC是正三角形,,可以证明六边形ADBECF各内角相等,但它不是正六边形.丙同学:我能证明,边数是5时,它是正多边形,我想,边数是7时,它可能也是正多边形. ( http: / / www.21cnjy.com ) (1)请你证明乙同学构造的六边形各内角相等;(2)请你证明各内角相等的圆内接七边形ABCDEFG(如图②所示)是正七边形(不必写已知、求证).(3)根据以上探索过程,提出你的猜想(不必证明).
教学目标 1.了解正多边形和圆的有关概念及对称性;2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;3.会进行正多边形的有关计算.
重点、难点 正多边形半径和边长、边心距、中心角之间的关系
考点及考试要求 会进行正多边形的有关计算
教学内容
一【要点梳理】知识点一、正多边形的概念
各边相等, ( http: / / www.21cnjy.com )各角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
知识点二、正多边形的重要元素
1.正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
3.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
知识点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
( http: / / www.21cnjy.com )
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.5.任何正多边形都有一个外接圆和一个内切圆 ( http: / / www.21cnjy.com ),这两个圆是同心圆
要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.知识点四、正多边形的画法
1.用量角器等分圆
由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形.
2.用尺规等分圆
对于一些特殊的正n边形,可以用圆规和直尺作图.
①正四、八边形。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形。 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形。
②正六、三、十二边形的作法。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点。
显然,A、E、F(或C、B、D)是⊙O的3等分点。
同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分……。
要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.二【典型例题】类型一、正多边形的概念例1.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )A.45° B.60° C.75° D.90° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【答案】A.【解析】如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=∠BOC=45°.
故选A.【点评】本题主要考查了正方形的性质和圆周角定理的应用.
举一反三:【变式】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )A.30° B.45° C.55° D.60° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.
故选B.例2.如图1,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )A.60° B.65° C.72° D.75° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )图1 图2【思路点拨】 连接OD,根据题意求出∠POQ和∠AOD的度数,利用平行关系求出∠AOP度数,即可求出∠AOQ的度数.【答案】D.【解析】如图2,连接OD,由题意可知∠PO ( http: / / www.21cnjy.com )Q=120°,∠AOD=90°,
由BC∥RQ可知P为弧AD的中点,所以∠AOP=45°,
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°.
故选D.【点评】解决此类问题的关键是作出恰当的辅助线(如正多边形的半径、边心距、中心角等),再利用正多边形与圆有关性质求解.类型二、正多边形和圆的有关计算例3.已知正六边形ABCDEF的边长为6cm,求这个正六边形的半径R,边心距,面积.【答案与解析】 如图所示,过中心O作OH⊥AB于H,连接OA,OB,则△AOH为直角三角形. ( http: / / www.21cnjy.com )∵ ,∴ R=2AH=AB=6(cm),在Rt△AOH中,(cm),∴ (cm).【点评】关于正多边形与圆的计算问题一般转化为解由半径、边心距、边长的一半组成的直角三角形. 例4.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )A. B. C. D. ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )【思路点拨】 根据正多边形的特点,构建直角三角形来解决.【答案】B.【解析】连结OC1,作OF⊥C1D1于F,交BC于E.图形中正方形A1B1C1D1和正方形ABCD一定相似,OF,OC1分别等于两个正方形的边心距,△OC1F是等腰直角三角形,因而OF:OC1=,因而则的值为.故选B.【点评】边数相同的正多边形一定相似,边心距的比,半径的比都等于相似比.举一反三:【变式】如图是对称中心为点的正六边形.如果用一个含角的直角三角板的角,借助点(使角的顶点落在点处),把这个正六边形的面积等分,那么的所有可能的值是 ___________ __ . 【答案】根据圆内接正多边形的性质可 ( http: / / www.21cnjy.com )知,只要把此正六边形再化为正多边形即可,
即可知:360÷30=12;
360÷60=6;
360÷90=4;
360÷120=3;
360÷180=2.
故么n的所有可能的值是2,3,4,6,12.三【巩固练习】一、选择题
1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )A.9 B.8 C.7 D.62.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是( ) A. cm B. cm C.cm D.1 cm ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )第2题图 第3题图 第5题图3.如图所示,两个正六边形的边长均为1 ( http: / / www.21cnjy.com ),其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是 ( )A.7 B.8 C.9 D.104.正三角形、正方形、圆三者的周长都等于,它们的面积分别为S1,S2、S3,则( ). A.S1=S2=S3 B.S3<S1<S2 C.S1<S2<S3 D.S2<S1<S35.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是( ).A.30° B.35° C.36° D.37° ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) 第6题图 第7题图 第9题图6.如图所示,是由5把相同的折扇组 ( http: / / www.21cnjy.com )成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )A.36° B.42° C.45° D.48°二、填空题7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠等于________.8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________.9.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径是________.10.正六边形的周长为12,则同半径的正三角形的面积为________,同半径的正方形的周长为________.11.正六边形的半径是5cm,则边长________,周长________ ,边心距________,面积________. 12. 正六边形的外接圆的半径与内切圆的半径之比为 .三、解答题13.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S. ( http: / / www.21cnjy.com )14. 如图所示,半径为R的圆绕周长为10πR的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈? ( http: / / www.21cnjy.com ) 一位同学的解答过程:圆的周长为2πR,所以它绕完正六边形后一共转了圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.15.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行了如下讨论:甲同学:这种多边形不一定是正多边形,如圆内接矩形.乙同学:我发现边数是6时,它也不一定是正多边形,如图①所示,△ABC是正三角形,,可以证明六边形ADBECF各内角相等,但它不是正六边形.丙同学:我能证明,边数是5时,它是正多边形,我想,边数是7时,它可能也是正多边形. ( http: / / www.21cnjy.com ) (1)请你证明乙同学构造的六边形各内角相等;(2)请你证明各内角相等的圆内接七边形ABCDEFG(如图②所示)是正七边形(不必写已知、求证).(3)根据以上探索过程,提出你的猜想(不必证明).
