2.2二次函数的图象与性质分类训练(无答案) 2023-—2024学年北师大版数学九年级下册
文档属性
| 名称 | 2.2二次函数的图象与性质分类训练(无答案) 2023-—2024学年北师大版数学九年级下册 | 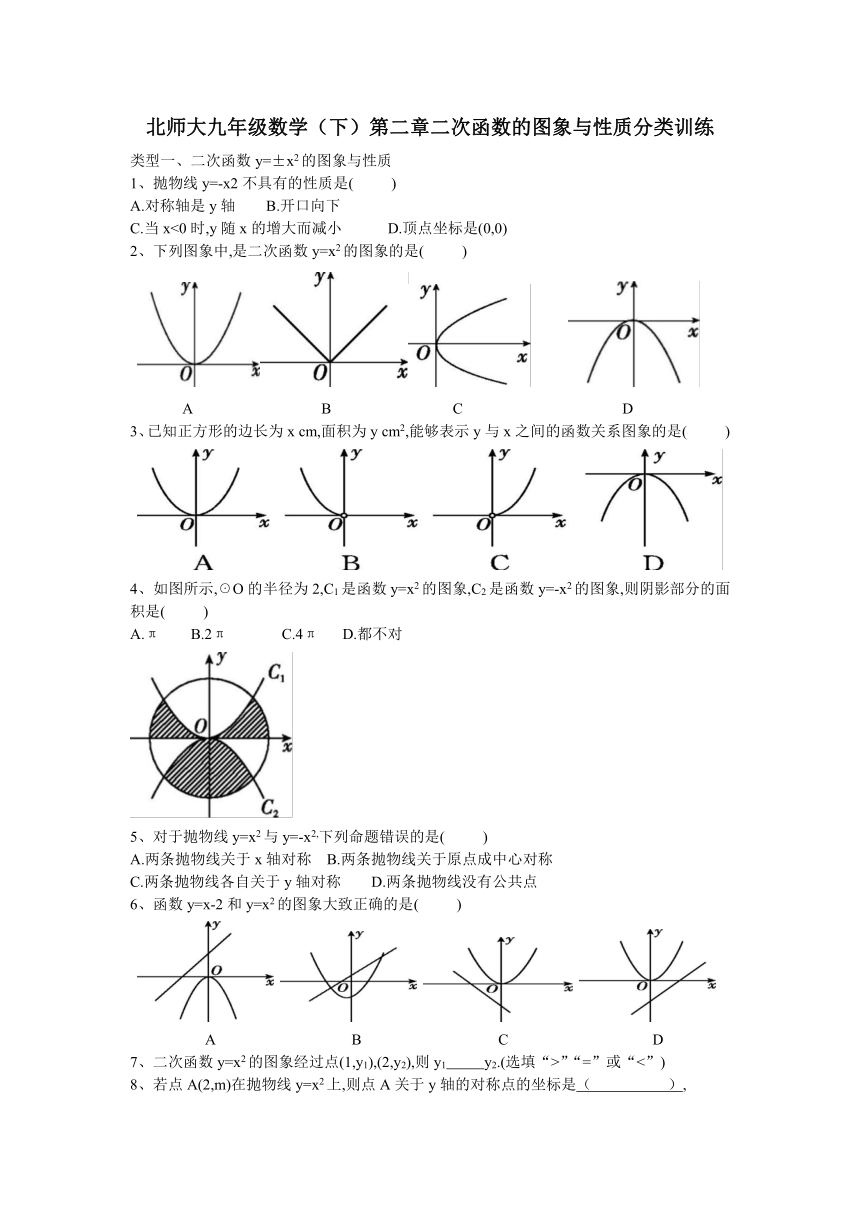 | |
| 格式 | docx | ||
| 文件大小 | 404.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 11:56:50 | ||
图片预览



文档简介
北师大九年级数学(下)第二章二次函数的图象与性质分类训练
类型一、二次函数y=±x2的图象与性质
1、抛物线y=-x2不具有的性质是( )
A.对称轴是y轴 B.开口向下
C.当x<0时,y随x的增大而减小 D.顶点坐标是(0,0)
2、下列图象中,是二次函数y=x2的图象的是( )
A B C D
3、已知正方形的边长为x cm,面积为y cm2,能够表示y与x之间的函数关系图象的是( )
4、如图所示,☉O的半径为2,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是( )
A.π B.2π C.4π D.都不对
5、对于抛物线y=x2与y=-x2,下列命题错误的是( )
A.两条抛物线关于x轴对称 B.两条抛物线关于原点成中心对称
C.两条抛物线各自关于y轴对称 D.两条抛物线没有公共点
6、函数y=x-2和y=x2的图象大致正确的是( )
A B C D
7、二次函数y=x2的图象经过点(1,y1),(2,y2),则y1 y2.(选填“>”“=”或“<”)
8、若点A(2,m)在抛物线y=x2上,则点A关于y轴的对称点的坐标是( ),
它 (填“在”或“不在”)抛物线y=x2上.
9、已知y=nxn2-2是关于x的二次函数,且有最大值,则n的值是 .
10、抛物线y=-x2上一点到x轴的距离是9,则该点的坐标是 .
11、已知点A(1,a)在抛物线y=x2上,求点A的坐标.
12、根据二次函数y=-x2的图象,回答下列问题:
(1)写出它的图象与x轴的交点坐标.
(2)当x取什么值时,y值最大 最大值是多少
(3)当1(4)当-313、已知函数y=ax2(a≠0)的图象与函数y=2x-3的图象交于点(1,b).
(1)试求a和b的值;
(2)求函数y=ax2的表达式,并求其图象的顶点坐标和对称轴;
(3)x取何值时,函数y=ax2中的y值随x值的增大而增大
14、如图所示,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
(1)求△AOP的面积S与y的关系式.
(2)S是y的什么函数 S是x的什么函数
15、已知A(1,1),B(3,9)是抛物线y=x2上的两点,在y轴上有一动点P,当△PAB的周长最小时,
试求点P的坐标.
类型二、二次函数y=ax2的图象与性质
16、下列说法中,错误的是( )
A.二次函数y=3x2的图象有最低点
B.二次函数y=-6x2,当x=0时,y有最大值0
C.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
D.二次项系数a越大,图象开口越小;a越小,图象开口越大
17、若二次函数y=ax2的图象经过点P(-3,9),则该图象必经过点( )
A.(3,9) B.(-3,-9) C.(-9,3) D.(9,-3)
18、已知m<-1,点(m-1,y1),(m,y2),(m+1,y3)都在二次函数y=x2的图象上,则( )
A.y119、二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
20、抛物线y=3x2与直线y=kx+2的交点为(2,b),则k+b= .
21、对于二次函数y=ax2,若当x由1增加到2时,函数值减少3,则常数a的值是 .
22、对于二次函数y=ax2和y=bx2,其自变量和函数值的两组对应值如下表所示.根据二次
函数的相关性质,可求出d-c= .
23、如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和点 B(3,0)
构成平行四边形ABCD,DC与y轴的交点为点E(0,6),则a的值为 .
24、根据条件,求下列各题中m的取值或取值范围.
(1)函数y=(2m-1)x2有最小值;
(2)函数y=(m-2)x2,当x<0时,y随着x的增大而增大;
(3)y=(m+1)x2与y=2x2的函数图象形状相同;
25、如图所示,已知y=-2x+3的图象与y=x2的图象交于A,B两点,且与x轴,y轴分别交于
D,C两点,O为坐标原点.
(1)求点A,B的坐标;
(2)求S△AOB.
类型三、二次函数y=ax2+k的图象与性质
26、抛物线y=2x2+4与y轴的交点坐标是( )
A.(0,2) B.(0,-2) C.(0,4) D.(0,-4)
27、二次函数y=-x2-2的图象大致是( )
28、将抛物线y=2x2平移后得到抛物线y=2x2+1,则平移方式为( )
A.向左平移1个单位 B.向右平移1个单位
C.向上平移1个单位 D.向下平移1个单位
29、已知抛物线y=-x2+1,下列结论:①抛物线开口向上;②抛物线与x轴交于点(-1,0)和点
(1,0)③抛物线的对称轴是y轴;④抛物线的顶点坐标是(0,1);⑤抛物线y=-x2+1是由抛物
线y=-x2向上平移1个单位得到的.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
31、如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是 。
32、如果二次函数y=(a+3)x2-5的图象不经过第一象限,那么a的取值范围是 。
33、已知二次函数y=x2-3的图象如图所示.
(1)作出二次函数y=x2-3图象关于x轴对称的图象;
(2)写出新抛物线的表达式;
(3)两个图象的顶点分别为C,D,与x轴的交点为A,B,试判断四边形ACBD的形状,并说明理由.
将函数y=ax2+4(a≠0)的图象沿y轴向下平移4个单位后,与直线y=kx-2相交于A,B
两点,其中点A的坐标是(-1,-1).
求a,k的值;
求点B的坐标.
类型四、二次函数y=a(x-h)2的图象与性质
35、把抛物线y=-3x2向右平移2个单位就是抛物线( )
A.y=-3x2+2 B.y=-3x2-2 C.y=-3(x+2)2 D.y=-3(x-2)2
36、在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是( )
A B C D
37、已知函数y=(x-1)2,下列结论正确的是( )
A.当x>0时,y随x的增大而减小
B.当x<0时,y随x的增大而增大
C.当x<1时,y随x的增大而减小
D.当x<-1时,y随x的增大而增大
38、已知抛物线y=(x-2)2上任意两点A(x1,y1)与B(x2,y2),若x2>x1>2,则y1和y2的大小关系是( )
A.y1>y2 B.y139、已知二次函数y=-(x-h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,则h的值为( )
A.3或6 B.1或6 C.1或3 D.4或6
40、在平面直角坐标系中,二次函数y=-(x-3)2的图象的顶点为A,与y轴交于点B.若在该二次函数图象上取一点C,在x轴上取一点D,使得四边形ABCD为平行四边形,则点D的坐标为( )
A.(-9,0) B.(-6,0) C.(6,0) D.(9,0)
41、如图所示,△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作 DE∥AC,交BC于点E,过点E作EF⊥DE,交AB的延长线于点F,设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
42、抛物线y=a(x-h)2与抛物线y=2x2的形状相同,但开口方向相反,对称轴与抛物线y=(x-2)2相同.
(1)求抛物线y=a(x-h)2的表达式;
(2)求抛物线y=a(x-h)2与y轴的交点坐标.
43、已知一条抛物线的开口方向和形状与y=3x2相同,顶点在抛物线y=(x+2)2的顶点上.
(1)求这条抛物线的表达式;
(2)求将(1)中的抛物线向右平移4个单位后得到的新抛物线的表达式;
(3)若(1)中的抛物线的顶点不变,开口方向相反,求所得的新抛物线的表达式.
44、如图所示,以点A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0),(0,4).
(1)求此抛物线的表达式;
(2)将y轴向右平移6个单位,写出此时抛物线的表达式;
(3)抛物线上是否存在一点P,使AB=AP 若存在,请求出点P的坐标;若不存在,请说明理由.
类型四、二次函数y=ax2+bx+c的图象与性质
45、抛物线y=-3x2+6x+2的对称轴是( )
A.直线x=2 B.直线x=-2 C.直线x=1 D.直线x=-1
46、将二次函数y=x2-2x-2化成y=a(x-h)2+k的形式为( )
A.y=(x-2)2-2 B.y=(x-1)2-3 C.y=(x-1)2-2 D.y=(x-2)2-3
47、将抛物线y=x2-6x+5向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
48、二次函数y=-2x2-4x+5的最大值是 .
49、若抛物线y=x2-bx+9的顶点在x轴负半轴上,则b的值为 .
50、已知二次函数y=x2+2mx+2,当x>2时,y的值随x的增大而增大,则实数m的取值范围是 .
51、设二次函数y=(ax-2)(x-2a),其中a是常数.
(1)当a=2时,试判断点(1,0)是否在该函数图象上;
(2)用含a的代数式表示函数图象的对称轴;
52、在平面直角坐标系xOy中,点(1,m)和点(3,n)在二次函数y=x2+bx的图象上.
(1)当m=-3时:
①求这个二次函数的顶点坐标;
②若点(-1,y1),(a,y2)在此二次函数的图象上,且y2>y1,则a的取值范围是多少?
(2)当mn<0时,求b的取值范围
类型一、二次函数y=±x2的图象与性质
1、抛物线y=-x2不具有的性质是( )
A.对称轴是y轴 B.开口向下
C.当x<0时,y随x的增大而减小 D.顶点坐标是(0,0)
2、下列图象中,是二次函数y=x2的图象的是( )
A B C D
3、已知正方形的边长为x cm,面积为y cm2,能够表示y与x之间的函数关系图象的是( )
4、如图所示,☉O的半径为2,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是( )
A.π B.2π C.4π D.都不对
5、对于抛物线y=x2与y=-x2,下列命题错误的是( )
A.两条抛物线关于x轴对称 B.两条抛物线关于原点成中心对称
C.两条抛物线各自关于y轴对称 D.两条抛物线没有公共点
6、函数y=x-2和y=x2的图象大致正确的是( )
A B C D
7、二次函数y=x2的图象经过点(1,y1),(2,y2),则y1 y2.(选填“>”“=”或“<”)
8、若点A(2,m)在抛物线y=x2上,则点A关于y轴的对称点的坐标是( ),
它 (填“在”或“不在”)抛物线y=x2上.
9、已知y=nxn2-2是关于x的二次函数,且有最大值,则n的值是 .
10、抛物线y=-x2上一点到x轴的距离是9,则该点的坐标是 .
11、已知点A(1,a)在抛物线y=x2上,求点A的坐标.
12、根据二次函数y=-x2的图象,回答下列问题:
(1)写出它的图象与x轴的交点坐标.
(2)当x取什么值时,y值最大 最大值是多少
(3)当1
(1)试求a和b的值;
(2)求函数y=ax2的表达式,并求其图象的顶点坐标和对称轴;
(3)x取何值时,函数y=ax2中的y值随x值的增大而增大
14、如图所示,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
(1)求△AOP的面积S与y的关系式.
(2)S是y的什么函数 S是x的什么函数
15、已知A(1,1),B(3,9)是抛物线y=x2上的两点,在y轴上有一动点P,当△PAB的周长最小时,
试求点P的坐标.
类型二、二次函数y=ax2的图象与性质
16、下列说法中,错误的是( )
A.二次函数y=3x2的图象有最低点
B.二次函数y=-6x2,当x=0时,y有最大值0
C.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
D.二次项系数a越大,图象开口越小;a越小,图象开口越大
17、若二次函数y=ax2的图象经过点P(-3,9),则该图象必经过点( )
A.(3,9) B.(-3,-9) C.(-9,3) D.(9,-3)
18、已知m<-1,点(m-1,y1),(m,y2),(m+1,y3)都在二次函数y=x2的图象上,则( )
A.y1
20、抛物线y=3x2与直线y=kx+2的交点为(2,b),则k+b= .
21、对于二次函数y=ax2,若当x由1增加到2时,函数值减少3,则常数a的值是 .
22、对于二次函数y=ax2和y=bx2,其自变量和函数值的两组对应值如下表所示.根据二次
函数的相关性质,可求出d-c= .
23、如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和点 B(3,0)
构成平行四边形ABCD,DC与y轴的交点为点E(0,6),则a的值为 .
24、根据条件,求下列各题中m的取值或取值范围.
(1)函数y=(2m-1)x2有最小值;
(2)函数y=(m-2)x2,当x<0时,y随着x的增大而增大;
(3)y=(m+1)x2与y=2x2的函数图象形状相同;
25、如图所示,已知y=-2x+3的图象与y=x2的图象交于A,B两点,且与x轴,y轴分别交于
D,C两点,O为坐标原点.
(1)求点A,B的坐标;
(2)求S△AOB.
类型三、二次函数y=ax2+k的图象与性质
26、抛物线y=2x2+4与y轴的交点坐标是( )
A.(0,2) B.(0,-2) C.(0,4) D.(0,-4)
27、二次函数y=-x2-2的图象大致是( )
28、将抛物线y=2x2平移后得到抛物线y=2x2+1,则平移方式为( )
A.向左平移1个单位 B.向右平移1个单位
C.向上平移1个单位 D.向下平移1个单位
29、已知抛物线y=-x2+1,下列结论:①抛物线开口向上;②抛物线与x轴交于点(-1,0)和点
(1,0)③抛物线的对称轴是y轴;④抛物线的顶点坐标是(0,1);⑤抛物线y=-x2+1是由抛物
线y=-x2向上平移1个单位得到的.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2
A.a>0 B.a<0 C.a≥0 D.a≤0
31、如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是 。
32、如果二次函数y=(a+3)x2-5的图象不经过第一象限,那么a的取值范围是 。
33、已知二次函数y=x2-3的图象如图所示.
(1)作出二次函数y=x2-3图象关于x轴对称的图象;
(2)写出新抛物线的表达式;
(3)两个图象的顶点分别为C,D,与x轴的交点为A,B,试判断四边形ACBD的形状,并说明理由.
将函数y=ax2+4(a≠0)的图象沿y轴向下平移4个单位后,与直线y=kx-2相交于A,B
两点,其中点A的坐标是(-1,-1).
求a,k的值;
求点B的坐标.
类型四、二次函数y=a(x-h)2的图象与性质
35、把抛物线y=-3x2向右平移2个单位就是抛物线( )
A.y=-3x2+2 B.y=-3x2-2 C.y=-3(x+2)2 D.y=-3(x-2)2
36、在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是( )
A B C D
37、已知函数y=(x-1)2,下列结论正确的是( )
A.当x>0时,y随x的增大而减小
B.当x<0时,y随x的增大而增大
C.当x<1时,y随x的增大而减小
D.当x<-1时,y随x的增大而增大
38、已知抛物线y=(x-2)2上任意两点A(x1,y1)与B(x2,y2),若x2>x1>2,则y1和y2的大小关系是( )
A.y1>y2 B.y1
A.3或6 B.1或6 C.1或3 D.4或6
40、在平面直角坐标系中,二次函数y=-(x-3)2的图象的顶点为A,与y轴交于点B.若在该二次函数图象上取一点C,在x轴上取一点D,使得四边形ABCD为平行四边形,则点D的坐标为( )
A.(-9,0) B.(-6,0) C.(6,0) D.(9,0)
41、如图所示,△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作 DE∥AC,交BC于点E,过点E作EF⊥DE,交AB的延长线于点F,设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
42、抛物线y=a(x-h)2与抛物线y=2x2的形状相同,但开口方向相反,对称轴与抛物线y=(x-2)2相同.
(1)求抛物线y=a(x-h)2的表达式;
(2)求抛物线y=a(x-h)2与y轴的交点坐标.
43、已知一条抛物线的开口方向和形状与y=3x2相同,顶点在抛物线y=(x+2)2的顶点上.
(1)求这条抛物线的表达式;
(2)求将(1)中的抛物线向右平移4个单位后得到的新抛物线的表达式;
(3)若(1)中的抛物线的顶点不变,开口方向相反,求所得的新抛物线的表达式.
44、如图所示,以点A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0),(0,4).
(1)求此抛物线的表达式;
(2)将y轴向右平移6个单位,写出此时抛物线的表达式;
(3)抛物线上是否存在一点P,使AB=AP 若存在,请求出点P的坐标;若不存在,请说明理由.
类型四、二次函数y=ax2+bx+c的图象与性质
45、抛物线y=-3x2+6x+2的对称轴是( )
A.直线x=2 B.直线x=-2 C.直线x=1 D.直线x=-1
46、将二次函数y=x2-2x-2化成y=a(x-h)2+k的形式为( )
A.y=(x-2)2-2 B.y=(x-1)2-3 C.y=(x-1)2-2 D.y=(x-2)2-3
47、将抛物线y=x2-6x+5向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
48、二次函数y=-2x2-4x+5的最大值是 .
49、若抛物线y=x2-bx+9的顶点在x轴负半轴上,则b的值为 .
50、已知二次函数y=x2+2mx+2,当x>2时,y的值随x的增大而增大,则实数m的取值范围是 .
51、设二次函数y=(ax-2)(x-2a),其中a是常数.
(1)当a=2时,试判断点(1,0)是否在该函数图象上;
(2)用含a的代数式表示函数图象的对称轴;
52、在平面直角坐标系xOy中,点(1,m)和点(3,n)在二次函数y=x2+bx的图象上.
(1)当m=-3时:
①求这个二次函数的顶点坐标;
②若点(-1,y1),(a,y2)在此二次函数的图象上,且y2>y1,则a的取值范围是多少?
(2)当mn<0时,求b的取值范围
