5.2.2平行线的判定 课件(共23张PPT)
文档属性
| 名称 | 5.2.2平行线的判定 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 902.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第5.2.2平行线的判定
人教版数学七年级下册
1.掌握平行线的三种判定方法,并初步运用它们进行简单的推理论证;
2.经历判定直线平行方法的探究过程,初步学会简单的论证和推理;
3.初步了解转化的数学思想方法.
学习目标
在同一平面内,不相交的两条直线叫做平行线.
平行线的定义:
我们通常用“//”表示平行.
平行线的表示法:
C
B
A
D
a∥b
AB∥CD
读作:“AB平行于CD”
读作:“a平行于b”
a
b
复习引入
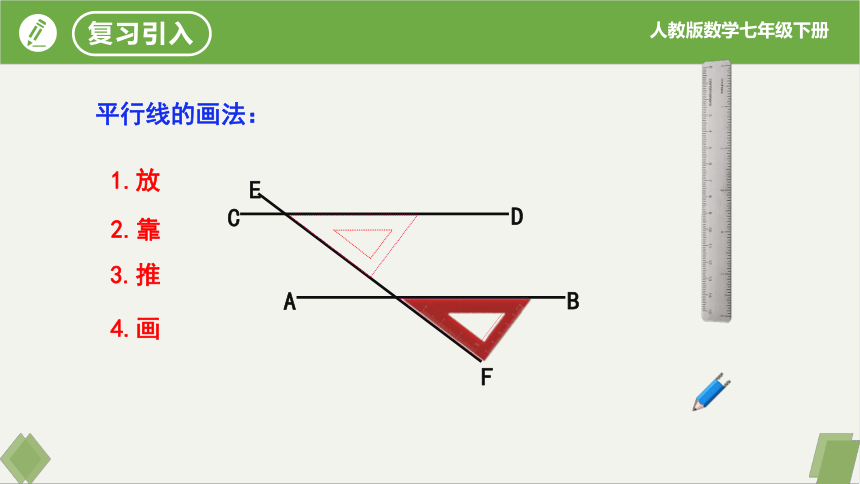
平行线的画法:
C
E
A
B
F
D
1.放
2.靠
3.推
4.画
复习引入
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
探究新知
C
E
A
B
F
D
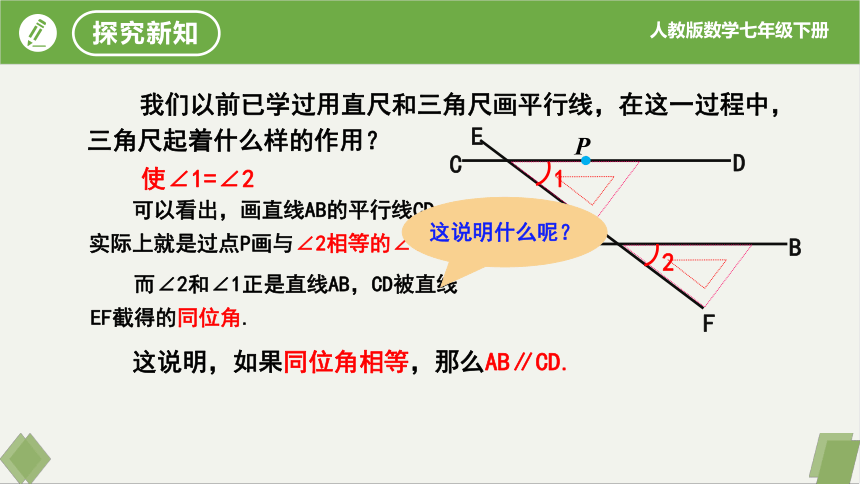
我们以前已学过用直尺和三角尺画平行线,在这一过程中,三角尺起着什么样的作用?
2
1
使∠1=∠2
P.
可以看出,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1.
而∠2和∠1正是直线AB,CD被直线EF截得的同位角.
这说明什么呢?
这说明,如果同位角相等,那么AB∥CD.
探究新知
判定两条直线平行的方法:
判定方法1:
两条直线被第三条直线所截,如果同位角相等, 那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
符号语言表示:
2
b
a
1
3
探究新知
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
探究新知
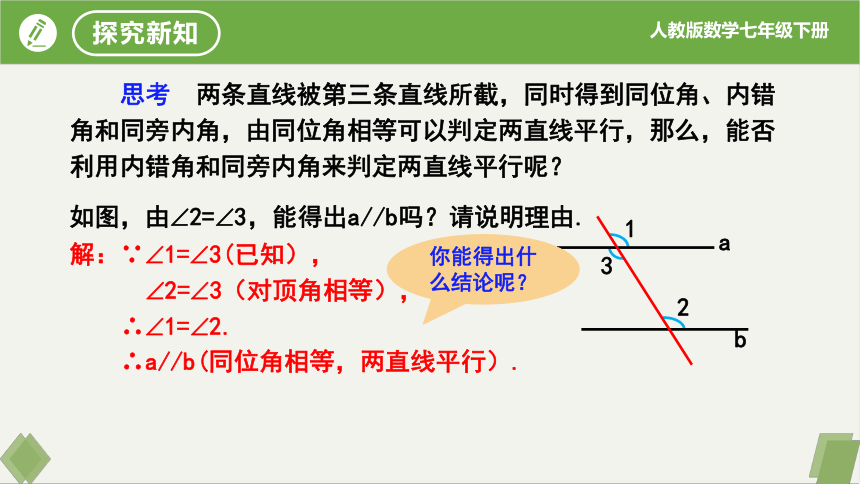
思考 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 2= 3,能得出a//b吗?请说明理由.
解:∵ 1= 3(已知),
2= 3(对顶角相等),
∴ 1= 2.
∴a//b(同位角相等,两直线平行).
2
b
a
1
3
你能得出什么结论呢?
探究新知
判定两条直线平行的方法:
判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠2=∠3(已知)
∴a∥b(内错角相等,两直线平行)
符号语言表示:
2
b
a
1
3
探究新知
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用同位角知识证明)
解:∵∠2+∠4 =180°,∠1+∠4 =180°
∴∠1=∠2(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
如图,已知∠2+∠4=180°,试说明a∥b.
2
b
a
1
3
4
你能得出什么结论呢?
探究新知
2
b
a
1
3
4
判定两条直线平行的方法:
判定方法3:
∵∠2+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
符号语言表示:
探究新知
例 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
b
c
a
1
2
解:这两条直线平行.
∵ b⊥a,c ⊥a
∴∠1=∠2=90°
∴b∥c(同位角相等,两直线平行)
结论:在同一平面内,垂直于同一条直线的两条直线互相平行.
例题讲解
随堂检测
1.如图,∠1=120°,要使 a//b,则∠2的大小是( )
A.60° B.80°
C.100° D.120°
D
2.如图,已知∠1=∠2,∠3=40°,则∠B的度数是( )
A.20° B.30°
C.40° D.60°
C
3.如图,下列条件中能得到AB∥CD的是( )
A. B.
C. D.
C
随堂检测
1.如图,有以下四个条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定AB∥CD的条件有( )
A.1个 B.2个
C.3个 D.4个
C
3
1
A
B
C
D
E
2
4
5
巩固练习
2.如图:
如果∠B=∠1,则可得____//___
根据是_____________________
如果∠D=∠1,则可得到____//___
根据是_______________________
BC
同位角相等,两直线平行
CD
内错角相等,两直线平行
AD
AB
巩固练习
解:∵∠2=∠5,(对顶角相等)
∠2=105°,(已知)
∴ ∠5=105°. (等量代换)
∵ ∠1=75°,(已知)
∴ ∠1+∠5=180°,
∴ AB//CD.(同旁内角互补,两直线平行)
3.如图,已知 ∠1=75° ,∠2 =105°. AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
巩固练习
1.如图,已知∠1=∠2,∠3=∠4,试判断直线EF与GH是否平行,并说明理由.
解:EF与GH平行.理由如下:
∵∠1=∠2,∠2=∠5(已知)
∴∠1=∠5(等量代换)
∵∠3=∠4 (已知)
∴∠1+∠3=∠4+∠5(等量加等量和相等)
即∠MEF=∠HGE
∴EF∥HG(同位角相等,两直线平行)
拓展训练
1.同位角相等,两直线平行.
3.同旁内角互补,两直线平行.
2.内错角相等,两直线平行.
4.在同一平面内,垂直于同一条直线的两条直线互相平行.
平行线的判定
课堂小结
1.如图,下列条件中,能判定AB∥CD的是( )
A.∠2=∠4
B.∠1=∠3
C.∠C=∠5
D.∠A=∠4
B
课后作业
2.如图:
如果∠1=∠D,那么______∥________;
如果∠1=∠B,那么______∥________;
如果∠A+∠B=180°,那么______∥________;
如果∠A+∠D=180°,那么______∥________.
AD
BC
AB
CD
AD
BC
AB
CD
1
A
B
D
C
课后作业
谢谢聆听
第5.2.2平行线的判定
人教版数学七年级下册
1.掌握平行线的三种判定方法,并初步运用它们进行简单的推理论证;
2.经历判定直线平行方法的探究过程,初步学会简单的论证和推理;
3.初步了解转化的数学思想方法.
学习目标
在同一平面内,不相交的两条直线叫做平行线.
平行线的定义:
我们通常用“//”表示平行.
平行线的表示法:
C
B
A
D
a∥b
AB∥CD
读作:“AB平行于CD”
读作:“a平行于b”
a
b
复习引入
平行线的画法:
C
E
A
B
F
D
1.放
2.靠
3.推
4.画
复习引入
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行.
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据两条直线是否相交来判定是否平行,那么有没有其他判定方法呢?
探究新知
C
E
A
B
F
D
我们以前已学过用直尺和三角尺画平行线,在这一过程中,三角尺起着什么样的作用?
2
1
使∠1=∠2
P.
可以看出,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1.
而∠2和∠1正是直线AB,CD被直线EF截得的同位角.
这说明什么呢?
这说明,如果同位角相等,那么AB∥CD.
探究新知
判定两条直线平行的方法:
判定方法1:
两条直线被第三条直线所截,如果同位角相等, 那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
符号语言表示:
2
b
a
1
3
探究新知
你能说出木工师傅用图中的角尺工具画平行线的道理吗?
同位角相等,两直线平行.
探究新知
思考 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 2= 3,能得出a//b吗?请说明理由.
解:∵ 1= 3(已知),
2= 3(对顶角相等),
∴ 1= 2.
∴a//b(同位角相等,两直线平行).
2
b
a
1
3
你能得出什么结论呢?
探究新知
判定两条直线平行的方法:
判定方法2:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠2=∠3(已知)
∴a∥b(内错角相等,两直线平行)
符号语言表示:
2
b
a
1
3
探究新知
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用同位角知识证明)
解:∵∠2+∠4 =180°,∠1+∠4 =180°
∴∠1=∠2(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
如图,已知∠2+∠4=180°,试说明a∥b.
2
b
a
1
3
4
你能得出什么结论呢?
探究新知
2
b
a
1
3
4
判定两条直线平行的方法:
判定方法3:
∵∠2+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
符号语言表示:
探究新知
例 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
b
c
a
1
2
解:这两条直线平行.
∵ b⊥a,c ⊥a
∴∠1=∠2=90°
∴b∥c(同位角相等,两直线平行)
结论:在同一平面内,垂直于同一条直线的两条直线互相平行.
例题讲解
随堂检测
1.如图,∠1=120°,要使 a//b,则∠2的大小是( )
A.60° B.80°
C.100° D.120°
D
2.如图,已知∠1=∠2,∠3=40°,则∠B的度数是( )
A.20° B.30°
C.40° D.60°
C
3.如图,下列条件中能得到AB∥CD的是( )
A. B.
C. D.
C
随堂检测
1.如图,有以下四个条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定AB∥CD的条件有( )
A.1个 B.2个
C.3个 D.4个
C
3
1
A
B
C
D
E
2
4
5
巩固练习
2.如图:
如果∠B=∠1,则可得____//___
根据是_____________________
如果∠D=∠1,则可得到____//___
根据是_______________________
BC
同位角相等,两直线平行
CD
内错角相等,两直线平行
AD
AB
巩固练习
解:∵∠2=∠5,(对顶角相等)
∠2=105°,(已知)
∴ ∠5=105°. (等量代换)
∵ ∠1=75°,(已知)
∴ ∠1+∠5=180°,
∴ AB//CD.(同旁内角互补,两直线平行)
3.如图,已知 ∠1=75° ,∠2 =105°. AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
巩固练习
1.如图,已知∠1=∠2,∠3=∠4,试判断直线EF与GH是否平行,并说明理由.
解:EF与GH平行.理由如下:
∵∠1=∠2,∠2=∠5(已知)
∴∠1=∠5(等量代换)
∵∠3=∠4 (已知)
∴∠1+∠3=∠4+∠5(等量加等量和相等)
即∠MEF=∠HGE
∴EF∥HG(同位角相等,两直线平行)
拓展训练
1.同位角相等,两直线平行.
3.同旁内角互补,两直线平行.
2.内错角相等,两直线平行.
4.在同一平面内,垂直于同一条直线的两条直线互相平行.
平行线的判定
课堂小结
1.如图,下列条件中,能判定AB∥CD的是( )
A.∠2=∠4
B.∠1=∠3
C.∠C=∠5
D.∠A=∠4
B
课后作业
2.如图:
如果∠1=∠D,那么______∥________;
如果∠1=∠B,那么______∥________;
如果∠A+∠B=180°,那么______∥________;
如果∠A+∠D=180°,那么______∥________.
AD
BC
AB
CD
AD
BC
AB
CD
1
A
B
D
C
课后作业
谢谢聆听
