5.3.1平行线的性质 课件(共19张PPT)
文档属性
| 名称 | 5.3.1平行线的性质 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 719.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第5.3.1平行线的性质
人教版数学七年级下册
1.理解平行线的性质;
2.能初步运用平行线的性质进行有关计算;
3.体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力.
学习目标
判定两条直线平行的方法:
1.同位角相等,两直线平行.
3.同旁内角互补,两直线平行.
2.内错角相等,两直线平行.
两直线平行
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习引入
7
1
2
3
4
5
6
8
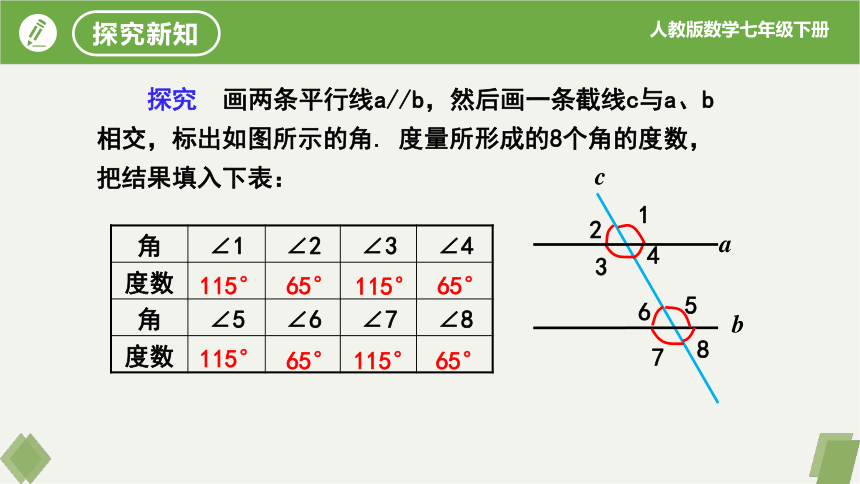
探究 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
探究新知
7
1
2
3
4
5
6
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
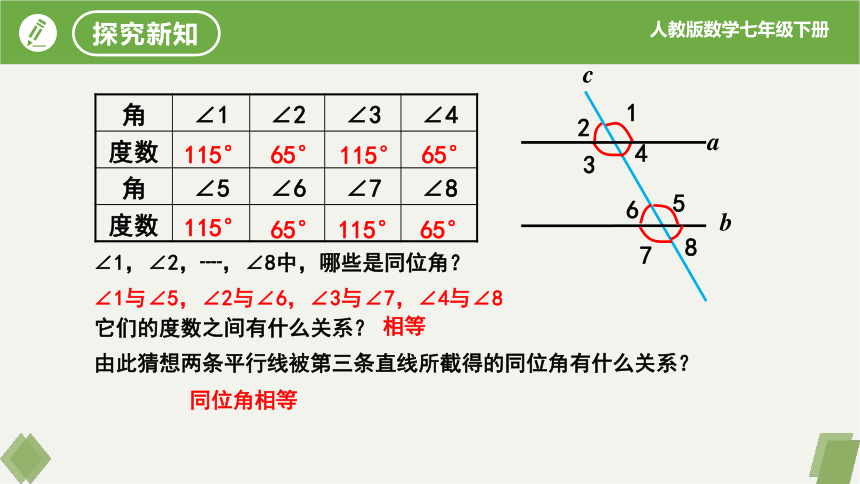
∠1,∠2,┈,∠8中,哪些是同位角?
它们的度数之间有什么关系?
由此猜想两条平行线被第三条直线所截得的同位角有什么关系?
∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8
相等
同位角相等
探究新知
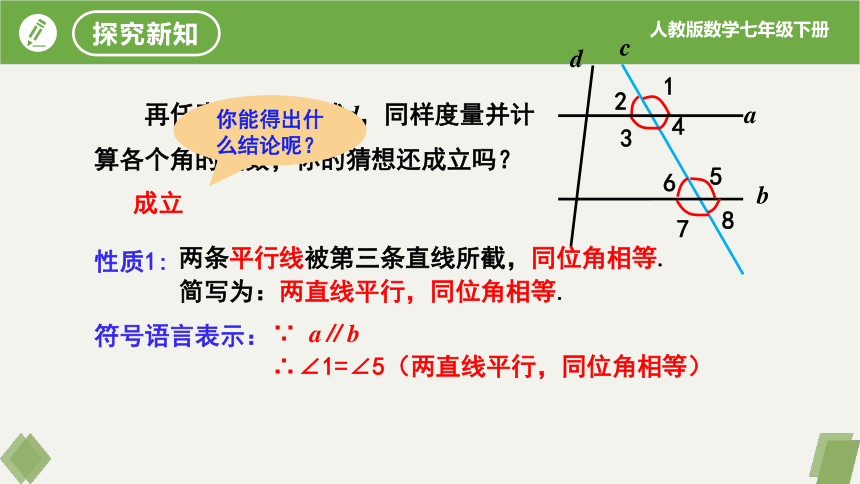
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
7
1
2
3
4
5
6
8
a
b
c
d
成立
你能得出什么结论呢?
性质1:
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
符号语言表示:
∵ a∥b
∴∠1=∠5(两直线平行,同位角相等)
探究新知
思考:上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似的,你能由性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
如图,已知a//b,那么 1与 2相等吗?为什么
∵a∥b(已知)
∴∠2=∠3 (两直线平行,同位角相等)
∵∠1=∠3 (对顶角相等)
∴∠1=∠2 (等量代换)
b
1
2
a
c
3
∠1=∠2 理由如下:
解:
你能得出什么结论呢?
探究新知
性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
符号语言表示:
∵ a∥b
∴∠1=∠2(两直线平行,内错角相等)
b
1
2
a
c
3
探究新知
如图,已知a//b,那么 2与 4有什么关系呢?为什么
∴ 2+ 4=180°(等量代换)
思考:
类似的,已知两直线平行,能否得到同旁内角之间的数量关系?
2和 4互补.理由如下:
解:
b
1
2
a
c
3
∵a//b(已知)
∴ 2= 3(两直线平行,同位角相等)
∵ 3+ 4=180°(邻补角定义)
4
你能得出什么结论呢?
探究新知
b
1
2
a
c
3
4
性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
符号语言表示:
∵ a∥b
∴∠2+∠4=180°(两直线平行,同旁内角互补)
探究新知
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,
所以∠A与∠D互补,∠B与∠C互补.
所以梯形的另外两个角分别是80°,65°.
于是∠D=180°-∠A=180°-100°=80°
∠C= 180°-∠B=180°-115°=65°
例题讲解
随堂检测
1.如图,直线a∥b,c是截线,若∠1=50°,则∠2= ( )
A.40° B.45° C.50° D.55°
2.如图,AB∥CD,直线EF分别交AB,CD于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=80°,则∠PNM等于 ( )
A.15° B.25° C.35° D.45°
C
C
1.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )
A.50° B.45° C.30° D.40°
D
2.如图,已知CD∥BE, 如果∠1=60°, 那么∠B的度数为( )
A.70° B.100° C.110° D.120°
D
巩固练习
3.光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,若∠1=48°,∠2=158°,则∠3的度数为 ( )
A.68° B.70°
C.78° D.80°
4.如图,CD//AB,点 O 在 AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )
A.20° B.25°
C.30° D.35°
B
D
巩固练习
5.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的∠B是142o,第二次拐的∠C是多少度?为什么?
解:∠C=142o
∵两直线平行,内错角相等.
巩固练习
拓展训练
1.如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.
(1)求∠1+∠2的度数;(2)若∠2=40°,求∠3的度数.
解:(1)因为BF,DE分别平分∠ABD和∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为AB∥CD,所以∠ABD+∠BDC=180°,
即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,
由(1)知∠1+∠2=90°,
所以∠1=90°-∠2=50°.
因为AB∥CD,所以∠1+∠3=180°,
所以∠3=180°-∠1=130°.
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
课堂小结
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
1.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
课后作业
谢谢聆听
第5.3.1平行线的性质
人教版数学七年级下册
1.理解平行线的性质;
2.能初步运用平行线的性质进行有关计算;
3.体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力.
学习目标
判定两条直线平行的方法:
1.同位角相等,两直线平行.
3.同旁内角互补,两直线平行.
2.内错角相等,两直线平行.
两直线平行
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习引入
7
1
2
3
4
5
6
8
探究 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
探究新知
7
1
2
3
4
5
6
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
115°
115°
115°
115°
65°
65°
65°
65°
∠1,∠2,┈,∠8中,哪些是同位角?
它们的度数之间有什么关系?
由此猜想两条平行线被第三条直线所截得的同位角有什么关系?
∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8
相等
同位角相等
探究新知
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
7
1
2
3
4
5
6
8
a
b
c
d
成立
你能得出什么结论呢?
性质1:
两条平行线被第三条直线所截,同位角相等.
简写为:两直线平行,同位角相等.
符号语言表示:
∵ a∥b
∴∠1=∠5(两直线平行,同位角相等)
探究新知
思考:上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”,类似的,你能由性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
如图,已知a//b,那么 1与 2相等吗?为什么
∵a∥b(已知)
∴∠2=∠3 (两直线平行,同位角相等)
∵∠1=∠3 (对顶角相等)
∴∠1=∠2 (等量代换)
b
1
2
a
c
3
∠1=∠2 理由如下:
解:
你能得出什么结论呢?
探究新知
性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:两直线平行,内错角相等.
符号语言表示:
∵ a∥b
∴∠1=∠2(两直线平行,内错角相等)
b
1
2
a
c
3
探究新知
如图,已知a//b,那么 2与 4有什么关系呢?为什么
∴ 2+ 4=180°(等量代换)
思考:
类似的,已知两直线平行,能否得到同旁内角之间的数量关系?
2和 4互补.理由如下:
解:
b
1
2
a
c
3
∵a//b(已知)
∴ 2= 3(两直线平行,同位角相等)
∵ 3+ 4=180°(邻补角定义)
4
你能得出什么结论呢?
探究新知
b
1
2
a
c
3
4
性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:两直线平行,同旁内角互补.
符号语言表示:
∵ a∥b
∴∠2+∠4=180°(两直线平行,同旁内角互补)
探究新知
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
解:因为梯形上、下底互相平行,
所以∠A与∠D互补,∠B与∠C互补.
所以梯形的另外两个角分别是80°,65°.
于是∠D=180°-∠A=180°-100°=80°
∠C= 180°-∠B=180°-115°=65°
例题讲解
随堂检测
1.如图,直线a∥b,c是截线,若∠1=50°,则∠2= ( )
A.40° B.45° C.50° D.55°
2.如图,AB∥CD,直线EF分别交AB,CD于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=80°,则∠PNM等于 ( )
A.15° B.25° C.35° D.45°
C
C
1.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )
A.50° B.45° C.30° D.40°
D
2.如图,已知CD∥BE, 如果∠1=60°, 那么∠B的度数为( )
A.70° B.100° C.110° D.120°
D
巩固练习
3.光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,若∠1=48°,∠2=158°,则∠3的度数为 ( )
A.68° B.70°
C.78° D.80°
4.如图,CD//AB,点 O 在 AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )
A.20° B.25°
C.30° D.35°
B
D
巩固练习
5.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的∠B是142o,第二次拐的∠C是多少度?为什么?
解:∠C=142o
∵两直线平行,内错角相等.
巩固练习
拓展训练
1.如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.
(1)求∠1+∠2的度数;(2)若∠2=40°,求∠3的度数.
解:(1)因为BF,DE分别平分∠ABD和∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
因为AB∥CD,所以∠ABD+∠BDC=180°,
即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,
由(1)知∠1+∠2=90°,
所以∠1=90°-∠2=50°.
因为AB∥CD,所以∠1+∠3=180°,
所以∠3=180°-∠1=130°.
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
课堂小结
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
1.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
课后作业
谢谢聆听
