【2024春人教七下数学高效实用备课】5_1_1相交线 课件(共26张PPT)
文档属性
| 名称 | 【2024春人教七下数学高效实用备课】5_1_1相交线 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
人教七下数学同步精品课件
人教版七年级下册
5.1.1 相交线
第五章 相交线与平行线
章首引入
同学们对两条直线相交、平行一定不陌生吧!纵横交错的道路,棋盘中的横线和竖线,操场上的双杠,教室中的课桌面、黑板面相邻的两条边与相对的两条边……都给我们以相交线或平行线的形象.你能再举出一些相交线和平行线的实例吗
章首引入
本章将研究平面内不重合的两条直线的位置关系:相交与平行.
对于相交,我们要研究两条直线相交所成的角的位置关系和数量关系;对于平行,我们要借助于一条直线与另外两条直线相交所成的角,研究平行线的判定和性质.在此基础上,再学习平移的有关知识.本章我们还将学习通过简单的推理得出数学结论的方法,培养言之有据的思考习惯.
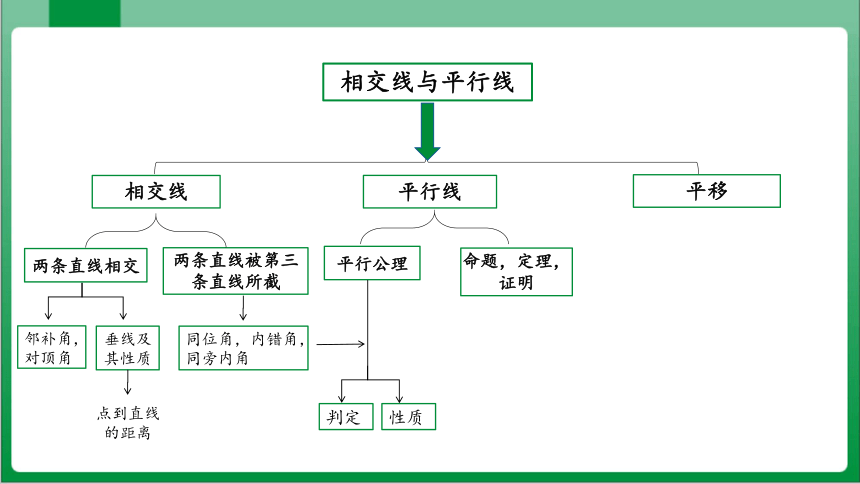
相交线与平行线
相交线
平行线
平移
两条直线被第三条直线所截
邻补角,对顶角
垂线及其性质
两条直线相交
同位角,内错角,同旁内角
命题,定理,证明
平行公理
判定
点到直线的距离
性质
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能准确识别邻补角与对顶角.
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.
重点
难点
同学们对相交线应该不陌生,生活中处处充满着相交,你能发现吗?
新课引入
观察由剪刀形成的相交线.
探究
A
C
O
D
B
新知学习
一 邻补角与对顶角的概念
思考:1. 任意两条直线相交,能形成几个小于平角的角呢?
A
C
O
D
B
1
2
3
4
2. ∠1 和 ∠2 有怎样的位置关系?
四个,分别是如图所示∠1、∠2、∠3 和∠4.
∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线.
3. ∠1 和 ∠3 有怎样的位置关系?
∠1 和∠3 有一个公共顶点 O,并且∠1 的两条边分别是∠3 的两边的反向延长线.
归纳
如图,∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线(∠1 和∠2互补),具有这种关系的两个角,互为邻补角;
∠1 和∠3 有一个公共顶点 O,并且∠1 的两条边分别是∠3 的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
C
O
D
B
1
2
3
4
邻补角的概念:
如果两个角有一条公共边,它们的另一边互为_____________,那么这两个角互为邻补角.
图中∠1 的邻补角有 ___________.
A
C
O
D
B
1
2
3
4
反向延长线
∠2,∠4
图中共有_____对邻补角,分别是_
__________________________________
__________________________________
4
∠1与∠2;∠2与∠3;
∠3与∠4;∠4与∠1.
对顶角的概念:
如果两个角有一个公共顶点,并且其中一个角的两边分别是另一个角的两边的 _____________,那么这两个角互为对顶角.
图中∠2的对顶角是 __________.
A
C
O
D
B
1
2
3
4
反向延长线
∠4
图中共有______对对顶角,分别是
_________________________________
2
∠1与∠3;∠2与∠4
例1 如图所示,∠1 与∠2 互为邻补角的是 ( )
D
例2 下列各图中,∠1 与∠2 是对顶角的是 ( )
D
提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.
A
C
D
B
O
1
2
3
4
探究
当直线 CD 绕着点 O 顺时针旋转时,∠1 与 ∠2 的位置关系有变化吗?∠1 与 ∠3 呢?
C
D
1
2
3
4
位置关系都不变,即
∠1 与 ∠2 互为邻补角;
∠1 与 ∠3 互为对顶角.
二 对顶角的性质
A
C
O
D
B
1
2
3
4
∠1 与 ∠2 有什么数量关系?∠1 与 ∠3 呢?
同理:因为∠2+∠3=180°
所以∠1=∠3 (同角的补角相等)
平角180°
解析:因为∠1+∠2=∠AOB
且∠AOB=180°
所以∠1+∠2=180°
归纳
邻补角、对顶角的性质:
邻补角互补;
∠1+∠2=180°;∠2+∠3=180°;∠3+∠4=180°;∠4+∠1=180°;
对顶角相等.
∠1=∠3;∠2=∠4;
A
C
O
D
B
1
2
3
4
例3 如图,直线 a,b 相交,∠1 = 40°,求∠2、∠3、∠4 的度数.
解:由邻补角的定义,得
∠2 = 180° - ∠1 =180° - 40°= 140°
由对顶角相等,得
∠3 = ∠1 = 40°,
∠4 = ∠2 = 140°.
A
B
C
D
E
F
O
1.已知:如图,直线AB、CD、EF相交于点O.
1、∠AOE 的邻补角是_________________
2、∠COE的对顶角是__________________
3、图中共有邻补角_________对,共有对顶角_______对.
∠AOF和∠EOB
∠DOF
12
6
随堂练习
2.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
解:40°. 如图所示.
∵∠1与∠2是对顶角,
∴ ∠1=∠2=40°.
1
2
3.如图,直线 AB,CD,EF 相交于点 O,∠AOE = 40°,
∠BOC = 2∠AOC,求∠DOF 的度数.
解:设∠AOC = x,则∠BOC = 2x.
由邻补角的性质可得 x+2x = 180°,
解得 x = 60°,即∠AOC= 60°,
所以 ∠EOC=∠AOC- ∠AOE = 60°-40°= 20°,
由对顶角相等得 ∠DOF =∠EOC = 20°.
当题目中出现倍数关系时,可列方程来计算角.
角的名称 特征 性质 相同点 不同点
邻补角
对顶角
①两条直线相交形成的角;
②有公共顶点;
③有一条公共边.
①两条直线相交形成的角;
②有公共顶点;
③没有公共边.
邻补角互补
对顶角相等
①都是两条直线相交而成的角;
②都有一个公共顶点;
③都是成对出现的.
①有无公共边;
②两直线相交时,对顶角只有两对,邻补角有四对
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
5.1.1 相交线
第五章 相交线与平行线
章首引入
同学们对两条直线相交、平行一定不陌生吧!纵横交错的道路,棋盘中的横线和竖线,操场上的双杠,教室中的课桌面、黑板面相邻的两条边与相对的两条边……都给我们以相交线或平行线的形象.你能再举出一些相交线和平行线的实例吗
章首引入
本章将研究平面内不重合的两条直线的位置关系:相交与平行.
对于相交,我们要研究两条直线相交所成的角的位置关系和数量关系;对于平行,我们要借助于一条直线与另外两条直线相交所成的角,研究平行线的判定和性质.在此基础上,再学习平移的有关知识.本章我们还将学习通过简单的推理得出数学结论的方法,培养言之有据的思考习惯.
相交线与平行线
相交线
平行线
平移
两条直线被第三条直线所截
邻补角,对顶角
垂线及其性质
两条直线相交
同位角,内错角,同旁内角
命题,定理,证明
平行公理
判定
点到直线的距离
性质
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.能准确识别邻补角与对顶角.
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.
重点
难点
同学们对相交线应该不陌生,生活中处处充满着相交,你能发现吗?
新课引入
观察由剪刀形成的相交线.
探究
A
C
O
D
B
新知学习
一 邻补角与对顶角的概念
思考:1. 任意两条直线相交,能形成几个小于平角的角呢?
A
C
O
D
B
1
2
3
4
2. ∠1 和 ∠2 有怎样的位置关系?
四个,分别是如图所示∠1、∠2、∠3 和∠4.
∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线.
3. ∠1 和 ∠3 有怎样的位置关系?
∠1 和∠3 有一个公共顶点 O,并且∠1 的两条边分别是∠3 的两边的反向延长线.
归纳
如图,∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线(∠1 和∠2互补),具有这种关系的两个角,互为邻补角;
∠1 和∠3 有一个公共顶点 O,并且∠1 的两条边分别是∠3 的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
A
C
O
D
B
1
2
3
4
邻补角的概念:
如果两个角有一条公共边,它们的另一边互为_____________,那么这两个角互为邻补角.
图中∠1 的邻补角有 ___________.
A
C
O
D
B
1
2
3
4
反向延长线
∠2,∠4
图中共有_____对邻补角,分别是_
__________________________________
__________________________________
4
∠1与∠2;∠2与∠3;
∠3与∠4;∠4与∠1.
对顶角的概念:
如果两个角有一个公共顶点,并且其中一个角的两边分别是另一个角的两边的 _____________,那么这两个角互为对顶角.
图中∠2的对顶角是 __________.
A
C
O
D
B
1
2
3
4
反向延长线
∠4
图中共有______对对顶角,分别是
_________________________________
2
∠1与∠3;∠2与∠4
例1 如图所示,∠1 与∠2 互为邻补角的是 ( )
D
例2 下列各图中,∠1 与∠2 是对顶角的是 ( )
D
提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.
A
C
D
B
O
1
2
3
4
探究
当直线 CD 绕着点 O 顺时针旋转时,∠1 与 ∠2 的位置关系有变化吗?∠1 与 ∠3 呢?
C
D
1
2
3
4
位置关系都不变,即
∠1 与 ∠2 互为邻补角;
∠1 与 ∠3 互为对顶角.
二 对顶角的性质
A
C
O
D
B
1
2
3
4
∠1 与 ∠2 有什么数量关系?∠1 与 ∠3 呢?
同理:因为∠2+∠3=180°
所以∠1=∠3 (同角的补角相等)
平角180°
解析:因为∠1+∠2=∠AOB
且∠AOB=180°
所以∠1+∠2=180°
归纳
邻补角、对顶角的性质:
邻补角互补;
∠1+∠2=180°;∠2+∠3=180°;∠3+∠4=180°;∠4+∠1=180°;
对顶角相等.
∠1=∠3;∠2=∠4;
A
C
O
D
B
1
2
3
4
例3 如图,直线 a,b 相交,∠1 = 40°,求∠2、∠3、∠4 的度数.
解:由邻补角的定义,得
∠2 = 180° - ∠1 =180° - 40°= 140°
由对顶角相等,得
∠3 = ∠1 = 40°,
∠4 = ∠2 = 140°.
A
B
C
D
E
F
O
1.已知:如图,直线AB、CD、EF相交于点O.
1、∠AOE 的邻补角是_________________
2、∠COE的对顶角是__________________
3、图中共有邻补角_________对,共有对顶角_______对.
∠AOF和∠EOB
∠DOF
12
6
随堂练习
2.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数吗?你能说出所量角的度数是多少吗?为什么?
解:40°. 如图所示.
∵∠1与∠2是对顶角,
∴ ∠1=∠2=40°.
1
2
3.如图,直线 AB,CD,EF 相交于点 O,∠AOE = 40°,
∠BOC = 2∠AOC,求∠DOF 的度数.
解:设∠AOC = x,则∠BOC = 2x.
由邻补角的性质可得 x+2x = 180°,
解得 x = 60°,即∠AOC= 60°,
所以 ∠EOC=∠AOC- ∠AOE = 60°-40°= 20°,
由对顶角相等得 ∠DOF =∠EOC = 20°.
当题目中出现倍数关系时,可列方程来计算角.
角的名称 特征 性质 相同点 不同点
邻补角
对顶角
①两条直线相交形成的角;
②有公共顶点;
③有一条公共边.
①两条直线相交形成的角;
②有公共顶点;
③没有公共边.
邻补角互补
对顶角相等
①都是两条直线相交而成的角;
②都有一个公共顶点;
③都是成对出现的.
①有无公共边;
②两直线相交时,对顶角只有两对,邻补角有四对
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
