【2024春人教七下数学高效实用备课】5_5_数学活动 课件(共21张PPT)
文档属性
| 名称 | 【2024春人教七下数学高效实用备课】5_5_数学活动 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
人教七下数学同步精品课件
人教版七年级下册
5.5 数学活动
第五章 相交线与平行线
章末小结
1. 用平行线的判定方法画平行线;
2. 利用平移知识设计美丽的图案.
学习目标
重点
难点
新知学习
活动1 你有多少种画平行线的方法?
学行线后,李强、张明、王玲三位同学分别想出了过一点画一条直线的平行线的新的方法,他们分别是这样做的:
李强
过点 P 作直线 b
(2)
(1)
则 c∥a
(4)
作∠2 =∠1
(3)
你知道他这样做的道理吗?
类似地,你在画平行线的方法上受到了什么启发?
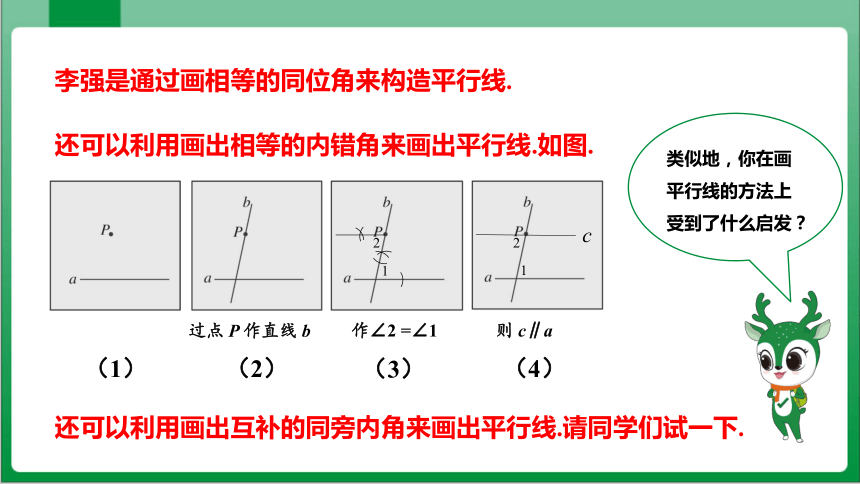
李强是通过画相等的同位角来构造平行线.
还可以利用画出相等的内错角来画出平行线.如图.
过点 P 作直线 b
(2)
(1)
1
2
作∠2 =∠1
(3)
则 c∥a
(4)
1
2
c
还可以利用画出互补的同旁内角来画出平行线.请同学们试一下.
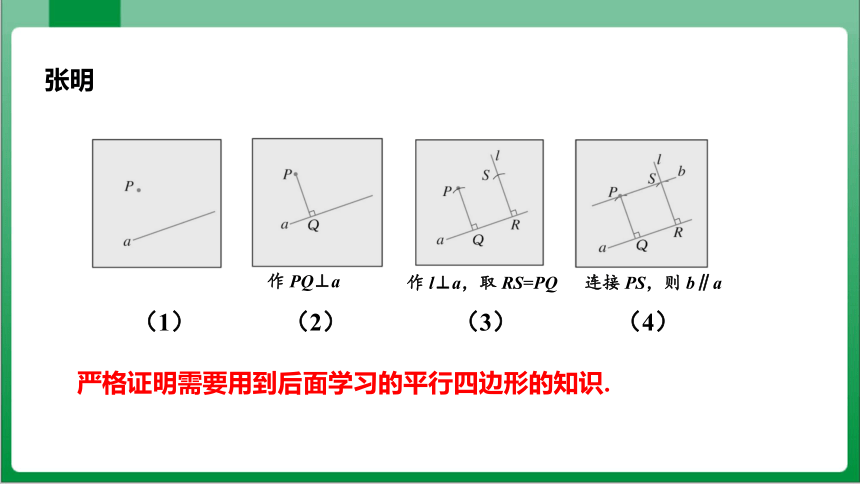
张明
作 PQ⊥a
(2)
(1)
(3)
连接 PS,则 b∥a
(4)
作 l⊥a,取 RS=PQ
严格证明需要用到后面学行四边形的知识.
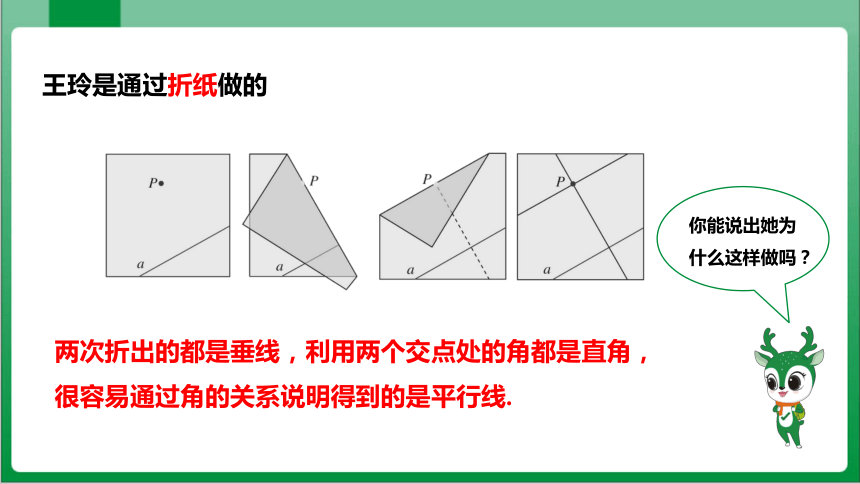
王玲是通过折纸做的
你能说出她为什么这样做吗?
两次折出的都是垂线,利用两个交点处的角都是直角,很容易通过角的关系说明得到的是平行线.
你还有其他方法吗?动手试一试,与同学们交流一下.
思考
活动2 设计美丽的图案
利用平移,可以设计非常美丽的图案.例如图中的每一匹马都可以由正方形上的平移得到.
类似地,你还能用平移设计一些图案吗?
正方形
相框
长方形
平行四边形
沙漏
狐狸
相交线与平行线
相交线
邻补角: 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;
对顶角:有一个公共顶点,并且它们的两条边分别互为反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角性质:对顶角相等.
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
相交线
垂线
垂线的画法:1贴;2靠;3移;4画.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
同位角,内错角,同旁内角
同位角:位于截线的同侧,且都位于两条被截线的同一方,具有这种位置关系的一对角叫做同位角.
内错角:位于两条被截直线之间,且分别位于截线两侧,具有这种位置关系的一对角叫做内错角.
同旁内角:位于截线的同一旁,且都位于两条被截直线之间,具有这种位置关系的一对角叫做同旁内角.
章末小结
相交线与平行线
平行线
定义: 在同一平面内,直线 a 与直线 b 不相交时,我们说直线 a 与 b 互相平行.
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判定方法2:内错角相等,两直线平行.
判定方法1:同位角相等,两直线平行.
平行线
平行线的判定
判定方法3:同旁内角互补,两直线平行.
性质1:两直线平行,同位角相等.
命题,定理,证明
命题:像这样判断一件事情的语句,叫做命题.
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题;
假命题:题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
定理:它们的正确性是经过推理证实的,这样得到的真命题叫做定理.
平行线的性质
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
证明:一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明
相交线与平行线
平移
定义: 把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动叫做平移.
平移性质:1. 平移前后的两个图形形状和大小完全相同;
2. 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行 (或在同一直线上) 且相等;
平移两要素:平移的方向;平移的距离.
平移作图的步骤:1定;2找;3移;4连.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
5.5 数学活动
第五章 相交线与平行线
章末小结
1. 用平行线的判定方法画平行线;
2. 利用平移知识设计美丽的图案.
学习目标
重点
难点
新知学习
活动1 你有多少种画平行线的方法?
学行线后,李强、张明、王玲三位同学分别想出了过一点画一条直线的平行线的新的方法,他们分别是这样做的:
李强
过点 P 作直线 b
(2)
(1)
则 c∥a
(4)
作∠2 =∠1
(3)
你知道他这样做的道理吗?
类似地,你在画平行线的方法上受到了什么启发?
李强是通过画相等的同位角来构造平行线.
还可以利用画出相等的内错角来画出平行线.如图.
过点 P 作直线 b
(2)
(1)
1
2
作∠2 =∠1
(3)
则 c∥a
(4)
1
2
c
还可以利用画出互补的同旁内角来画出平行线.请同学们试一下.
张明
作 PQ⊥a
(2)
(1)
(3)
连接 PS,则 b∥a
(4)
作 l⊥a,取 RS=PQ
严格证明需要用到后面学行四边形的知识.
王玲是通过折纸做的
你能说出她为什么这样做吗?
两次折出的都是垂线,利用两个交点处的角都是直角,很容易通过角的关系说明得到的是平行线.
你还有其他方法吗?动手试一试,与同学们交流一下.
思考
活动2 设计美丽的图案
利用平移,可以设计非常美丽的图案.例如图中的每一匹马都可以由正方形上的平移得到.
类似地,你还能用平移设计一些图案吗?
正方形
相框
长方形
平行四边形
沙漏
狐狸
相交线与平行线
相交线
邻补角: 有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;
对顶角:有一个公共顶点,并且它们的两条边分别互为反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角性质:对顶角相等.
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
相交线
垂线
垂线的画法:1贴;2靠;3移;4画.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
同位角,内错角,同旁内角
同位角:位于截线的同侧,且都位于两条被截线的同一方,具有这种位置关系的一对角叫做同位角.
内错角:位于两条被截直线之间,且分别位于截线两侧,具有这种位置关系的一对角叫做内错角.
同旁内角:位于截线的同一旁,且都位于两条被截直线之间,具有这种位置关系的一对角叫做同旁内角.
章末小结
相交线与平行线
平行线
定义: 在同一平面内,直线 a 与直线 b 不相交时,我们说直线 a 与 b 互相平行.
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判定方法2:内错角相等,两直线平行.
判定方法1:同位角相等,两直线平行.
平行线
平行线的判定
判定方法3:同旁内角互补,两直线平行.
性质1:两直线平行,同位角相等.
命题,定理,证明
命题:像这样判断一件事情的语句,叫做命题.
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题;
假命题:题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
定理:它们的正确性是经过推理证实的,这样得到的真命题叫做定理.
平行线的性质
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
证明:一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明
相交线与平行线
平移
定义: 把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动叫做平移.
平移性质:1. 平移前后的两个图形形状和大小完全相同;
2. 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行 (或在同一直线上) 且相等;
平移两要素:平移的方向;平移的距离.
平移作图的步骤:1定;2找;3移;4连.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
