7.2 正弦、余弦(第1课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 7.2 正弦、余弦(第1课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
第7章 锐角三角函数
7.2 正弦、余弦(1)
第1课时 正弦、余弦
学习目标
1.理解并掌握正弦、余弦的概念,会在直角三角形中求一个锐角的正弦和余弦;
2.了解正弦、余弦值随锐角增大时的变化规律;
3.会用计算器求锐角的正弦值、余弦值.
实践与探索
5m
13m
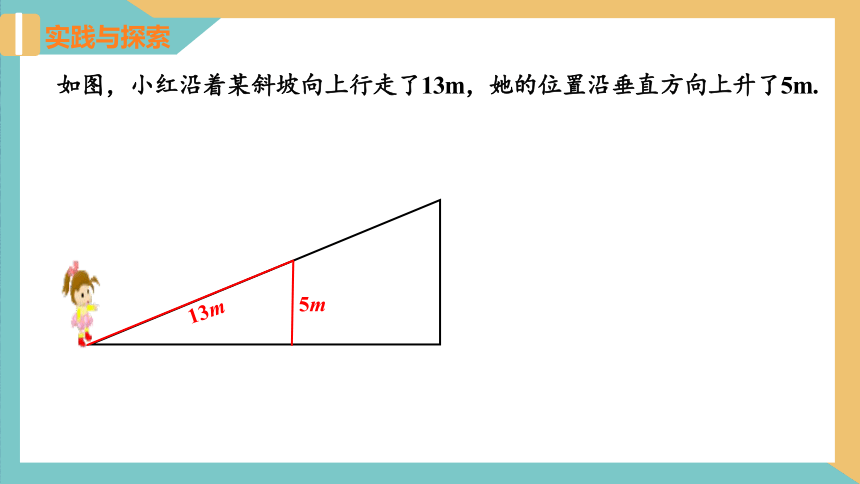
如图,小红沿着某斜坡向上行走了13m,她的位置沿垂直方向上升了5m.
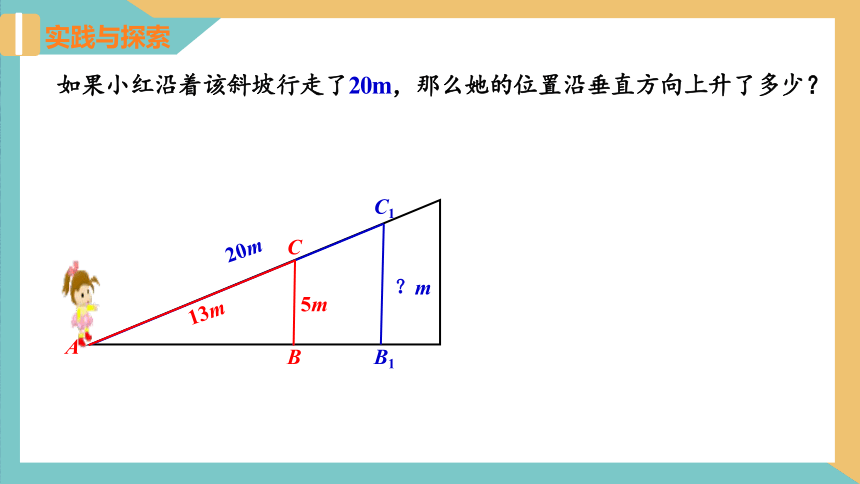
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
20m
?m
5m
13m
C
B
A
C1
B1
20m
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
?m
5m
13m
C
B
A
C1
B1
=
=
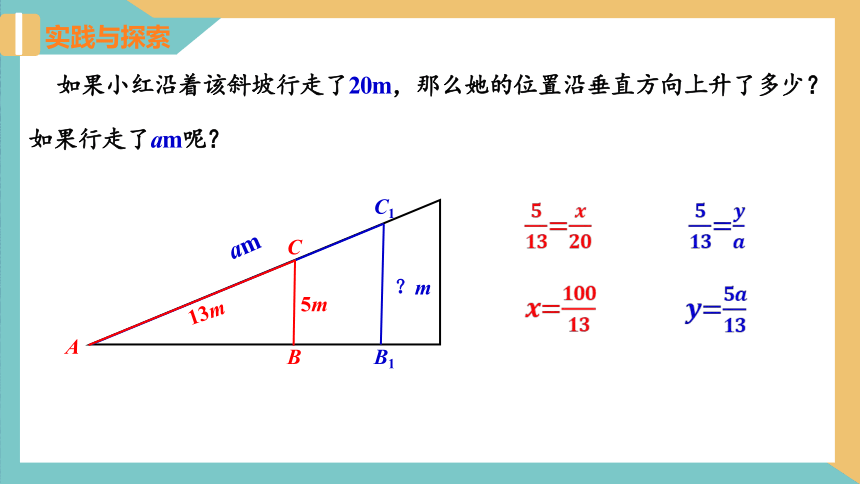
如果行走了am呢?
=
=
am
20m
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
m
5m
13m
C
B
A
C1
B1
在上述情形中,小明的位置沿水平方向又分别前进了多少?
12m
m
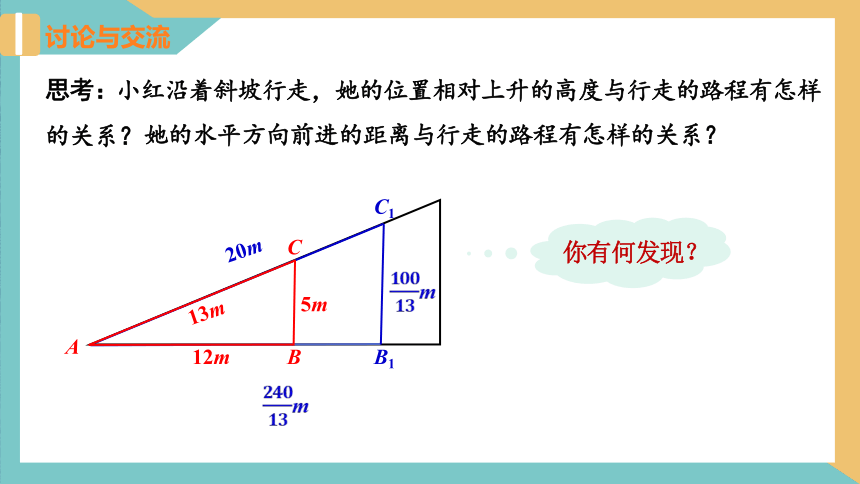
小红沿着斜坡行走,她的位置相对上升的高度与行走的路程有怎样的关系?
20m
思考:
讨论与交流
m
5m
13m
C
B
A
B1
她的水平方向前进的距离与行走的路程有怎样的关系?
12m
m
C1
你有何发现?
从上面的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值________;它的邻边与斜边的比值_________. (根据是_____________________)
归纳与总结
20m
m
5m
13m
C
B
A
B1
12m
m
C1
不变
不变
相似三角形的性质
概念学习
如图,在Rt△ABC中,∠C=90°,我们把∠A的对边a与斜边c的比叫做∠A的正弦(sine),记作sinA,
A
B
C
斜边c
对边a
邻边b
即 sinA==.
我们把∠A的邻边b与斜边c的比叫做∠A的余弦(cosine),
记作cosA,
即 cosA==.
你能写出∠B的正弦、余弦的表达式吗?
概念学习
在Rt△ABC中,、和的值都随∠A的大小变化而变化,都随∠A的大小确定而唯一确定. ∠A的正弦、余弦和正切都是∠A的三角函数.
A
B
C
斜边c
对边a
邻边b
三
角
函
数
正弦
正切
余弦
sinA==
cosA==
tanA==
概念中的几个注意点:
概念学习
(1)是在直角三角形中定义的,∠A是一个锐角;
(2)是一个完整的符号,习惯省去“∠”号;
(3)是一个比值 (注意比的顺序),值大于0,无单位;
(4)三角函数的大小只与∠A的大小有关,与直角三角形的边长无关.
1. ∠A的三角函数sinA、cosA和tanA
概念中的几个注意点:
概念学习
2.角相等,则对应的三角函数值相等;两锐角对应的三角函数值相等,则这两个锐角相等.
3.对于求锐角的正弦值或余弦值的问题,计算时要避免混淆“正弦”与“余弦”的概念,弄清对边、邻边与斜边的区别.
新知巩固
B
A
C
D
1.如图,∠ACB=90°,CD⊥AB,垂足为D.
(1) sinA
(2) sinB
(3) cos∠ACD
cos∠BCD
(4) tanA
tanB
CD
AB
BC
AC
AC
CD
AD
BC
CD
BC
2.求图中各直角三角形锐角的正弦、余弦值.
新知巩固
B
A
C
2
5
B1
A1
C1
6
4
sinA
cosA
sinB
cosB
sinA1
cosA1
sinB1
cosB1
例题讲解
例1 如图,在等边三角形ABC中,求cosB.
A
B
C
D
由题意知,BD=BC=AB.
在Rt△ABD中,
cosB==.
解:过点A作AD⊥BC,垂足为D.
思考:(1)在此题中,∠B等于多少度?
由此你能写出cos60°的值吗?
(2)由上图,你能求出sin60°、sin30°、cos30°的值吗?
操作与思考
怎么计算任意一个锐角的正弦、余弦值呢?
θ sin θ cos θ
15°
30°
60°
75°
0.5
0.5
0.866
0.866
如图,当一个点从原点O出发,沿着15°线移动了1个单位长度到点P时,这个点在垂直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,于是,可知sin 15°≈0. 26,cos 15°≈0. 97.
你能写出sin75°、cos75°的近似值吗?
0.26
0.97
0.97
0.26
你有何发现?
新知归纳
sinα随锐角α的增大而增大,cosα随锐角α的增大而减小.
锐角α,β sinα,sinβ cosα,cosβ
α>β
sinα>sinβ
cosαα=β
sinα=sinβ
cosα=cosβ
α<β
sinαcosα>cosβ
例题讲解
例2 用计算器求下列正弦值或余弦值(精确到0.01):
(1)sin 75°; (2)cos 75°; (3)sin 23°13'20''.
解:(1)依次按键
显示结果为0.965 925 826 3,
即sin 75°≈0.97;
(2)依次按键
即cos75°≈0.26;
显示结果为0.258 819 045 1,
(3)依次按键
即sin 23°13'20''≈0.39.
显示结果为0.394 298 367 5,
新知巩固
1. 在 Rt△ABC中,锐角 A 的对边和斜边同时扩大 100 倍,sinA 的值 ( )
A. 扩大100倍 B. 缩小 C. 不变 D. 不能确定
C
2. 下列不等式中成立的是 ( )
A. sin70°< sin60° B. cos70°< cos60°
C. tan70°< tan60° D. sin40°< sin30°
B
新知巩固
3. 梯子AB和地面所成的锐角为α,则下列说法正确的是( )
A. sinα越小,梯子越陡
B. cosα越小,梯子越陡
C. tanα越小,梯子越陡
D. α越小,梯子越陡
B
A
B
α
新知巩固
4.用计算器求下列正弦值或余弦值(精确到0.01):
(1)sin 36°; (2)cos 36°;
(3)sin 12. 5°; (4)cos 12. 5°.
解:(1)sin 36°≈0.59;
(2)cos 36°≈0.81;
(3)sin 12. 5°≈0.22;
(4)cos 12. 5°≈0.98.
新知巩固
5. 如图:在等腰△ABC中,AB=AC=5,BC=6. 求:sinB,cosB,tanB.
A
B
C
D
由题意知,BD=BC=×6=3.
在Rt△ABD中,由勾股定理得:
AD===4.
解:过点A作AD⊥BC,垂足为D.
sinB==,
cosB==,
tanB==.
课堂小结
7.2 正弦、余弦(1)
正弦、余弦的概念
利用计算器求锐角的正弦值、余弦值
正弦值、余弦值的变化规律
当堂检测
1. 如图,在△ACB中,∠C=90°,则=( )
A. sinA B. sinB C. tanA D. tanB
B
A
C
A
2.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )A. B. C. D.
当堂检测
A
α
3.如图,在△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )A. sinA= B. cosA= C. sinA= D. tanA=
当堂检测
D
A
B
C
当堂检测
5. 一等腰三角形的两边长分别为4 cm和6 cm,则其底角的余弦值为_________.
4.在Rt△ABC中,∠C=90°,AB=3,BC=1,那么∠A的正弦值是________.
6.如图,关于α与β的同一种三角函数值,有三个结论:①tanα>tanβ;②sinα>sinβ;③cosα>cosβ.
其中,正确的结论为__________.(填序号)
当堂检测
①②
α
β
当堂检测
7. 如图,在6×6正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sinA=________.
A
B
C
当堂检测
8.如图,在Rt△ABC中,∠C=90°,BC=6,tanA=. 求AB的长和sinB的值.
B
A
C
6
解:∵在Rt△ABC中,∠C=90°,BC=6,
tanA==,
∴AC=12,
∴AB===6
∴sinB===.
第7章 锐角三角函数
7.2 正弦、余弦(1)
第1课时 正弦、余弦
学习目标
1.理解并掌握正弦、余弦的概念,会在直角三角形中求一个锐角的正弦和余弦;
2.了解正弦、余弦值随锐角增大时的变化规律;
3.会用计算器求锐角的正弦值、余弦值.
实践与探索
5m
13m
如图,小红沿着某斜坡向上行走了13m,她的位置沿垂直方向上升了5m.
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
20m
?m
5m
13m
C
B
A
C1
B1
20m
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
?m
5m
13m
C
B
A
C1
B1
=
=
如果行走了am呢?
=
=
am
20m
如果小红沿着该斜坡行走了20m,那么她的位置沿垂直方向上升了多少?
实践与探索
m
5m
13m
C
B
A
C1
B1
在上述情形中,小明的位置沿水平方向又分别前进了多少?
12m
m
小红沿着斜坡行走,她的位置相对上升的高度与行走的路程有怎样的关系?
20m
思考:
讨论与交流
m
5m
13m
C
B
A
B1
她的水平方向前进的距离与行走的路程有怎样的关系?
12m
m
C1
你有何发现?
从上面的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值________;它的邻边与斜边的比值_________. (根据是_____________________)
归纳与总结
20m
m
5m
13m
C
B
A
B1
12m
m
C1
不变
不变
相似三角形的性质
概念学习
如图,在Rt△ABC中,∠C=90°,我们把∠A的对边a与斜边c的比叫做∠A的正弦(sine),记作sinA,
A
B
C
斜边c
对边a
邻边b
即 sinA==.
我们把∠A的邻边b与斜边c的比叫做∠A的余弦(cosine),
记作cosA,
即 cosA==.
你能写出∠B的正弦、余弦的表达式吗?
概念学习
在Rt△ABC中,、和的值都随∠A的大小变化而变化,都随∠A的大小确定而唯一确定. ∠A的正弦、余弦和正切都是∠A的三角函数.
A
B
C
斜边c
对边a
邻边b
三
角
函
数
正弦
正切
余弦
sinA==
cosA==
tanA==
概念中的几个注意点:
概念学习
(1)是在直角三角形中定义的,∠A是一个锐角;
(2)是一个完整的符号,习惯省去“∠”号;
(3)是一个比值 (注意比的顺序),值大于0,无单位;
(4)三角函数的大小只与∠A的大小有关,与直角三角形的边长无关.
1. ∠A的三角函数sinA、cosA和tanA
概念中的几个注意点:
概念学习
2.角相等,则对应的三角函数值相等;两锐角对应的三角函数值相等,则这两个锐角相等.
3.对于求锐角的正弦值或余弦值的问题,计算时要避免混淆“正弦”与“余弦”的概念,弄清对边、邻边与斜边的区别.
新知巩固
B
A
C
D
1.如图,∠ACB=90°,CD⊥AB,垂足为D.
(1) sinA
(2) sinB
(3) cos∠ACD
cos∠BCD
(4) tanA
tanB
CD
AB
BC
AC
AC
CD
AD
BC
CD
BC
2.求图中各直角三角形锐角的正弦、余弦值.
新知巩固
B
A
C
2
5
B1
A1
C1
6
4
sinA
cosA
sinB
cosB
sinA1
cosA1
sinB1
cosB1
例题讲解
例1 如图,在等边三角形ABC中,求cosB.
A
B
C
D
由题意知,BD=BC=AB.
在Rt△ABD中,
cosB==.
解:过点A作AD⊥BC,垂足为D.
思考:(1)在此题中,∠B等于多少度?
由此你能写出cos60°的值吗?
(2)由上图,你能求出sin60°、sin30°、cos30°的值吗?
操作与思考
怎么计算任意一个锐角的正弦、余弦值呢?
θ sin θ cos θ
15°
30°
60°
75°
0.5
0.5
0.866
0.866
如图,当一个点从原点O出发,沿着15°线移动了1个单位长度到点P时,这个点在垂直方向上升了约0.26个单位长度,在水平方向前进了约0.97个单位长度,于是,可知sin 15°≈0. 26,cos 15°≈0. 97.
你能写出sin75°、cos75°的近似值吗?
0.26
0.97
0.97
0.26
你有何发现?
新知归纳
sinα随锐角α的增大而增大,cosα随锐角α的增大而减小.
锐角α,β sinα,sinβ cosα,cosβ
α>β
sinα>sinβ
cosα
sinα=sinβ
cosα=cosβ
α<β
sinα
例题讲解
例2 用计算器求下列正弦值或余弦值(精确到0.01):
(1)sin 75°; (2)cos 75°; (3)sin 23°13'20''.
解:(1)依次按键
显示结果为0.965 925 826 3,
即sin 75°≈0.97;
(2)依次按键
即cos75°≈0.26;
显示结果为0.258 819 045 1,
(3)依次按键
即sin 23°13'20''≈0.39.
显示结果为0.394 298 367 5,
新知巩固
1. 在 Rt△ABC中,锐角 A 的对边和斜边同时扩大 100 倍,sinA 的值 ( )
A. 扩大100倍 B. 缩小 C. 不变 D. 不能确定
C
2. 下列不等式中成立的是 ( )
A. sin70°< sin60° B. cos70°< cos60°
C. tan70°< tan60° D. sin40°< sin30°
B
新知巩固
3. 梯子AB和地面所成的锐角为α,则下列说法正确的是( )
A. sinα越小,梯子越陡
B. cosα越小,梯子越陡
C. tanα越小,梯子越陡
D. α越小,梯子越陡
B
A
B
α
新知巩固
4.用计算器求下列正弦值或余弦值(精确到0.01):
(1)sin 36°; (2)cos 36°;
(3)sin 12. 5°; (4)cos 12. 5°.
解:(1)sin 36°≈0.59;
(2)cos 36°≈0.81;
(3)sin 12. 5°≈0.22;
(4)cos 12. 5°≈0.98.
新知巩固
5. 如图:在等腰△ABC中,AB=AC=5,BC=6. 求:sinB,cosB,tanB.
A
B
C
D
由题意知,BD=BC=×6=3.
在Rt△ABD中,由勾股定理得:
AD===4.
解:过点A作AD⊥BC,垂足为D.
sinB==,
cosB==,
tanB==.
课堂小结
7.2 正弦、余弦(1)
正弦、余弦的概念
利用计算器求锐角的正弦值、余弦值
正弦值、余弦值的变化规律
当堂检测
1. 如图,在△ACB中,∠C=90°,则=( )
A. sinA B. sinB C. tanA D. tanB
B
A
C
A
2.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )A. B. C. D.
当堂检测
A
α
3.如图,在△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )A. sinA= B. cosA= C. sinA= D. tanA=
当堂检测
D
A
B
C
当堂检测
5. 一等腰三角形的两边长分别为4 cm和6 cm,则其底角的余弦值为_________.
4.在Rt△ABC中,∠C=90°,AB=3,BC=1,那么∠A的正弦值是________.
6.如图,关于α与β的同一种三角函数值,有三个结论:①tanα>tanβ;②sinα>sinβ;③cosα>cosβ.
其中,正确的结论为__________.(填序号)
当堂检测
①②
α
β
当堂检测
7. 如图,在6×6正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sinA=________.
A
B
C
当堂检测
8.如图,在Rt△ABC中,∠C=90°,BC=6,tanA=. 求AB的长和sinB的值.
B
A
C
6
解:∵在Rt△ABC中,∠C=90°,BC=6,
tanA==,
∴AC=12,
∴AB===6
∴sinB===.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
