7.5 解直角三角形(第2课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 7.5 解直角三角形(第2课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:33:10 | ||
图片预览







文档简介
(共31张PPT)
第7章 锐角三角函数
7.5 解直角三角形(2)
第2课时 构造直角三角形解题
学习目标
1. 会解含特殊角的非直角三角形;
2. 会利用解直角三角形求解能化为直角三角形的简单多边形问题.
知识回顾
1. 什么叫解直角三角形?
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
2. 直角三角形中需要知道其中的几个元素就可以确定这个直角三角形的形状和大小?对于已知的元素有限制吗?
除直角外需要知道两个元素(其中至少有一个是边).
问题情境
如图,平顶屋面(截面为等腰三角形)的宽度为l,坡顶的高度为h,
(2)若已知宽度l和坡顶的倾角α , 你能求出斜面钢条的长度和坡顶的高度 h吗?
α
h
l
(1)你能求出斜面钢条的长度和倾角α吗?
A
C
B
D
h
A
B
D
α
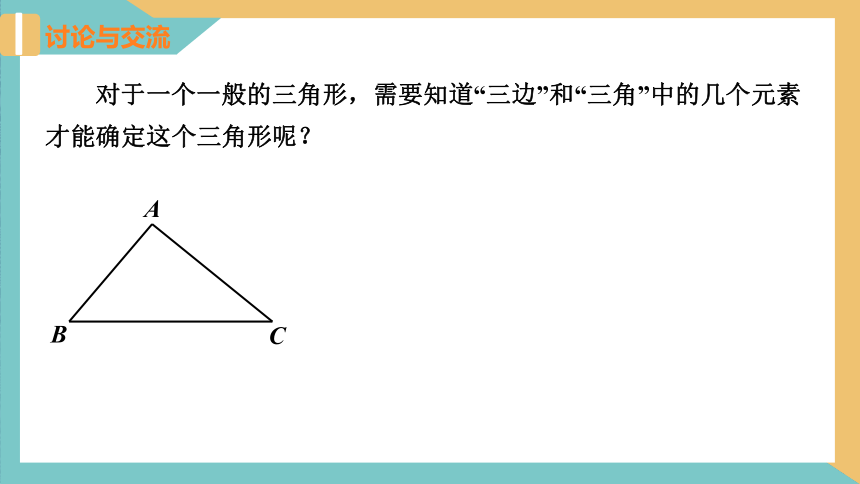
对于一个一般的三角形,需要知道“三边”和“三角”中的几个元素才能确定这个三角形呢?
讨论与交流
C
B
A
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
D
30°
45°
构造直角三角形
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°=,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=4,
∴AB=AD+DB=+4.
例题讲解
变式1 如图,已知 AC = 8,∠A=30°,tanB=,求 AB 的长.
A
B
C
D
30°
在Rt△CDB中,
解:如图,作CD⊥AB于点D,
在Rt△ACD中,
∵ tanB= ,
∴ BD= = .
AD=AC cos30°=,
CD=AC sin30°==4,
∴ AB=AD+DB=+.
例题讲解
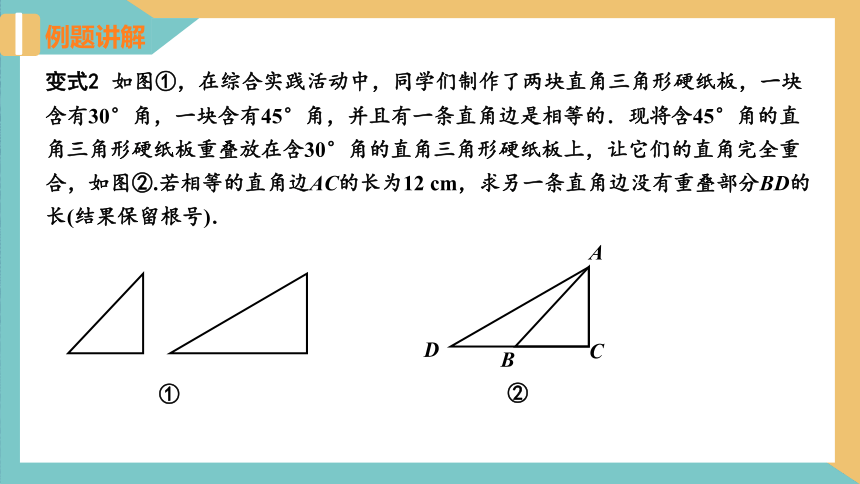
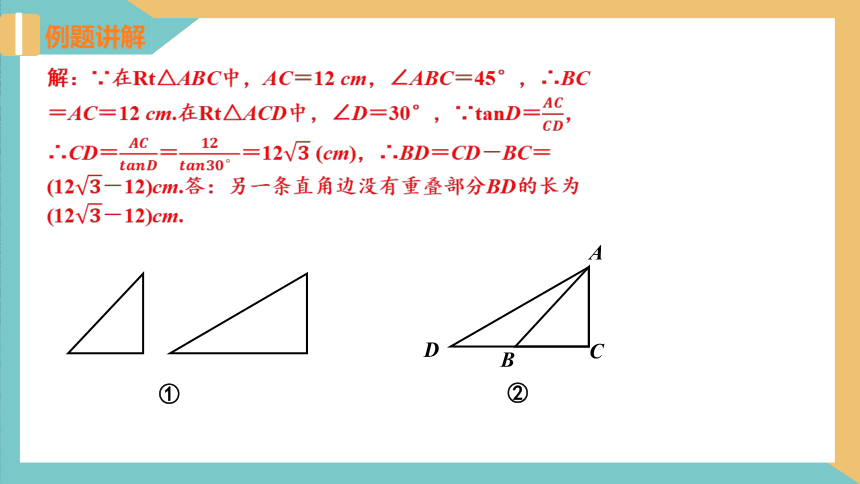
变式2 如图①,在综合实践活动中,同学们制作了两块直角三角形硬纸板,一块含有30°角,一块含有45°角,并且有一条直角边是相等的.现将含45°角的直角三角形硬纸板重叠放在含30°角的直角三角形硬纸板上,让它们的直角完全重合,如图②.若相等的直角边AC的长为12 cm,求另一条直角边没有重叠部分BD的长(结果保留根号).
①
②
A
B
C
D
例题讲解
解:∵在Rt△ABC中,AC=12 cm,∠ABC=45°,∴BC=AC=12 cm.在Rt△ACD中,∠D=30°,∵tanD=,∴CD===12 (cm),∴BD=CD-BC=(12-12)cm.答:另一条直角边没有重叠部分BD的长为(12-12)cm.
①
②
A
B
C
D
例题讲解
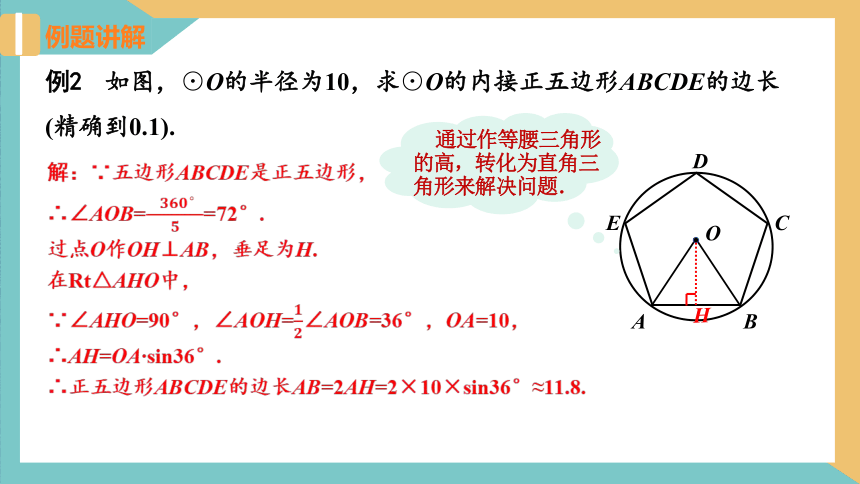
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
D
E
A
B
C
O
H
解:∵五边形ABCDE是正五边形,
∴∠AOB==72°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=36°,OA=10,
∴AH=OA sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
通过作等腰三角形的高,转化为直角三角形来解决问题.
例题讲解
D
E
A
B
C
O
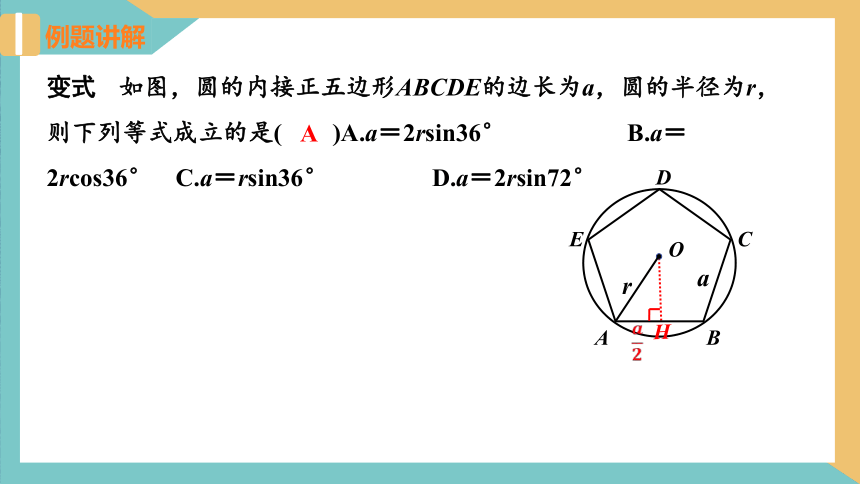
变式 如图,圆的内接正五边形ABCDE的边长为a,圆的半径为r,则下列等式成立的是( )A.a=2rsin36° B.a=2rcos36° C.a=rsin36° D.a=2rsin72°
a
r
H
A
例3 ABCD中,∠A=60°,AB=8,AD=6,求 ABCD的面积.
A
B
C
D
6
60°
8
E
解:过点D作DE⊥AB,垂足为E.
在Rt△ADE中,
∵∠AED=90°,∠A=60°,AD=6,
∴DE=AD sinA=6×sin60°=.
∴S ABCD=AB×DE=8×=24.
例题讲解
新知巩固
1. 如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为
________.
B
C
A
D
3
1
新知巩固
2. 求半径为12的圆的内接正八边形的边长(精确到0.1).
A
B
O
H
解:∵八边形ABCDEFGH是正八边形,
∴∠AOB==45°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=22.5°,OA=12,
∴AH=OA sin22.5°=12sin22.5°.
∴正五边形ABCDE的边长AB=2AH=2×12×sin22.5°≈9.2.
C
D
E
F
G
H
新知巩固
3. 如图,在菱形钢架ABCD中,AB=2m,∠BAD=72°,焊接这个钢架约需多长的钢材(精确到0.1m)
解:∵四边形ABCD是菱形,
∴ AC⊥BD, OA= OC,OB=OD,
∠BAO=∠BAD=36°,
∴OB= AB· sin 36°,OA=AB· cos 36°.
∴焊接这个钢架的长度
=4AB+ABsin 36°+ABcos 36°
=4×2+2×1.18+2×1.62
≈ 13.6(m)
O
1. 对于非直角三角形问题,往往通过图形的高或作一边上的____,构造______三角形.
归纳总结
高
直角
2.对于正n边形问题,往往作出这个正n边形的外接圆半径和内切圆半径,使得问题化归到_____三角形中,且这个三角形两边(外接圆半径和内切圆半径)的夹角为________度,再运用条件解决问题.
直角
一般情况下是从非特殊角的顶点作高, 这样有利于计算.
课堂小结
7.5 解直角三角形(2)
含特殊角的非直角三角形
正n边形问题
能化为直角三角形的简单多边形问题
当堂检测
1.如图,在△ABC中,AB=AC,AD⊥BC于点D.若BC=24,cosB=,则AD的长为( )
A. 12 B.10 C. 6 D. 5
D
A
C
B
D
当堂检测
2. 如图,在△ABC中,∠B=45°,∠C=30°,若AB=2,则AC的长为 ( )A. 3 B. 4 C. 2 D. 2
C
C
B
A
当堂检测
3. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4, sinB=,则菱形的周长是( )
A.10 B.20 C.40 D.28
C
B
C
D
A
E
当堂检测
4. 2000年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的外接圆的半径是R,那么它的边长是( )A. Rsin20° B. Rsin40° C. 2Rsin20° D.2 Rsin40°
C
当堂检测
5. 如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为( )A. B.
C.1 D.2
B
当堂检测
6.如图,在△ABC中,AD⊥BC于点D,AD=2,∠B=30°,S△ABC=10,则tanC的值为_________.
B
C
A
D
C
A
D
当堂检测
7. 在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于________.
8. 等腰三角形的周长为2+,腰长为1,则底角等于_________.
30°
当堂检测
9. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
B
C
A
D
当堂检测
10. 如图,在平行四边形ABCD中,对角线AC,BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是_______.
12
B
C
D
A
O
α
E
当堂检测
11. 如图,△ABC内接于⊙O,AO=2,BC=2,则∠BAC的度数为________.
A
C
B
D
O
●
2
2
60°
当堂检测
12. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
当堂检测
13. 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD===5.
当△ABC为锐角三角形时,如图①,
BC=BD+CD=12+5=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
当堂检测
14.如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,
求此四边形ABCD的面积.
A
B
C
D
2
60°
1
E
解:如图,延长BC、AD交于点E.∵∠B=90°,∠A=60°,∴∠E=30°.在Rt△ABE中,
AE=2AB=4,BE=AE·cos30°=2 .在Rt△ECD中,
EC=2CD=2,DE=EC·cos30°=,∴SRt△ABE=AB·BE=×2×2=2,SRt△ECD=CD·DE=×1×=,∴S四边形ABCD=SRt△ABE-SRt△ECD=2-=.
F
思维提升
你能根据图上信息,提出一个用锐角三角函数解决的实际问题吗?试一试.
400米
P
B
C
A
30°
45°
第7章 锐角三角函数
7.5 解直角三角形(2)
第2课时 构造直角三角形解题
学习目标
1. 会解含特殊角的非直角三角形;
2. 会利用解直角三角形求解能化为直角三角形的简单多边形问题.
知识回顾
1. 什么叫解直角三角形?
由直角三角形的边、角中的已知元素,求出所有边、角中的未知元素的过程,叫做解直角三角形.
2. 直角三角形中需要知道其中的几个元素就可以确定这个直角三角形的形状和大小?对于已知的元素有限制吗?
除直角外需要知道两个元素(其中至少有一个是边).
问题情境
如图,平顶屋面(截面为等腰三角形)的宽度为l,坡顶的高度为h,
(2)若已知宽度l和坡顶的倾角α , 你能求出斜面钢条的长度和坡顶的高度 h吗?
α
h
l
(1)你能求出斜面钢条的长度和倾角α吗?
A
C
B
D
h
A
B
D
α
对于一个一般的三角形,需要知道“三边”和“三角”中的几个元素才能确定这个三角形呢?
讨论与交流
C
B
A
例题讲解
例1 如图,在△ABC中,AC=8,∠B=45°,∠A=30°,求AB.
A
B
C
D
30°
45°
构造直角三角形
解:过点C作CD⊥AB,垂足为D.
在Rt△ADC中,
AD=AC cos30°=,
CD=AC sin30°==4,
在Rt△BCD中,
∵∠B=45°,
∴BD=CD=4,
∴AB=AD+DB=+4.
例题讲解
变式1 如图,已知 AC = 8,∠A=30°,tanB=,求 AB 的长.
A
B
C
D
30°
在Rt△CDB中,
解:如图,作CD⊥AB于点D,
在Rt△ACD中,
∵ tanB= ,
∴ BD= = .
AD=AC cos30°=,
CD=AC sin30°==4,
∴ AB=AD+DB=+.
例题讲解
变式2 如图①,在综合实践活动中,同学们制作了两块直角三角形硬纸板,一块含有30°角,一块含有45°角,并且有一条直角边是相等的.现将含45°角的直角三角形硬纸板重叠放在含30°角的直角三角形硬纸板上,让它们的直角完全重合,如图②.若相等的直角边AC的长为12 cm,求另一条直角边没有重叠部分BD的长(结果保留根号).
①
②
A
B
C
D
例题讲解
解:∵在Rt△ABC中,AC=12 cm,∠ABC=45°,∴BC=AC=12 cm.在Rt△ACD中,∠D=30°,∵tanD=,∴CD===12 (cm),∴BD=CD-BC=(12-12)cm.答:另一条直角边没有重叠部分BD的长为(12-12)cm.
①
②
A
B
C
D
例题讲解
例2 如图,⊙O的半径为10,求⊙O的内接正五边形ABCDE的边长
(精确到0.1).
D
E
A
B
C
O
H
解:∵五边形ABCDE是正五边形,
∴∠AOB==72°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=36°,OA=10,
∴AH=OA sin36°.
∴正五边形ABCDE的边长AB=2AH=2×10×sin36°≈11.8.
通过作等腰三角形的高,转化为直角三角形来解决问题.
例题讲解
D
E
A
B
C
O
变式 如图,圆的内接正五边形ABCDE的边长为a,圆的半径为r,则下列等式成立的是( )A.a=2rsin36° B.a=2rcos36° C.a=rsin36° D.a=2rsin72°
a
r
H
A
例3 ABCD中,∠A=60°,AB=8,AD=6,求 ABCD的面积.
A
B
C
D
6
60°
8
E
解:过点D作DE⊥AB,垂足为E.
在Rt△ADE中,
∵∠AED=90°,∠A=60°,AD=6,
∴DE=AD sinA=6×sin60°=.
∴S ABCD=AB×DE=8×=24.
例题讲解
新知巩固
1. 如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为
________.
B
C
A
D
3
1
新知巩固
2. 求半径为12的圆的内接正八边形的边长(精确到0.1).
A
B
O
H
解:∵八边形ABCDEFGH是正八边形,
∴∠AOB==45°.
过点O作OH⊥AB,垂足为H.
在Rt△AHO中,
∵∠AHO=90°,∠AOH=∠AOB=22.5°,OA=12,
∴AH=OA sin22.5°=12sin22.5°.
∴正五边形ABCDE的边长AB=2AH=2×12×sin22.5°≈9.2.
C
D
E
F
G
H
新知巩固
3. 如图,在菱形钢架ABCD中,AB=2m,∠BAD=72°,焊接这个钢架约需多长的钢材(精确到0.1m)
解:∵四边形ABCD是菱形,
∴ AC⊥BD, OA= OC,OB=OD,
∠BAO=∠BAD=36°,
∴OB= AB· sin 36°,OA=AB· cos 36°.
∴焊接这个钢架的长度
=4AB+ABsin 36°+ABcos 36°
=4×2+2×1.18+2×1.62
≈ 13.6(m)
O
1. 对于非直角三角形问题,往往通过图形的高或作一边上的____,构造______三角形.
归纳总结
高
直角
2.对于正n边形问题,往往作出这个正n边形的外接圆半径和内切圆半径,使得问题化归到_____三角形中,且这个三角形两边(外接圆半径和内切圆半径)的夹角为________度,再运用条件解决问题.
直角
一般情况下是从非特殊角的顶点作高, 这样有利于计算.
课堂小结
7.5 解直角三角形(2)
含特殊角的非直角三角形
正n边形问题
能化为直角三角形的简单多边形问题
当堂检测
1.如图,在△ABC中,AB=AC,AD⊥BC于点D.若BC=24,cosB=,则AD的长为( )
A. 12 B.10 C. 6 D. 5
D
A
C
B
D
当堂检测
2. 如图,在△ABC中,∠B=45°,∠C=30°,若AB=2,则AC的长为 ( )A. 3 B. 4 C. 2 D. 2
C
C
B
A
当堂检测
3. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4, sinB=,则菱形的周长是( )
A.10 B.20 C.40 D.28
C
B
C
D
A
E
当堂检测
4. 2000年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的外接圆的半径是R,那么它的边长是( )A. Rsin20° B. Rsin40° C. 2Rsin20° D.2 Rsin40°
C
当堂检测
5. 如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=30°,则点B到OC的距离为( )A. B.
C.1 D.2
B
当堂检测
6.如图,在△ABC中,AD⊥BC于点D,AD=2,∠B=30°,S△ABC=10,则tanC的值为_________.
B
C
A
D
C
A
D
当堂检测
7. 在Rt△ABC中,∠C=90°,若AB=4,sinA=,则斜边上的高等于________.
8. 等腰三角形的周长为2+,腰长为1,则底角等于_________.
30°
当堂检测
9. 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
B
C
A
D
当堂检测
10. 如图,在平行四边形ABCD中,对角线AC,BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是_______.
12
B
C
D
A
O
α
E
当堂检测
11. 如图,△ABC内接于⊙O,AO=2,BC=2,则∠BAC的度数为________.
A
C
B
D
O
●
2
2
60°
当堂检测
12. 求半径为20的圆的内接正三角形的边长和面积(精确到0.1).
A
C
B
●
O
H
解:∵△ABC是正三角形,
∴∠BOC==120°.
过点O作OH⊥BC,垂足为H.
在Rt△BOH中,
∵∠BHO=90°,∠BOH=∠BOC=60°,OB=20,
∴BH=OB sin60°,OH=OB cos60°.
∴△ABC的边长BC=2BH=2×20×sin60°≈34.6.
S△ABC=3××BC×OH=×40×sin60°×20cos60°=519.6.
当堂检测
13. 在△ABC中,AB=12,AC=13,cosB=,求BC的长.
A
C
B
A
C
B
①
②
D
D
解:∵AB=12,∠B=45°,
∴AD=BD=ABcosB=12×=12,
在Rt△ACD中,由勾股定理得,
CD===5.
当△ABC为锐角三角形时,如图①,
BC=BD+CD=12+5=17.
当△ABC为钝角三角形时,如图②,
BC=BD-CD=12-5=7.
当堂检测
14.如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,
求此四边形ABCD的面积.
A
B
C
D
2
60°
1
E
解:如图,延长BC、AD交于点E.∵∠B=90°,∠A=60°,∴∠E=30°.在Rt△ABE中,
AE=2AB=4,BE=AE·cos30°=2 .在Rt△ECD中,
EC=2CD=2,DE=EC·cos30°=,∴SRt△ABE=AB·BE=×2×2=2,SRt△ECD=CD·DE=×1×=,∴S四边形ABCD=SRt△ABE-SRt△ECD=2-=.
F
思维提升
你能根据图上信息,提出一个用锐角三角函数解决的实际问题吗?试一试.
400米
P
B
C
A
30°
45°
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
