7.6 用锐角三角函数解决问题(第2课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版)
文档属性
| 名称 | 7.6 用锐角三角函数解决问题(第2课时)(课件)-2023-2024学年九年级数学下册同步精品课件(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:36:06 | ||
图片预览







文档简介
(共26张PPT)
第7章 锐角三角函数
7.6 用锐角三角函数解决问题(2)
第2课时 与圆有关的问题
学习目标
进一步掌握锐角三角函数的简单应用,能利用解直角三角形的知识解决与圆有关的实际问题.
问题情境
五一期间,小明和同学一起到游乐场玩.
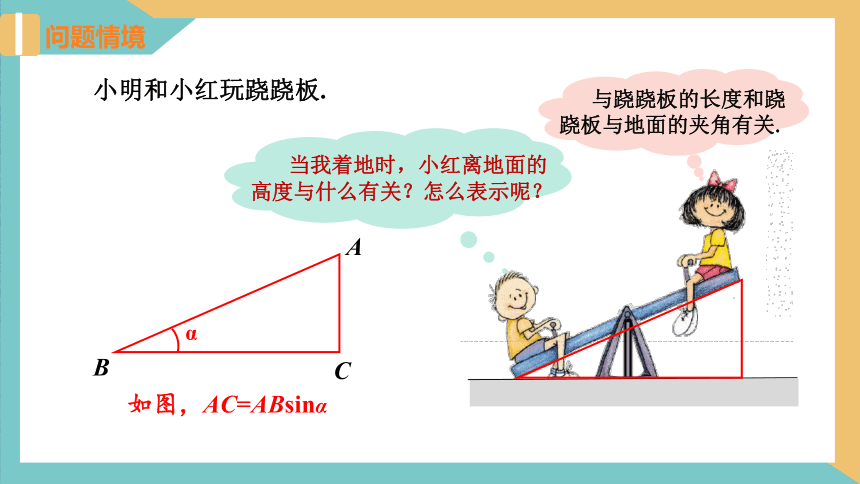
小明和小红玩跷跷板.
如图,AC=ABsinα
A
B
C
α
当我着地时,小红离地面的高度与什么有关?怎么表示呢?
与跷跷板的长度和跷跷板与地面的夹角有关.
问题情境
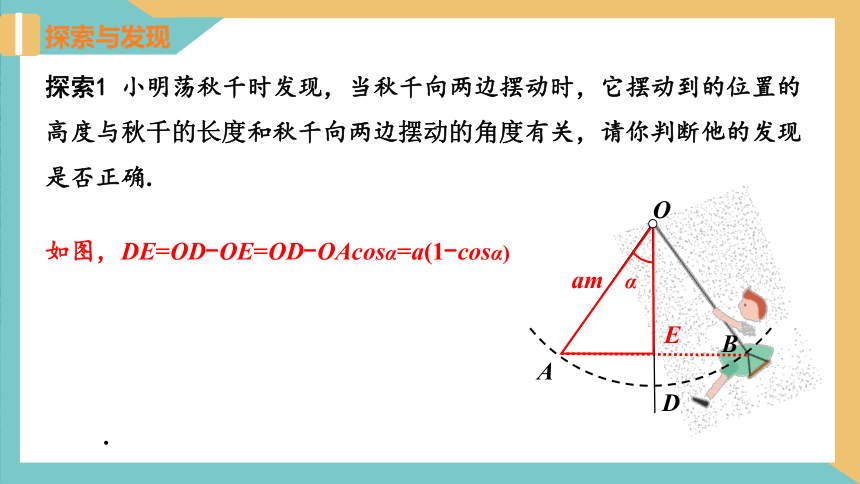
探索1 小明荡秋千时发现,当秋千向两边摆动时,它摆动到的位置的高度与秋千的长度和秋千向两边摆动的角度有关,请你判断他的发现是否正确.
α
B
O
A
E
am
D
探索与发现
.
如图,DE=OD-OE=OD-OAcosα=a(1-cosα)
探索2 小明坐上摩天轮,从底部出发开始观光.摩天轮的半径为20m,底部与地面相距0.3m,旋转1周需要12min.经过多长时间小明到达最高点?此时离地面多高?
探索与发现
20m
0.3m
A
D
O
B
如图,用⊙O表示摩天轮,A、B分别表示小
明出发点和出发后的到达点.
由题意知,OB=OA=20,AD=0.3m,
小明离地面的最高点的距离=20×2+0.3=40.3m.
因为旋转1周需要12min,所以小明到达最
高点需要6min.
解:如图,用⊙O表示摩天轮,A、B分别表示小明出
发点和2min后的到达点. 由题意知,OB=20.
∵旋转1周用时12 min,
∴2 min后∠BOA的度数为==60°,
过点B作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB cos∠BOC=20×cos60°=20×=10,
AC=AO-CO=20-10=10.
∵AD=0.3m,
∴小明离地面的高度=10+0.3=10.3m.
答:2min后小明离地面10.3m.
爱动脑筋的小红问:2 min后,小明离地面多高?
探索与发现
C
20m
0.3m
A
D
O
B
解:如图,用⊙O表示摩天轮,A、B分别表示小明出
发点和5min后的到达点. 由题意知,OB=20.
∵旋转1周用时12 min,
∴5 min后∠BOA的度数为==150°
∴∠BOE=30°
过点B作BC⊥OE,垂足为C.
在Rt△OCB中,
OC=OB cos∠BOC=20×cos30°=20×=10,
AC=AO+CO=20+10.
∵AD=0.3m,∴小明离地面的高度=20+10+0.3≈37.6m.
答:5min后小明离地面37.6m.
20m
0.3m
变式1 5 min后,小明离地面多高?(精确到0.1 m)
B
E
C
A
D
O
拓展与延伸
A
D
O
B
变式2 摩天轮转动多长时间后,小明离地面的高度将首次达到15.3m
拓展与延伸
C
20m
0.3m
θ
解:如图,设旋转角为θ,
∵15.3<20.3,
∴根据题意,得
cosθ===,
用计算器计算,得θ≈75.5°.
∴≈2.52min.
答:摩天轮转动约2.52min后,小明离地面的高度将首次达到15.3m.
变式3 摩天轮转动1周,小明在离地面30.3m以上的空中有多长时间
拓展与延伸
解:如图,设旋转角为180°-θ,
∵30.3>20.3,
∴根据题意,得
cosθ===,
∴θ=60°.
=4min.
12-4×2=4min.
答:小明在离地面30.3m以上的空中4min.
20m
0.3m
B
E
C
A
D
O
θ
归纳总结
2. 根据实际问题构造出直角三角形,确定直角三角形中的已知元素和未知元素,从而选择适当的三角函数的关系式.
1. 一个圆绕圆心旋转1周需要m min,那么旋转n min(n≤m)后的旋转角(圆心角)的度数是________.
1. 如图,钟摆的摆长AB为90cm,当它摆动到AB'的位置时∠BAB′=11°,这时摆球B'相对于最低点B升高了多少 (精确到1cm)
A
B
B′
C
新知巩固
解:根据题意,得
cos∠CAB′=,
AC=AB′cos∠CAB′=90cos11°=88.3.
BC=AB-AC=90-88.3=1.7≈2cm.
答:这时摆球B'相对于最低点B升高了2cm.
2. 已知跷跷板长4m,当跷跷板的一端碰到地面时,另一端离地面1.5m.求此时跷跷板与地面的夹角(精确到0.1°).
A
B
O
C
4m
1.5m
解:如图,AB=4m,AC=1.5m
sin∠BAC===0.375,
由计算器计算得,
∠BAC≈22.0°.
答:此时跷跷板与地面的夹角为22.0°.
新知巩固
新知巩固
3. 如图,在欢乐谷中有一座直径为120 m的摩天轮,旋转1周用时30 min.小明从摩天轮的底部(与地面相距0.5 m)出发开始观光.(1)10 min后小明离地面多高?
0.5m
B
A
O
C
H
G
解:∵旋转1周用时30 min,
∴10min后∠BOC的度数为==120°,
∴∠COG=60°
过点C作CH⊥OG,垂足为H.
在Rt△COH中,OC=60.
OH=OC cos∠COH=60×cos60°=60×=30.
AH=AB+BO+OH=0.5+60+30=90.5 .
答:10min后小明离地面90.5m.
60m
新知巩固
(2)摩天轮转动1周,小明在(1)中所求的高度以上,会持续多长时间?
0.5m
B
A
O
C
H
G
60m
解:(2)由(1)得10 min到达C的高度,
由对称性可得持续多长时间为
30-10×2=10min.
答:小明在(1)中所求的高度以上,会持续的时间为10min.
课堂小结
7.6 用锐角三角函数解决问题(2)
构造合适的直角三角形
选择适当的三角函数关系式
当堂检测
1.如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6 m,则OC的长为( )
A. 0.8cos20°m B. 0.8sin20° m C. m D. m
B
A
M
O
B
C
N
当堂检测
2.如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为a,一辆小汽车车门宽AO为b,当车门打开角度∠AOB为α时,车门边缘的点A处与墙的距离为( )A. a-bsinα B. a-btanα C. a- D. a-
A
当堂检测
3.如图,一块直角三角板和一张光盘竖放在桌面上,其中A是光盘与桌面的切点,∠BAC=60°,光盘的直径是80 cm,则三角板的斜边AB被光盘截得的线段AD的长为( )A. 20 cm B. 40 cmC. 80 cm D. 80 cm
B
当堂检测
4. 如图,秋千吊绳的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为____m.
(结果保留根号)
0.5m
3m
60°
2
当堂检测
5. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了_________.
2米
α
A
B
β
当堂检测
6. 已知一个不等臂跷跷板AB长4米,支撑柱OH垂直地面,如图①,当AB的一端A着地时,AB与地面夹角的正弦值为;如图②,当AB的另一端B着地时,AB与地面夹角的正弦值为,则支撑柱OH的长为________.
0.8米
A
B
A
B
H
H
O
O
①
②
当堂检测
7. “十一”假期,小明和同学一起到游乐场游玩,如图,游乐场的大型摩天轮的半径为15 m,旋转1周需要24 min(匀速).小明乘坐最底部(离地面约1 m)的车厢按逆时针方向旋转开始1周的观光,启动4 min时,小明离地面的高度是________m.
8.5
A
O
当堂检测
8.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
当堂检测
问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.
问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;
解:由于筒车每旋转一周用时120秒,
所以每秒转过360°÷120=3°,
∴∠BOM=360°-3°×95-30°=45°.
当堂检测
(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)
解:如图,分别过点B,A作OM的垂线,垂足为C,D.在Rt△AOD中,∠AOD=30°,OA=2米,∴OD=OA=米.
在Rt△BOC中,∠BOC=45°,OB=2米,∴OC=OB=米,∴CD=OD-OC=-≈0.3(米).
答:该盛水筒旋转至B处时到水面的距离约为0.3米.
第7章 锐角三角函数
7.6 用锐角三角函数解决问题(2)
第2课时 与圆有关的问题
学习目标
进一步掌握锐角三角函数的简单应用,能利用解直角三角形的知识解决与圆有关的实际问题.
问题情境
五一期间,小明和同学一起到游乐场玩.
小明和小红玩跷跷板.
如图,AC=ABsinα
A
B
C
α
当我着地时,小红离地面的高度与什么有关?怎么表示呢?
与跷跷板的长度和跷跷板与地面的夹角有关.
问题情境
探索1 小明荡秋千时发现,当秋千向两边摆动时,它摆动到的位置的高度与秋千的长度和秋千向两边摆动的角度有关,请你判断他的发现是否正确.
α
B
O
A
E
am
D
探索与发现
.
如图,DE=OD-OE=OD-OAcosα=a(1-cosα)
探索2 小明坐上摩天轮,从底部出发开始观光.摩天轮的半径为20m,底部与地面相距0.3m,旋转1周需要12min.经过多长时间小明到达最高点?此时离地面多高?
探索与发现
20m
0.3m
A
D
O
B
如图,用⊙O表示摩天轮,A、B分别表示小
明出发点和出发后的到达点.
由题意知,OB=OA=20,AD=0.3m,
小明离地面的最高点的距离=20×2+0.3=40.3m.
因为旋转1周需要12min,所以小明到达最
高点需要6min.
解:如图,用⊙O表示摩天轮,A、B分别表示小明出
发点和2min后的到达点. 由题意知,OB=20.
∵旋转1周用时12 min,
∴2 min后∠BOA的度数为==60°,
过点B作BC⊥OA,垂足为C.
在Rt△OCB中,
OC=OB cos∠BOC=20×cos60°=20×=10,
AC=AO-CO=20-10=10.
∵AD=0.3m,
∴小明离地面的高度=10+0.3=10.3m.
答:2min后小明离地面10.3m.
爱动脑筋的小红问:2 min后,小明离地面多高?
探索与发现
C
20m
0.3m
A
D
O
B
解:如图,用⊙O表示摩天轮,A、B分别表示小明出
发点和5min后的到达点. 由题意知,OB=20.
∵旋转1周用时12 min,
∴5 min后∠BOA的度数为==150°
∴∠BOE=30°
过点B作BC⊥OE,垂足为C.
在Rt△OCB中,
OC=OB cos∠BOC=20×cos30°=20×=10,
AC=AO+CO=20+10.
∵AD=0.3m,∴小明离地面的高度=20+10+0.3≈37.6m.
答:5min后小明离地面37.6m.
20m
0.3m
变式1 5 min后,小明离地面多高?(精确到0.1 m)
B
E
C
A
D
O
拓展与延伸
A
D
O
B
变式2 摩天轮转动多长时间后,小明离地面的高度将首次达到15.3m
拓展与延伸
C
20m
0.3m
θ
解:如图,设旋转角为θ,
∵15.3<20.3,
∴根据题意,得
cosθ===,
用计算器计算,得θ≈75.5°.
∴≈2.52min.
答:摩天轮转动约2.52min后,小明离地面的高度将首次达到15.3m.
变式3 摩天轮转动1周,小明在离地面30.3m以上的空中有多长时间
拓展与延伸
解:如图,设旋转角为180°-θ,
∵30.3>20.3,
∴根据题意,得
cosθ===,
∴θ=60°.
=4min.
12-4×2=4min.
答:小明在离地面30.3m以上的空中4min.
20m
0.3m
B
E
C
A
D
O
θ
归纳总结
2. 根据实际问题构造出直角三角形,确定直角三角形中的已知元素和未知元素,从而选择适当的三角函数的关系式.
1. 一个圆绕圆心旋转1周需要m min,那么旋转n min(n≤m)后的旋转角(圆心角)的度数是________.
1. 如图,钟摆的摆长AB为90cm,当它摆动到AB'的位置时∠BAB′=11°,这时摆球B'相对于最低点B升高了多少 (精确到1cm)
A
B
B′
C
新知巩固
解:根据题意,得
cos∠CAB′=,
AC=AB′cos∠CAB′=90cos11°=88.3.
BC=AB-AC=90-88.3=1.7≈2cm.
答:这时摆球B'相对于最低点B升高了2cm.
2. 已知跷跷板长4m,当跷跷板的一端碰到地面时,另一端离地面1.5m.求此时跷跷板与地面的夹角(精确到0.1°).
A
B
O
C
4m
1.5m
解:如图,AB=4m,AC=1.5m
sin∠BAC===0.375,
由计算器计算得,
∠BAC≈22.0°.
答:此时跷跷板与地面的夹角为22.0°.
新知巩固
新知巩固
3. 如图,在欢乐谷中有一座直径为120 m的摩天轮,旋转1周用时30 min.小明从摩天轮的底部(与地面相距0.5 m)出发开始观光.(1)10 min后小明离地面多高?
0.5m
B
A
O
C
H
G
解:∵旋转1周用时30 min,
∴10min后∠BOC的度数为==120°,
∴∠COG=60°
过点C作CH⊥OG,垂足为H.
在Rt△COH中,OC=60.
OH=OC cos∠COH=60×cos60°=60×=30.
AH=AB+BO+OH=0.5+60+30=90.5 .
答:10min后小明离地面90.5m.
60m
新知巩固
(2)摩天轮转动1周,小明在(1)中所求的高度以上,会持续多长时间?
0.5m
B
A
O
C
H
G
60m
解:(2)由(1)得10 min到达C的高度,
由对称性可得持续多长时间为
30-10×2=10min.
答:小明在(1)中所求的高度以上,会持续的时间为10min.
课堂小结
7.6 用锐角三角函数解决问题(2)
构造合适的直角三角形
选择适当的三角函数关系式
当堂检测
1.如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6 m,则OC的长为( )
A. 0.8cos20°m B. 0.8sin20° m C. m D. m
B
A
M
O
B
C
N
当堂检测
2.如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为a,一辆小汽车车门宽AO为b,当车门打开角度∠AOB为α时,车门边缘的点A处与墙的距离为( )A. a-bsinα B. a-btanα C. a- D. a-
A
当堂检测
3.如图,一块直角三角板和一张光盘竖放在桌面上,其中A是光盘与桌面的切点,∠BAC=60°,光盘的直径是80 cm,则三角板的斜边AB被光盘截得的线段AD的长为( )A. 20 cm B. 40 cmC. 80 cm D. 80 cm
B
当堂检测
4. 如图,秋千吊绳的长度为3 m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为____m.
(结果保留根号)
0.5m
3m
60°
2
当堂检测
5. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了_________.
2米
α
A
B
β
当堂检测
6. 已知一个不等臂跷跷板AB长4米,支撑柱OH垂直地面,如图①,当AB的一端A着地时,AB与地面夹角的正弦值为;如图②,当AB的另一端B着地时,AB与地面夹角的正弦值为,则支撑柱OH的长为________.
0.8米
A
B
A
B
H
H
O
O
①
②
当堂检测
7. “十一”假期,小明和同学一起到游乐场游玩,如图,游乐场的大型摩天轮的半径为15 m,旋转1周需要24 min(匀速).小明乘坐最底部(离地面约1 m)的车厢按逆时针方向旋转开始1周的观光,启动4 min时,小明离地面的高度是________m.
8.5
A
O
当堂检测
8.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
当堂检测
问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.
问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;
解:由于筒车每旋转一周用时120秒,
所以每秒转过360°÷120=3°,
∴∠BOM=360°-3°×95-30°=45°.
当堂检测
(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)
解:如图,分别过点B,A作OM的垂线,垂足为C,D.在Rt△AOD中,∠AOD=30°,OA=2米,∴OD=OA=米.
在Rt△BOC中,∠BOC=45°,OB=2米,∴OC=OB=米,∴CD=OD-OC=-≈0.3(米).
答:该盛水筒旋转至B处时到水面的距离约为0.3米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
