8.2.2 二元一次方程组的解法---加减消元法(第二课时) 课件(共27张PPT)
文档属性
| 名称 | 8.2.2 二元一次方程组的解法---加减消元法(第二课时) 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 13:27:25 | ||
图片预览




文档简介
(共27张PPT)
第8章 二元一次方程组
8.2.1 二元一次方程组的解法
(代入消元法)
第四单元
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组. (重点、难点)
1.把下列方程写成用含x的式子表示y的形式.
(1) 2x+y=6
(2) y-3x-1=0
2.你能把上面两个方程写成用含y的式子表示x的形式.
3.如何解这样的方程组 .
y=6-2x
y=3x+1
(1)
(2)
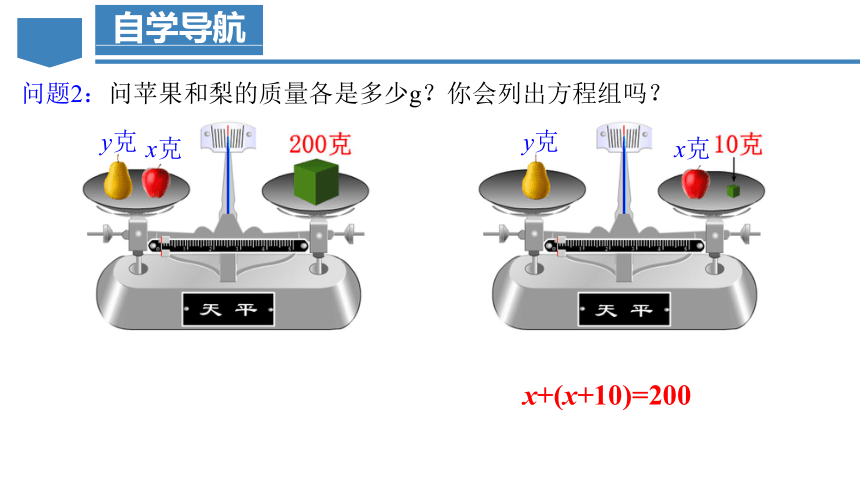
一个苹果和一个梨的质量合计200g;
这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等.
问题1:观察下面两个天平你能从中得到哪些信息?
问题2:问苹果和梨的质量各是多少g?你会列出方程组吗?
x克
y克
x克
y克
x+(x+10)=200
问题2:问苹果和梨的质量各是多少g?你会列出方程组吗?
x克
y克
x克
y克
x+(x+10)=200
①②
y
转化
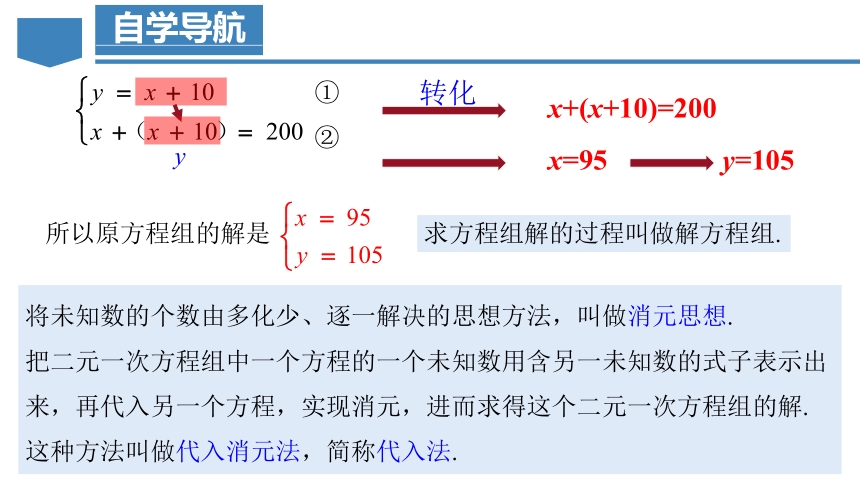
x+(x+10)=200
①②
y
转化
x=95
y=105
所以原方程组的解是
求方程组解的过程叫做解方程组.
将未知数的个数由多化少、逐一解决的思想方法,叫做消元思想.
把二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解. 这种方法叫做代入消元法,简称代入法.
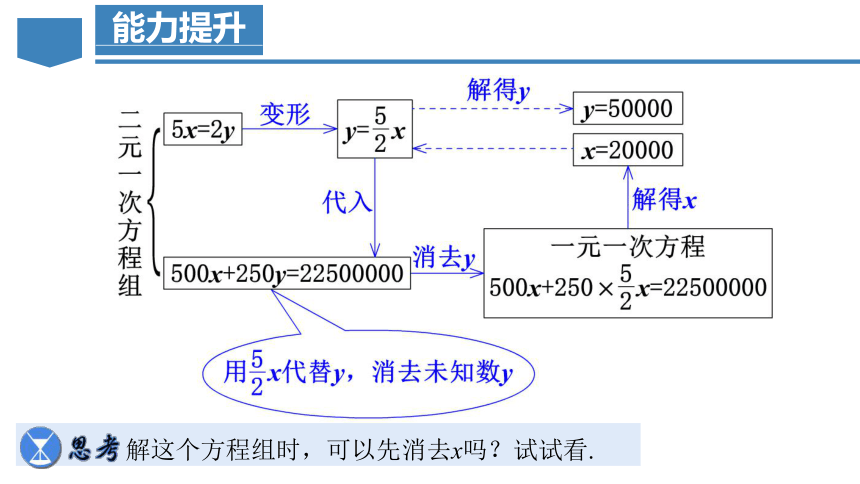
解这个方程组时,可以先消去x吗?试试看.
用含一个未知数的式子表示另一个未知数
基础
例1.把下列方程改写成用含x的式子表示y的形式:
(1)2x-y=5; (2)x+y=4.
解:(1)移项,得-y=5-2x.
系数化为1,得y=2x-5.
(2)移项,得二y=4-x.
系数化为1,得y=8-x.
【1-1】将方程2x+y=3写成用含x的式子表示y的形式,正确的是( )
A.y=2x-3 B.y=3-2x C.x= D.x=
【1-2】已知3x-2y-5=0,用含x的式子表示y:_______________.
【1-3】将4y+8=2x+3写成用y表示x的形式为_____________.
B
y=x
x=y
用代入消元法解二元一次方 程组
重点
例2.用代入法解下列方程组:
(1) (2)
解:(1)把①代入②,得 2x-3(3x+1)=4.
解这个方程,得 x=-1.
把x=-1代入①,得 y=-2.
所以这个方程组的解是
注意:代入时此处一定要带括号
用代入消元法解二元一次方 程组
重点
例2.用代入法解下列方程组:
(1) (2)
(2)由①,得y=3x-7.③
把③代入②,得2x+3(3x-7)=-5.
解这个方程,得x= .
把x= 代入③,得y=.
所以这个方程组的解是
注意:代入时此处一定要带括号
【2-1】对于二元一次方程组将①式代入②式,消去y可以得到( )
A. x+2x-1=7 B. x+2x-2=7 C. x+x-1=7 D. x+2x+2=7
【2-2】用代入消元法解二元一次方程组使得代入后化简比
较容易的变形是( )
A.由①得x= B.由①得y= C.由②得x= D.由②得y=2x-5
B
D
【2-3】用代入法解下列方程组:
(1) (2)
解:(1)由①,得x=1+2y.③
把③代入②,得2(1+2y)+y=-3.
解这个方程,得y=-1.
把y=-1代入③,得x=-1.
所以这个方程组的解是
(2)由①,得x=3-y.③
把③代入②,得3-y-1=.
解这个方程,得y=2.
把y=2代入③,得x=1.
所以这个方程组的解是
【2-3】用代入法解下列方程组:
(1) (2)
(3)由①,得n=4m.③
把③代入②,得5m-6(4m)=33.
解这个方程,得m=6.
把m=6代入③,得n=-.
所以这个方程组的解是
用代入消元法解二元一次方程组解决实际问题
重点
例3. 某天,蔬菜经营户老李用145元从蔬菜批发市场批发了一些黄瓜和茄子到菜市场售卖,黄瓜和茄子当天的批发价与零售价如下表所示.当天他卖完这些黄瓜和茄子共赚了90元.这天老李批发的黄瓜和茄子分别有多少千克
用代入消元法解二元一次方程组解决实际问题
重点
例3. 某天,蔬菜经营户老李用145元从蔬菜批发市场批发了一些黄瓜和茄子到菜市场售卖,黄瓜和茄子当天的批发价与零售价如下表所示.当天他卖完这些黄瓜和茄子共赚了90元.这天老李批发的黄瓜和茄子分别有多少千克
解:设这天老李批发的黄瓜有x kg,茄子有y kg.
由题意,得解得
解得
答:这天老李批发的黄瓜有15 kg,茄子有25 kg.
【3-1】某铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km,则隧道累计长度为_______km.
【3-2】某停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为8元/辆.现在停车场内停有30辆中、小型汽车,这些车共缴纳停车费324元.中、小型汽车各有多少辆
126
解:设中型汽车有x辆,小型汽车有y辆.
由题意,得解得
答:中型汽车有12辆,小型汽车有18辆.
利用二元一次方程组的解的关系求字母的值
重点
例4.已知关于x,y的方程组的解满足方程x+y=8,求m的值.
解:把②代入①,得3x+5y=2x+3y+2.
化简,得x+2y= 2.③
把③与x+y=8联立组成方程组,得
解这个方程组,得
利用二元一次方程组的解的关系求字母的值
重点
例4.已知关于x,y的方程组的解满足方程x+y=8,求m的值.
把代入②,得2×14+3×(-6)=m.
所以m=10.
【4-1】已知方程组的解x,y满足x比y的2倍少3,则a的值为( )
A.-41 B.-11 C.-31 D.-22
【4-2】已知关于x,y的方程组的解也是方程x+y=3的解,求m的值.
C
解:将2x+y=1与x+y=3组成方程组
解这个方程组,得
将代入x+2y=m,得m=8.
【4-3】已知关于x,y的方程组的解满足x+y=0,求a的值.
解:因为x+y=0,所以x=-y.③
把③代入①,得2y=-1-3a;
把③代入②,得2y= 1-a.
所以-1-3a=1-a.
解这个方程,得a=-1.
构造二元一次方程组的模型求字母的值
重点
例5.【转化思想】已知|a+2b+3|+=0,求(3a+2b)2025的值.
解:因为|a+2b+3|+ =0,
所以
由②,得b=3a-5.③
把③代入①,得a+2(3a-5)+3=0.
解这个方程,得a=1.
把a=1代入③,得b=-2.
所以(3a+2b)2025=[3×1+2×(-2)]2025=-1.
【5-1】已知关于x,y的方程x2m-n-2+4ym+n+l=6是二元一次方程,则m,n的值分别为( )
A.m=1,n=-1 B.m=-1,n=1 C.m=,n= D.m=,n=
【5-2】已知式子-3xm-1y3与xnym+n是同类项,则m=_____,n=_____.
【5-3】在平面直角坐标系中,已知点A(m+2n,4m-3n)位于第一象限,点A 到x轴的距离为1,到y轴的距离为3,则2m-n的值为_______.
A
2
1
1
用“整体代入法”解方程组
难点
例6.先阅读材料,然后解方程组.
材料:解方程组:
解:由①,得x-y=1.③
把③代入②,得4x1-y=5.
解这个方程,得y=-1.
把y=-1代入③,得x=0.
所以这个方程组的解是
这种方法被称为“整体代入法”.
请用这种方法解方程组:
解:由①,得2x-3y=2.③
把③代入②,得+2y=9.
解这个方程,得y=4.
把y=4代入③,得x=7.
所以这个方程组的解是
【6-1】解方程组的最佳方法是( )
A.由①得m=再代入② B.由②得m=再代入①
C.由①得3m=7+4n再代入② D.由②得9m=10n- -25再代入①
C
【6-2】用代入法解下列方程组:
(1) (2)
解:由②,得x-3=4y.③
把③代入①,得2×4y+3y=11.
解这个方程,得y=1.
把y=1代入③,得x=7.
所以这个方程组的解是
解:由②,得x+1=3-2(y-1).③
把③代入①,得6-4(y-1)+3(y-1)=5.
解这个方程,得y=2.
把y=2代入③,得x=0.
所以这个方程组的解是
第8章 二元一次方程组
8.2.1 二元一次方程组的解法
(代入消元法)
第四单元
1.掌握代入消元法的意义;
2.会用代入法解二元一次方程组. (重点、难点)
1.把下列方程写成用含x的式子表示y的形式.
(1) 2x+y=6
(2) y-3x-1=0
2.你能把上面两个方程写成用含y的式子表示x的形式.
3.如何解这样的方程组 .
y=6-2x
y=3x+1
(1)
(2)
一个苹果和一个梨的质量合计200g;
这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等.
问题1:观察下面两个天平你能从中得到哪些信息?
问题2:问苹果和梨的质量各是多少g?你会列出方程组吗?
x克
y克
x克
y克
x+(x+10)=200
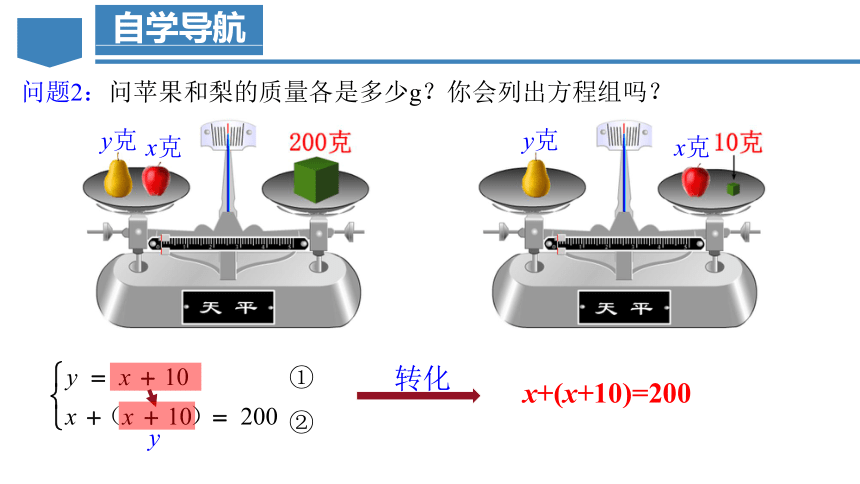
问题2:问苹果和梨的质量各是多少g?你会列出方程组吗?
x克
y克
x克
y克
x+(x+10)=200
①②
y
转化
x+(x+10)=200
①②
y
转化
x=95
y=105
所以原方程组的解是
求方程组解的过程叫做解方程组.
将未知数的个数由多化少、逐一解决的思想方法,叫做消元思想.
把二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解. 这种方法叫做代入消元法,简称代入法.
解这个方程组时,可以先消去x吗?试试看.
用含一个未知数的式子表示另一个未知数
基础
例1.把下列方程改写成用含x的式子表示y的形式:
(1)2x-y=5; (2)x+y=4.
解:(1)移项,得-y=5-2x.
系数化为1,得y=2x-5.
(2)移项,得二y=4-x.
系数化为1,得y=8-x.
【1-1】将方程2x+y=3写成用含x的式子表示y的形式,正确的是( )
A.y=2x-3 B.y=3-2x C.x= D.x=
【1-2】已知3x-2y-5=0,用含x的式子表示y:_______________.
【1-3】将4y+8=2x+3写成用y表示x的形式为_____________.
B
y=x
x=y
用代入消元法解二元一次方 程组
重点
例2.用代入法解下列方程组:
(1) (2)
解:(1)把①代入②,得 2x-3(3x+1)=4.
解这个方程,得 x=-1.
把x=-1代入①,得 y=-2.
所以这个方程组的解是
注意:代入时此处一定要带括号
用代入消元法解二元一次方 程组
重点
例2.用代入法解下列方程组:
(1) (2)
(2)由①,得y=3x-7.③
把③代入②,得2x+3(3x-7)=-5.
解这个方程,得x= .
把x= 代入③,得y=.
所以这个方程组的解是
注意:代入时此处一定要带括号
【2-1】对于二元一次方程组将①式代入②式,消去y可以得到( )
A. x+2x-1=7 B. x+2x-2=7 C. x+x-1=7 D. x+2x+2=7
【2-2】用代入消元法解二元一次方程组使得代入后化简比
较容易的变形是( )
A.由①得x= B.由①得y= C.由②得x= D.由②得y=2x-5
B
D
【2-3】用代入法解下列方程组:
(1) (2)
解:(1)由①,得x=1+2y.③
把③代入②,得2(1+2y)+y=-3.
解这个方程,得y=-1.
把y=-1代入③,得x=-1.
所以这个方程组的解是
(2)由①,得x=3-y.③
把③代入②,得3-y-1=.
解这个方程,得y=2.
把y=2代入③,得x=1.
所以这个方程组的解是
【2-3】用代入法解下列方程组:
(1) (2)
(3)由①,得n=4m.③
把③代入②,得5m-6(4m)=33.
解这个方程,得m=6.
把m=6代入③,得n=-.
所以这个方程组的解是
用代入消元法解二元一次方程组解决实际问题
重点
例3. 某天,蔬菜经营户老李用145元从蔬菜批发市场批发了一些黄瓜和茄子到菜市场售卖,黄瓜和茄子当天的批发价与零售价如下表所示.当天他卖完这些黄瓜和茄子共赚了90元.这天老李批发的黄瓜和茄子分别有多少千克
用代入消元法解二元一次方程组解决实际问题
重点
例3. 某天,蔬菜经营户老李用145元从蔬菜批发市场批发了一些黄瓜和茄子到菜市场售卖,黄瓜和茄子当天的批发价与零售价如下表所示.当天他卖完这些黄瓜和茄子共赚了90元.这天老李批发的黄瓜和茄子分别有多少千克
解:设这天老李批发的黄瓜有x kg,茄子有y kg.
由题意,得解得
解得
答:这天老李批发的黄瓜有15 kg,茄子有25 kg.
【3-1】某铁路途经许多隧道和桥梁,其中隧道累计长度与桥梁累计长度之和为342km,隧道累计长度的2倍比桥梁累计长度多36km,则隧道累计长度为_______km.
【3-2】某停车场的收费标准如下:中型汽车的停车费为15元/辆,小型汽车的停车费为8元/辆.现在停车场内停有30辆中、小型汽车,这些车共缴纳停车费324元.中、小型汽车各有多少辆
126
解:设中型汽车有x辆,小型汽车有y辆.
由题意,得解得
答:中型汽车有12辆,小型汽车有18辆.
利用二元一次方程组的解的关系求字母的值
重点
例4.已知关于x,y的方程组的解满足方程x+y=8,求m的值.
解:把②代入①,得3x+5y=2x+3y+2.
化简,得x+2y= 2.③
把③与x+y=8联立组成方程组,得
解这个方程组,得
利用二元一次方程组的解的关系求字母的值
重点
例4.已知关于x,y的方程组的解满足方程x+y=8,求m的值.
把代入②,得2×14+3×(-6)=m.
所以m=10.
【4-1】已知方程组的解x,y满足x比y的2倍少3,则a的值为( )
A.-41 B.-11 C.-31 D.-22
【4-2】已知关于x,y的方程组的解也是方程x+y=3的解,求m的值.
C
解:将2x+y=1与x+y=3组成方程组
解这个方程组,得
将代入x+2y=m,得m=8.
【4-3】已知关于x,y的方程组的解满足x+y=0,求a的值.
解:因为x+y=0,所以x=-y.③
把③代入①,得2y=-1-3a;
把③代入②,得2y= 1-a.
所以-1-3a=1-a.
解这个方程,得a=-1.
构造二元一次方程组的模型求字母的值
重点
例5.【转化思想】已知|a+2b+3|+=0,求(3a+2b)2025的值.
解:因为|a+2b+3|+ =0,
所以
由②,得b=3a-5.③
把③代入①,得a+2(3a-5)+3=0.
解这个方程,得a=1.
把a=1代入③,得b=-2.
所以(3a+2b)2025=[3×1+2×(-2)]2025=-1.
【5-1】已知关于x,y的方程x2m-n-2+4ym+n+l=6是二元一次方程,则m,n的值分别为( )
A.m=1,n=-1 B.m=-1,n=1 C.m=,n= D.m=,n=
【5-2】已知式子-3xm-1y3与xnym+n是同类项,则m=_____,n=_____.
【5-3】在平面直角坐标系中,已知点A(m+2n,4m-3n)位于第一象限,点A 到x轴的距离为1,到y轴的距离为3,则2m-n的值为_______.
A
2
1
1
用“整体代入法”解方程组
难点
例6.先阅读材料,然后解方程组.
材料:解方程组:
解:由①,得x-y=1.③
把③代入②,得4x1-y=5.
解这个方程,得y=-1.
把y=-1代入③,得x=0.
所以这个方程组的解是
这种方法被称为“整体代入法”.
请用这种方法解方程组:
解:由①,得2x-3y=2.③
把③代入②,得+2y=9.
解这个方程,得y=4.
把y=4代入③,得x=7.
所以这个方程组的解是
【6-1】解方程组的最佳方法是( )
A.由①得m=再代入② B.由②得m=再代入①
C.由①得3m=7+4n再代入② D.由②得9m=10n- -25再代入①
C
【6-2】用代入法解下列方程组:
(1) (2)
解:由②,得x-3=4y.③
把③代入①,得2×4y+3y=11.
解这个方程,得y=1.
把y=1代入③,得x=7.
所以这个方程组的解是
解:由②,得x+1=3-2(y-1).③
把③代入①,得6-4(y-1)+3(y-1)=5.
解这个方程,得y=2.
把y=2代入③,得x=0.
所以这个方程组的解是
