多边形的内角和与外角和
图片预览










文档简介
课件31张PPT。多边形的内角和与外角和问题:1.什么叫做三角形? 三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形。2.三角形的内角和定理是什么?外角和定理呢?三角形的内角和是三角形的外角和是多边形的内角和
与外角和 (1) 三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形。(2)四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形。记作记作(3)五边形是由五条不在同一直线上的线段首尾顺次连结组成的平面图形。记作 一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形。凹多边形凸多边形顶点内角边外角对角线对角线:在多边形中,连接不相邻的两个顶
点的线段叫做多边形的对角线。外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。问题 1 五边形、六边形分别有多少个内角?多少个外角?答 五边形有5个内角,10个(5对)外角;
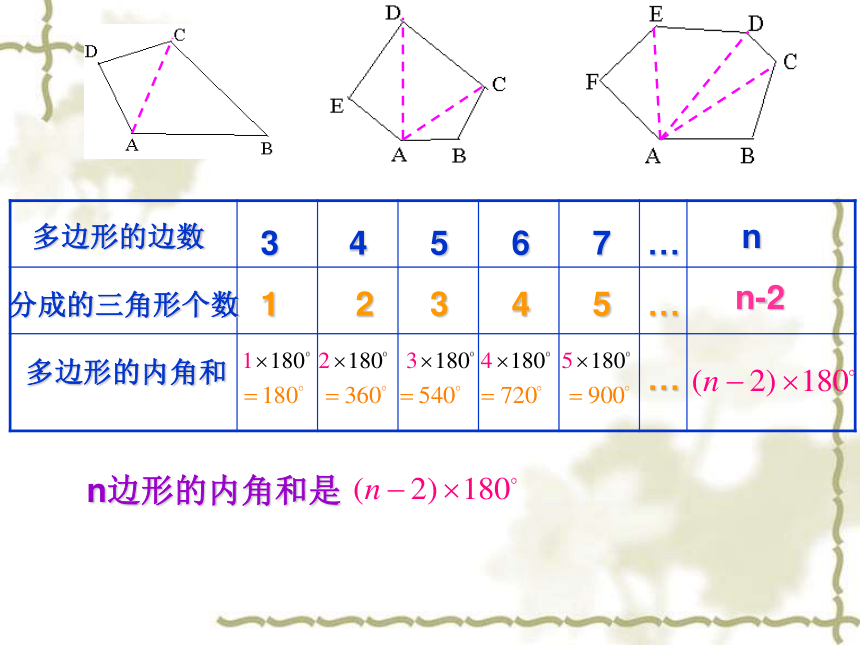
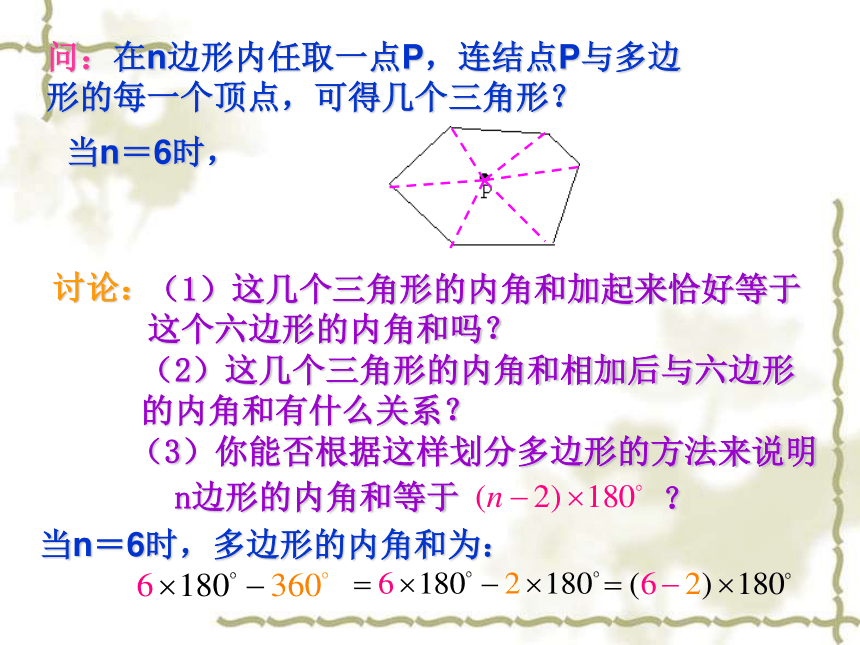
六边形有6个内角,12个(6对)外角.问题 n边形有多少个内角?多少个外角?答 n边形有n个内角,2n个(n对)外角. 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.如:正三角形、正四边形(正方形)、正五边形等.多边形的边数分成的三角形个数多边形的内角和3456…n1234…n-275…n边形的内角和是 问:在n边形内任取一点P,连结点P与多边形的每一个顶点,可得几个三角形?当n=6时,(3)你能否根据这样划分多边形的方法来说明?n边形的内角和等于当n=6时,多边形的内角和为:讨论:(1)这几个三角形的内角和加起来恰好等于这个六边形的内角和吗?(2)这几个三角形的内角和相加后与六边形的内角和有什么关系?练习:在n边形某边上任取一点P,连结点P与多边形的每一个顶点,可得多少个三角形?你能否根据这样划分多?(图中取n=5的情形)边形的方法来说明n边形的内角和等于(3)你能否根据这样划分多边形的方法来说明?n边形的内角和等于讨论:(1)这几个三角形的内角和加起来恰好等于这个五边形的内角和吗?(2)这几个三角形的内角和相加后与五边形的内角和有什么关系?问:以上三种求多边形内角和的方法有什么共同之处?把多边形划分成若干个三角形,再利用三角形的求出多边形的内角和 内角和为例1、求八边形的内角和的度数。解:八边形的内角和度数为:练习:已知一个多边形的内角和是则这个多边形是 边形 .十五15从与三角形的每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。问:多边形的每一个内角和与它相邻的外角有什么关系?多边形的边数多边形的内角与外角的总和多边形的内角和多边形的外角和3456…n7………任意多边形的外角和都为:多边形的外角和与边数无关。正n边形的每个内角的度数为:正n边形的每个外角的度数为:练习:(1)十边形的内角和是,外角和是;如果十边形的各个内角都相等,那么它的一个内角是.(2)在一个多边形中,它的内角最多可以有几个是锐角?3个小结:1. n边形的内角和定理是什么?2.推导多边形内角和定理时所用的方法是什么?3.多边形的外角和定理是什么?4.多边形的内角与其相邻外角的和是多少?5.多边形的内角与外角在计算中的相互转化。把多边形划分成若干个三角形,再利用三角形的求出多边形的内角和 内角和为任意多边形的外角和都为:n边形的内角和为试一试 请大家思考:五边形ABCDE共有几条对角线呢?五边形ABCDE共有5条对角线。请大家思考:六边形ABCDEF共有几条对角线呢?试一试 六边形ABCDEF共有9条对角线。有没有什么
规律呢?请问:四边形从一个顶点出发,能引出几条对角线?请问:五边形从一个顶点出发,能引出几条对角线?请问:六边形从一个顶点出发,能引出几条对角线?请问:N边形从一个顶点出发,能引出几条对角线? ……123N-3探索新知 请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?34567n180 °36 0 °540 °720 °900 °180 ° n-360°3.从多边形内一个点出发[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是 例题赏析(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. [例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是 例题赏析(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. 例2 一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
分析 正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.设一个外角为x°,则内角为(x+36)°因为多边形的内角与相邻的外角互补;所以 x+x+36=180解得 x=72360÷72=5答 这个多边形的五边形.解例3 (1)四边形有几条对角线?
(2)五边形有几条对角线?六边形呢?n边形呢?(1)四边形有两条对角线,(2)如图,以A为端点的对角线有两条AC、AD同样以B为端点的对角线也有2条,以C为端点也有2条,但AC与CA是同一条线段,以D为端点的两条DA、DB与AD、BD分别表示同一条线段,所以只有5条,以此类推六边形有9条对角线,从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条,那么n个顶点就有n(n-3)条,但其中每一条都重复计算一次,所以n边形一共有 条对角线.解:思考:1、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:2、求∠A+ ∠B+ ∠C+ ∠D
+ ∠E+ ∠F + ∠G+ ∠H的值思考:ABEDFC3、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:4、求∠A+ ∠B+ ∠C+ ∠D
+ ∠E+ ∠F + ∠G的值1条2条3条多边形的边数一个顶点引出的对角线条数多边形的对角线总条数4567…n1234…n-385n边形中,由一个顶点引出的对角线条数为:n-3n边形的对角线总条数为:
与外角和 (1) 三角形是由三条不在同一直线上的线段首尾顺次连结组成的平面图形。(2)四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形。记作记作(3)五边形是由五条不在同一直线上的线段首尾顺次连结组成的平面图形。记作 一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形。凹多边形凸多边形顶点内角边外角对角线对角线:在多边形中,连接不相邻的两个顶
点的线段叫做多边形的对角线。外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。问题 1 五边形、六边形分别有多少个内角?多少个外角?答 五边形有5个内角,10个(5对)外角;
六边形有6个内角,12个(6对)外角.问题 n边形有多少个内角?多少个外角?答 n边形有n个内角,2n个(n对)外角. 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.如:正三角形、正四边形(正方形)、正五边形等.多边形的边数分成的三角形个数多边形的内角和3456…n1234…n-275…n边形的内角和是 问:在n边形内任取一点P,连结点P与多边形的每一个顶点,可得几个三角形?当n=6时,(3)你能否根据这样划分多边形的方法来说明?n边形的内角和等于当n=6时,多边形的内角和为:讨论:(1)这几个三角形的内角和加起来恰好等于这个六边形的内角和吗?(2)这几个三角形的内角和相加后与六边形的内角和有什么关系?练习:在n边形某边上任取一点P,连结点P与多边形的每一个顶点,可得多少个三角形?你能否根据这样划分多?(图中取n=5的情形)边形的方法来说明n边形的内角和等于(3)你能否根据这样划分多边形的方法来说明?n边形的内角和等于讨论:(1)这几个三角形的内角和加起来恰好等于这个五边形的内角和吗?(2)这几个三角形的内角和相加后与五边形的内角和有什么关系?问:以上三种求多边形内角和的方法有什么共同之处?把多边形划分成若干个三角形,再利用三角形的求出多边形的内角和 内角和为例1、求八边形的内角和的度数。解:八边形的内角和度数为:练习:已知一个多边形的内角和是则这个多边形是 边形 .十五15从与三角形的每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。问:多边形的每一个内角和与它相邻的外角有什么关系?多边形的边数多边形的内角与外角的总和多边形的内角和多边形的外角和3456…n7………任意多边形的外角和都为:多边形的外角和与边数无关。正n边形的每个内角的度数为:正n边形的每个外角的度数为:练习:(1)十边形的内角和是,外角和是;如果十边形的各个内角都相等,那么它的一个内角是.(2)在一个多边形中,它的内角最多可以有几个是锐角?3个小结:1. n边形的内角和定理是什么?2.推导多边形内角和定理时所用的方法是什么?3.多边形的外角和定理是什么?4.多边形的内角与其相邻外角的和是多少?5.多边形的内角与外角在计算中的相互转化。把多边形划分成若干个三角形,再利用三角形的求出多边形的内角和 内角和为任意多边形的外角和都为:n边形的内角和为试一试 请大家思考:五边形ABCDE共有几条对角线呢?五边形ABCDE共有5条对角线。请大家思考:六边形ABCDEF共有几条对角线呢?试一试 六边形ABCDEF共有9条对角线。有没有什么
规律呢?请问:四边形从一个顶点出发,能引出几条对角线?请问:五边形从一个顶点出发,能引出几条对角线?请问:六边形从一个顶点出发,能引出几条对角线?请问:N边形从一个顶点出发,能引出几条对角线? ……123N-3探索新知 请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?34567n180 °36 0 °540 °720 °900 °180 ° n-360°3.从多边形内一个点出发[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是 例题赏析(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. [例1]一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是 例题赏析(n-2)·180°,外角和等于360°,所以:(n-2)·180=3×360解得:n=8答:这个多边形是八边形. 例2 一个正多边形的一个内角比相邻外角大36°,求这个正多边形的边数.
分析 正多边形的各个内角都相等,那么各个外角也都相等,而多边形的外角和是360°.设一个外角为x°,则内角为(x+36)°因为多边形的内角与相邻的外角互补;所以 x+x+36=180解得 x=72360÷72=5答 这个多边形的五边形.解例3 (1)四边形有几条对角线?
(2)五边形有几条对角线?六边形呢?n边形呢?(1)四边形有两条对角线,(2)如图,以A为端点的对角线有两条AC、AD同样以B为端点的对角线也有2条,以C为端点也有2条,但AC与CA是同一条线段,以D为端点的两条DA、DB与AD、BD分别表示同一条线段,所以只有5条,以此类推六边形有9条对角线,从以上分析可知从n边形的一个顶点引对角线,可以引(n-3)条,那么n个顶点就有n(n-3)条,但其中每一条都重复计算一次,所以n边形一共有 条对角线.解:思考:1、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:2、求∠A+ ∠B+ ∠C+ ∠D
+ ∠E+ ∠F + ∠G+ ∠H的值思考:ABEDFC3、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:4、求∠A+ ∠B+ ∠C+ ∠D
+ ∠E+ ∠F + ∠G的值1条2条3条多边形的边数一个顶点引出的对角线条数多边形的对角线总条数4567…n1234…n-385n边形中,由一个顶点引出的对角线条数为:n-3n边形的对角线总条数为:
