8.3.3 实际问题与二元一次方程组(第三课时) 课件(共30张PPT)
文档属性
| 名称 | 8.3.3 实际问题与二元一次方程组(第三课时) 课件(共30张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 13:33:25 | ||
图片预览






文档简介
(共30张PPT)
第8章 二元一次方程组
8.3.3 实际问题与二元一次方程组(3)
第四单元
1.能够根据具体的数量关系,列出二元一次方程组解决复杂的实际问题;
(重点)
2.学会利用二元一次方程组解决图表信息、决策、商品等问题.(重点、难点)
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
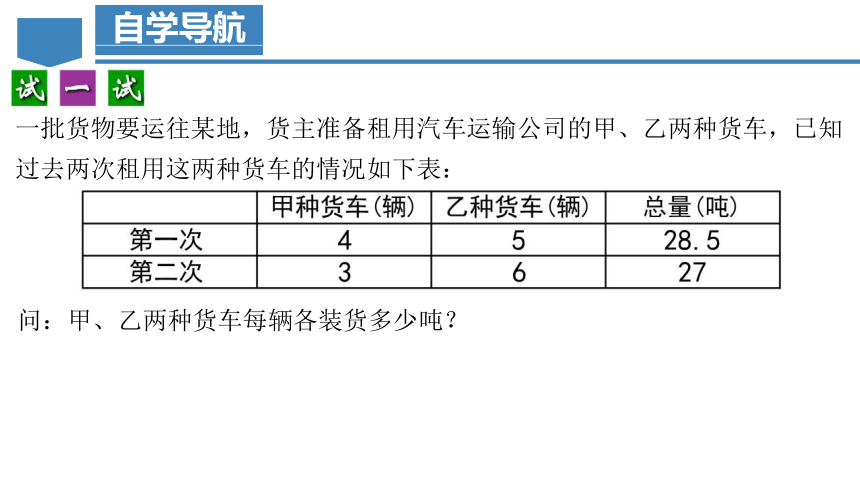
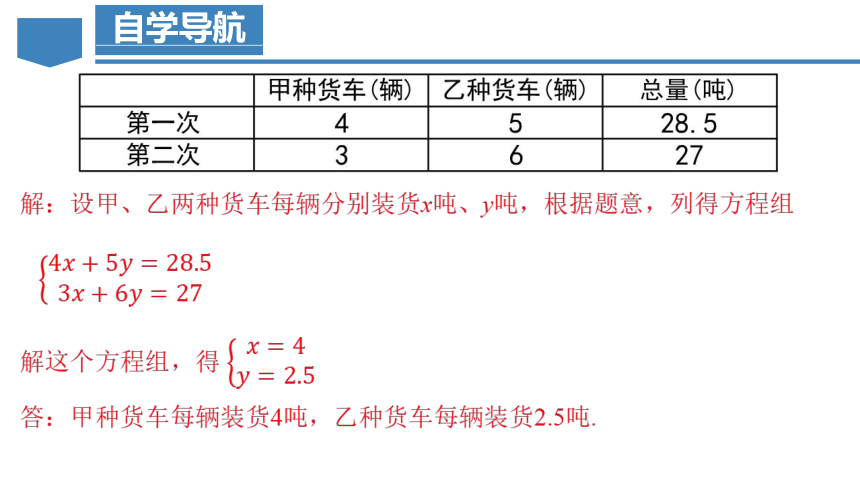
一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
问:甲、乙两种货车每辆各装货多少吨?
解:设甲、乙两种货车每辆分别装货x吨、y吨,根据题意,列得方程组
解这个方程组,得
答:甲种货车每辆装货4吨,乙种货车每辆装货2.5吨.
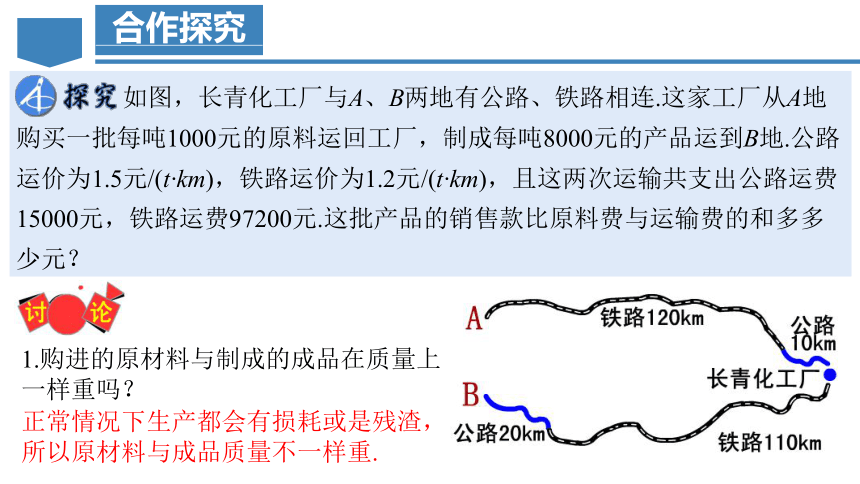
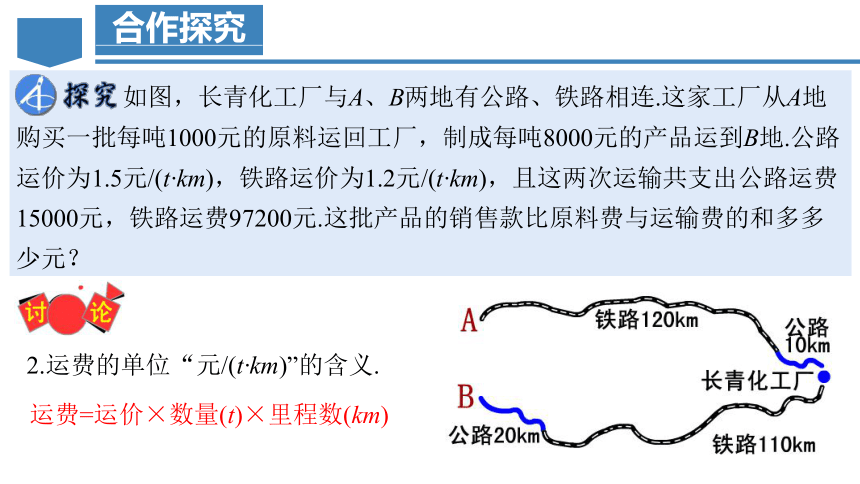
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
1.购进的原材料与制成的成品在质量上一样重吗?
正常情况下生产都会有损耗或是残渣,所以原材料与成品质量不一样重.
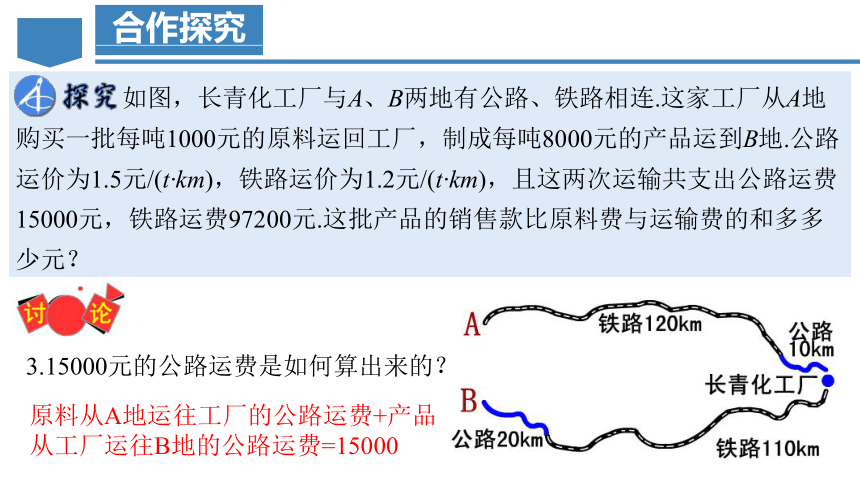
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
2.运费的单位“元/(t·km)”的含义.
运费=运价×数量(t)×里程数(km)
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
3.15000元的公路运费是如何算出来的?
原料从A地运往工厂的公路运费+产品从工厂运往B地的公路运费=15000
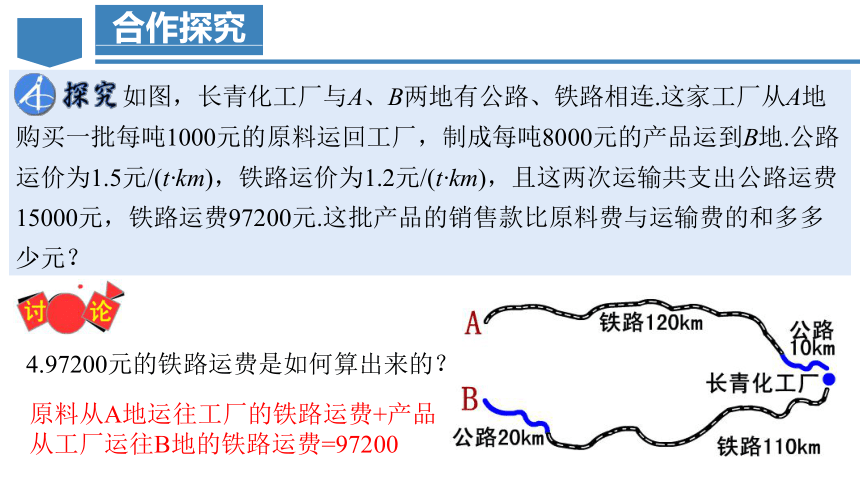
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
4.97200元的铁路运费是如何算出来的?
原料从A地运往工厂的铁路运费+产品从工厂运往B地的铁路运费=97200
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
分
析
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关. 因此设_____________________________.
制成 x t产品, 购买 y t原料
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
解:设制成x t产品,购买y t原料.由上表,列得方程组
解这个方程组,得
销售款-(原料费+运输费)=8000x-(1000y+15000+97200)=1887800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
图表信息问题
重点
例1.请你根据图中的对话信息,求中性笔和笔记本的单价.
解:设中性笔和笔记本的单价分别是x元、y元.
根据题意,得
解得
答:中性笔的单价是2元,笔记本的单价是6元.
1.某中学七年级( 1)班40名同学为灾区共捐款2000元,捐款情况如表所示:
表格中捐款40元和50元的人数不小心被污渍污染已看不清楚,若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可列方程组为( )
A. B.
C. D.
C
2.小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元.
解:设中性笔和笔记本的单价分别是x元、
y元.
根据题意可得
解得
答:中性笔和笔记本的单价分别是2元、6元.
3.某景点的门票价格如下表:
某校八、九年级学生自愿报名游览该景点,其中八年级的报名人数不超过50,九年级的报名人数超过50但不超过80.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元.
八、九年级的报名人数各是多少
解:因为4452÷45=98
98不是整数,
所以两个年级人数之和超过99.
设八年级的报名人数是x,九年级的报名人数是y.
依题意,得
解得
答:八年级的报名人数是48,九年级的报名人数是58.
例2.某服装店用6000元购进A,B两种服装,按标价全部售出后可获得利润3800元,这两种服装的进价、标价如表所示.
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的八折出售,B种服装按标价的七折出售,那么这批服装全部售完后,相比按标价出售,利润减少多少元
经济生活问题
重点
经济生活问题
重点
解:(1)设A种服装购进x件,B种服装购进y件.
由题意,得
解得
答:A种服装购进50件,B种服装购进30件.
(2)由题意,得
3800-50(100×0.8-60) -30(160×0.7-100)=3800- I 000- 360=2440(元).
答:相比按标价出售,利润减少2440元.
1.某商场为迎接店庆进行促销,羊绒衫每件按标价的八折出售,每件赚70元,后因库存太多,每件羊绒衫按标价的六折出售,每件亏损110元,则该商场每件羊绒衫的进价为______元,标价为______元.
2.某工厂现向银行申请了两种贷款,共计35万元,每年需付利息2.25万元,甲种贷款每年的利率是7%,乙种贷款每年的利率是6%.若设甲、乙两种贷款的数额分别为x万元和y万元,则x=_____,y=_____.
650
900
15
20
3.某商场按标价销售某种商品时,每件可获利40元;按标价的八折销售该商品5件与将标价降低30元销售该商品3件所获得的利润相等.求该商品每件的进价和标价.
解:设该商品每件的进价为x元,标价为y元.
根据题意,得
解得
答:该商品每件的进价和标价分别是130 元、170元.
4.在某体育用品商店购买50根跳绳和80个毽子共需1120元,购买30根跳绳和50个毽子共需680元.
(1)跳绳、 毽子的单价各是多少元
(2)在“元旦”期间,该店开展促销活动,所有商品按同样的折扣打折销售,若购买100 根跳绳和100个毽子只需1700元,则该店的商品按原价的几折进行销售
解:(1)设跳绳的单价为x元,毽子的单价为y元.
依题意,得
解得
答:跳绳的单价为16元,毽子的单价为4元.
(2)设该店的商品按原价的m折进行销售.
依题意,得16×100+4××100=1700,
解得 m=8.5.
答:该店的商品按原价的八五折进行销售.
利用二元一次方程组进行决策
重点
例3.某生态柑橘园现有柑橘21吨,计划租用A、B两种型号的货车将柑橘运往外地销售.已知满载时,用3辆A型车和2辆B型车一次可运柑橘13吨;用4辆A型车和3辆B型车一次可运柑橘18吨.
(1)1辆A型车和1辆B型车满载时,一次分别运柑橘多少吨
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案.
利用二元一次方程组进行决策
重点
(1)1辆A型车和1辆B型车满载时,一次分别运柑橘多少吨
解:设满载时1辆A型车一次可运柑橘x吨,1辆B型车一次可运柑橘y吨.
依题意,得
解得
答:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
利用二元一次方程组进行决策
重点
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案.
解:依题意,得3m+2n=21,∴m=7-n.
又∵m,n均为非负整数,
∴或或或
答:共有4种租车方案.
方案1:租用1辆A型车,9辆B型车;
方案2:租用3辆A型车,6辆B型车;
方案3:租用5辆A型车,3辆B型车;
方案4:只租用7辆A型车.
1.某中学组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少 原计划租用45座客车多少辆
解:设这批学生的人数是x,原计划租用45座客车y辆.
根据题意,得
解得
答:这批学生的人数为240,原计划租用45座客车5辆.
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算
解:租45座客车:240÷45≈5.3(辆),
所以需租6辆,租金为220×6=1320(元);
租60座客车: 240÷60=4(辆),
所以需租4辆,租金为300×4=1200(元).
因为1200<1320,所以租用4辆60座客车才合算.
答:租用4辆60座客车才合算.
2.妈妈去超市买牙刷和牙膏,已知购买4支牙刷和2盒牙膏需付68元;购买10支牙刷和7盒牙膏需付210元.
(1)求牙刷和牙膏的单价;
解:设牙刷的单价为x元,牙膏的单价为y元.
依题意得
解得
答:牙刷的单价为7元,牙膏的单价为20元.
(2)正好赶上甲、乙两个超市打折优惠,两个超市的每个物品的原价均相同.甲超市:牙刷打九折,牙膏打八折;乙超市:每购买满10盒牙膏送3支牙刷.如果妈妈打算买13 盒牙膏和18支牙刷,那么去哪家超市比较划算 并说明理由.
解:去甲超市比较划算.理由如下:
在甲超市购买所需费用为18×7×0.9+13×20×0.8=321.4(元);
在乙超市购买所需费用为13×20+(18-3)×7=365(元).
∵365>321.4,
∴去甲超市比较划算.
第8章 二元一次方程组
8.3.3 实际问题与二元一次方程组(3)
第四单元
1.能够根据具体的数量关系,列出二元一次方程组解决复杂的实际问题;
(重点)
2.学会利用二元一次方程组解决图表信息、决策、商品等问题.(重点、难点)
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用__________法或___________解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
问:甲、乙两种货车每辆各装货多少吨?
解:设甲、乙两种货车每辆分别装货x吨、y吨,根据题意,列得方程组
解这个方程组,得
答:甲种货车每辆装货4吨,乙种货车每辆装货2.5吨.
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
1.购进的原材料与制成的成品在质量上一样重吗?
正常情况下生产都会有损耗或是残渣,所以原材料与成品质量不一样重.
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
2.运费的单位“元/(t·km)”的含义.
运费=运价×数量(t)×里程数(km)
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
3.15000元的公路运费是如何算出来的?
原料从A地运往工厂的公路运费+产品从工厂运往B地的公路运费=15000
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
4.97200元的铁路运费是如何算出来的?
原料从A地运往工厂的铁路运费+产品从工厂运往B地的铁路运费=97200
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
分
析
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关. 因此设_____________________________.
制成 x t产品, 购买 y t原料
如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
解:设制成x t产品,购买y t原料.由上表,列得方程组
解这个方程组,得
销售款-(原料费+运输费)=8000x-(1000y+15000+97200)=1887800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
图表信息问题
重点
例1.请你根据图中的对话信息,求中性笔和笔记本的单价.
解:设中性笔和笔记本的单价分别是x元、y元.
根据题意,得
解得
答:中性笔的单价是2元,笔记本的单价是6元.
1.某中学七年级( 1)班40名同学为灾区共捐款2000元,捐款情况如表所示:
表格中捐款40元和50元的人数不小心被污渍污染已看不清楚,若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可列方程组为( )
A. B.
C. D.
C
2.小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元.
解:设中性笔和笔记本的单价分别是x元、
y元.
根据题意可得
解得
答:中性笔和笔记本的单价分别是2元、6元.
3.某景点的门票价格如下表:
某校八、九年级学生自愿报名游览该景点,其中八年级的报名人数不超过50,九年级的报名人数超过50但不超过80.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元.
八、九年级的报名人数各是多少
解:因为4452÷45=98
98不是整数,
所以两个年级人数之和超过99.
设八年级的报名人数是x,九年级的报名人数是y.
依题意,得
解得
答:八年级的报名人数是48,九年级的报名人数是58.
例2.某服装店用6000元购进A,B两种服装,按标价全部售出后可获得利润3800元,这两种服装的进价、标价如表所示.
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的八折出售,B种服装按标价的七折出售,那么这批服装全部售完后,相比按标价出售,利润减少多少元
经济生活问题
重点
经济生活问题
重点
解:(1)设A种服装购进x件,B种服装购进y件.
由题意,得
解得
答:A种服装购进50件,B种服装购进30件.
(2)由题意,得
3800-50(100×0.8-60) -30(160×0.7-100)=3800- I 000- 360=2440(元).
答:相比按标价出售,利润减少2440元.
1.某商场为迎接店庆进行促销,羊绒衫每件按标价的八折出售,每件赚70元,后因库存太多,每件羊绒衫按标价的六折出售,每件亏损110元,则该商场每件羊绒衫的进价为______元,标价为______元.
2.某工厂现向银行申请了两种贷款,共计35万元,每年需付利息2.25万元,甲种贷款每年的利率是7%,乙种贷款每年的利率是6%.若设甲、乙两种贷款的数额分别为x万元和y万元,则x=_____,y=_____.
650
900
15
20
3.某商场按标价销售某种商品时,每件可获利40元;按标价的八折销售该商品5件与将标价降低30元销售该商品3件所获得的利润相等.求该商品每件的进价和标价.
解:设该商品每件的进价为x元,标价为y元.
根据题意,得
解得
答:该商品每件的进价和标价分别是130 元、170元.
4.在某体育用品商店购买50根跳绳和80个毽子共需1120元,购买30根跳绳和50个毽子共需680元.
(1)跳绳、 毽子的单价各是多少元
(2)在“元旦”期间,该店开展促销活动,所有商品按同样的折扣打折销售,若购买100 根跳绳和100个毽子只需1700元,则该店的商品按原价的几折进行销售
解:(1)设跳绳的单价为x元,毽子的单价为y元.
依题意,得
解得
答:跳绳的单价为16元,毽子的单价为4元.
(2)设该店的商品按原价的m折进行销售.
依题意,得16×100+4××100=1700,
解得 m=8.5.
答:该店的商品按原价的八五折进行销售.
利用二元一次方程组进行决策
重点
例3.某生态柑橘园现有柑橘21吨,计划租用A、B两种型号的货车将柑橘运往外地销售.已知满载时,用3辆A型车和2辆B型车一次可运柑橘13吨;用4辆A型车和3辆B型车一次可运柑橘18吨.
(1)1辆A型车和1辆B型车满载时,一次分别运柑橘多少吨
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案.
利用二元一次方程组进行决策
重点
(1)1辆A型车和1辆B型车满载时,一次分别运柑橘多少吨
解:设满载时1辆A型车一次可运柑橘x吨,1辆B型车一次可运柑橘y吨.
依题意,得
解得
答:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨.
利用二元一次方程组进行决策
重点
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案.
解:依题意,得3m+2n=21,∴m=7-n.
又∵m,n均为非负整数,
∴或或或
答:共有4种租车方案.
方案1:租用1辆A型车,9辆B型车;
方案2:租用3辆A型车,6辆B型车;
方案3:租用5辆A型车,3辆B型车;
方案4:只租用7辆A型车.
1.某中学组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车租金为每辆220元,60座客车租金为每辆300元.
(1)这批学生的人数是多少 原计划租用45座客车多少辆
解:设这批学生的人数是x,原计划租用45座客车y辆.
根据题意,得
解得
答:这批学生的人数为240,原计划租用45座客车5辆.
(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用才合算
解:租45座客车:240÷45≈5.3(辆),
所以需租6辆,租金为220×6=1320(元);
租60座客车: 240÷60=4(辆),
所以需租4辆,租金为300×4=1200(元).
因为1200<1320,所以租用4辆60座客车才合算.
答:租用4辆60座客车才合算.
2.妈妈去超市买牙刷和牙膏,已知购买4支牙刷和2盒牙膏需付68元;购买10支牙刷和7盒牙膏需付210元.
(1)求牙刷和牙膏的单价;
解:设牙刷的单价为x元,牙膏的单价为y元.
依题意得
解得
答:牙刷的单价为7元,牙膏的单价为20元.
(2)正好赶上甲、乙两个超市打折优惠,两个超市的每个物品的原价均相同.甲超市:牙刷打九折,牙膏打八折;乙超市:每购买满10盒牙膏送3支牙刷.如果妈妈打算买13 盒牙膏和18支牙刷,那么去哪家超市比较划算 并说明理由.
解:去甲超市比较划算.理由如下:
在甲超市购买所需费用为18×7×0.9+13×20×0.8=321.4(元);
在乙超市购买所需费用为13×20+(18-3)×7=365(元).
∵365>321.4,
∴去甲超市比较划算.
