第6章 实数(复习课件)-2023-2024学年七年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 第6章 实数(复习课件)-2023-2024学年七年级数学下册同步精品课堂(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-22 10:10:04 | ||
图片预览








文档简介
(共22张PPT)
第6章实数复习与小结
人教版数学七年级下册
1.了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、算术平方根、立方根;
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根;
3.了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值;
4.能用有理数估计一个无理数的大致范围.
复习目标
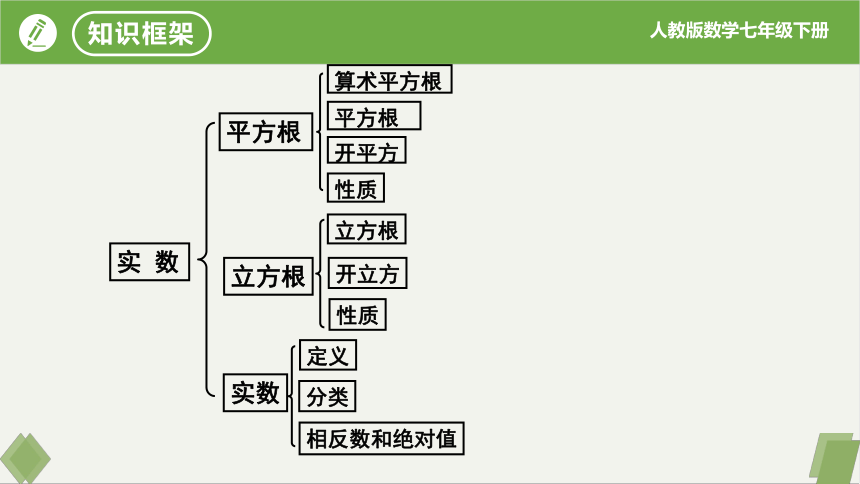
平方根
立方根
定义
开平方
实数
算术平方根
平方根
性质
立方根
开立方
性质
分类
相反数和绝对值
实 数
知识框架
知识点一 平方根的定义和性质
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根. a的算术平方根记为 ,读作“根号a”,a叫做被开方数.
算术平方根:
0的算术平方根是0.
中的双重非负性:
a≥0
知识梳理
平方根的性质:
平方根的概念:
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
知识点一 平方根的定义和性质
知识梳理
知识点二 立方根的定义和性质
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0;
.
=
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
立方根的性质:
立方根的概念:
知识梳理
知识点三 实数的定义和分类
实数的分类:
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
有理数和无理数统称为实数.
知识梳理
1.在-7.5, , 4, , , ,中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
B
随堂检测
2.实数a,b在数轴上的对应点的位置如图6-J-1所示,则正确的结论是 ( )
A. a>-2 B. a<-3
C. a>-b D. a<-b
D
随堂检测
3.下列说法中错误的是( )
A.是的一个平方根
B.正数的两个平方根的和为
C.的平方根是
D.当时,没有平方根
C
随堂检测
4.有理数,,在数轴上的对应点的位置如图所示,则正确的结论是
A. B. C. D.
B
随堂检测
5.下列说法中,不正确的有
任何数都有算术平方根;
一个数的算术平方根一定是正数;
的算术平方根是;
的算术平方根是;
算术平方根不可能是负数,
A. 个 B. 个 C. 个 D. 个
B
随堂检测
6.下列各数:
① 3.141 ② 0.333 33…… ③
④π ⑤ ⑥ ⑦ 0.303 000 300 000 3……(相邻两个3之间0的个数逐次增加2).其中是有理数的有__________,是无理数的有________(填序号).
①②⑤⑥
③④⑦
随堂检测
7.如图所示,数轴上与1, 对应的点分别是为A、B,点B关于点A的对称点为C,设点C表示的数为x,则 = .
0
1
2
B
C
A
随堂检测
8.计算
(1) (2)
=60
=y-1
随堂检测
9.求下列各式的值:
解:① 20; ② ;③ ;④ .
随堂检测
随堂检测
10.计算
解:原式=4+(-3)+3-3
=2+3
11.若
求-ab的平方根.
解:∵|3a+4|≥0且(4b-3)2≥0
且|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a= ,b= .
∴-ab=-( × )=1 ,
∴1的平方根是±1.
随堂检测
12.一个数的算术平方根为2-6,它的平方根为,求这个数.
解:因为一个数的算术平方根为2-6,它的平方根为
①;解得,
(舍去);
②;解得,
所以这个数为.
随堂检测
谢谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第6章实数复习与小结
人教版数学七年级下册
1.了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、算术平方根、立方根;
2.了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根;
3.了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值;
4.能用有理数估计一个无理数的大致范围.
复习目标
平方根
立方根
定义
开平方
实数
算术平方根
平方根
性质
立方根
开立方
性质
分类
相反数和绝对值
实 数
知识框架
知识点一 平方根的定义和性质
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根. a的算术平方根记为 ,读作“根号a”,a叫做被开方数.
算术平方根:
0的算术平方根是0.
中的双重非负性:
a≥0
知识梳理
平方根的性质:
平方根的概念:
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
知识点一 平方根的定义和性质
知识梳理
知识点二 立方根的定义和性质
正数的立方根是正数,
负数的立方根是负数;
0的立方根是0;
.
=
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
立方根的性质:
立方根的概念:
知识梳理
知识点三 实数的定义和分类
实数的分类:
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
有理数和无理数统称为实数.
知识梳理
1.在-7.5, , 4, , , ,中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
B
随堂检测
2.实数a,b在数轴上的对应点的位置如图6-J-1所示,则正确的结论是 ( )
A. a>-2 B. a<-3
C. a>-b D. a<-b
D
随堂检测
3.下列说法中错误的是( )
A.是的一个平方根
B.正数的两个平方根的和为
C.的平方根是
D.当时,没有平方根
C
随堂检测
4.有理数,,在数轴上的对应点的位置如图所示,则正确的结论是
A. B. C. D.
B
随堂检测
5.下列说法中,不正确的有
任何数都有算术平方根;
一个数的算术平方根一定是正数;
的算术平方根是;
的算术平方根是;
算术平方根不可能是负数,
A. 个 B. 个 C. 个 D. 个
B
随堂检测
6.下列各数:
① 3.141 ② 0.333 33…… ③
④π ⑤ ⑥ ⑦ 0.303 000 300 000 3……(相邻两个3之间0的个数逐次增加2).其中是有理数的有__________,是无理数的有________(填序号).
①②⑤⑥
③④⑦
随堂检测
7.如图所示,数轴上与1, 对应的点分别是为A、B,点B关于点A的对称点为C,设点C表示的数为x,则 = .
0
1
2
B
C
A
随堂检测
8.计算
(1) (2)
=60
=y-1
随堂检测
9.求下列各式的值:
解:① 20; ② ;③ ;④ .
随堂检测
随堂检测
10.计算
解:原式=4+(-3)+3-3
=2+3
11.若
求-ab的平方根.
解:∵|3a+4|≥0且(4b-3)2≥0
且|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a= ,b= .
∴-ab=-( × )=1 ,
∴1的平方根是±1.
随堂检测
12.一个数的算术平方根为2-6,它的平方根为,求这个数.
解:因为一个数的算术平方根为2-6,它的平方根为
①;解得,
(舍去);
②;解得,
所以这个数为.
随堂检测
谢谢聆听
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
