2023—2024学年华东师大版数学七年级下册第7章一次方程组培优突破练习(含解析)
文档属性
| 名称 | 2023—2024学年华东师大版数学七年级下册第7章一次方程组培优突破练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 12:20:24 | ||
图片预览




文档简介
第7章 一次方程组
培优突破练习【10个考点50题专练】
2023 2024学年华东师大版数学七年级下册
一.二元一次方程的解(共4小题)
1.(2023秋 紫金县期末)已知和是二元一次方程的两个解,则,的值分别为
A.2, B.,1 C.,2 D.1,
2.(2023 南岗区校级开学)已知是方程的一个解,那么的值为
A. B.2 C.3 D.6
3.(2023 西山区校级开学)二元一次方程的正整数解有
A.1组 B.2组 C.3组 D.4组
4.(2023春 霸州市期末)已知关于,的二元一次方程●中的系数让墨迹盖住了,但是知道它一组解是,那么●的值是
A.2 B.1 C. D.
二.解二元一次方程(共2小题)
5.(2023秋 三元区期末)把方程变形,用含的代数式表示,则 .
6.(2023秋 东港区期中)如果把方程写成用含的代数式表示的形式,那么 .
三.由实际问题抽象出二元一次方程(共1小题)
7.(2023秋 高碑店市期末)某校为了培养学生阅读的习惯,准备把一批课外书分给学生阅读,一共有名学生,本课外书,若每名学生发3本,则少3本课外书;若每名学生发2本,则多9本课外书.有下列4个方程:①;②;③;④.其中符合题意的是
A.②③ B.①③ C.②④ D.①④
四.二元一次方程的应用(共3小题)
8.(2022秋 城口县校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大45,这样的两位数共有
A.2个 B.3个 C.4个 D.5个
9.(2023秋 城关区校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 个.
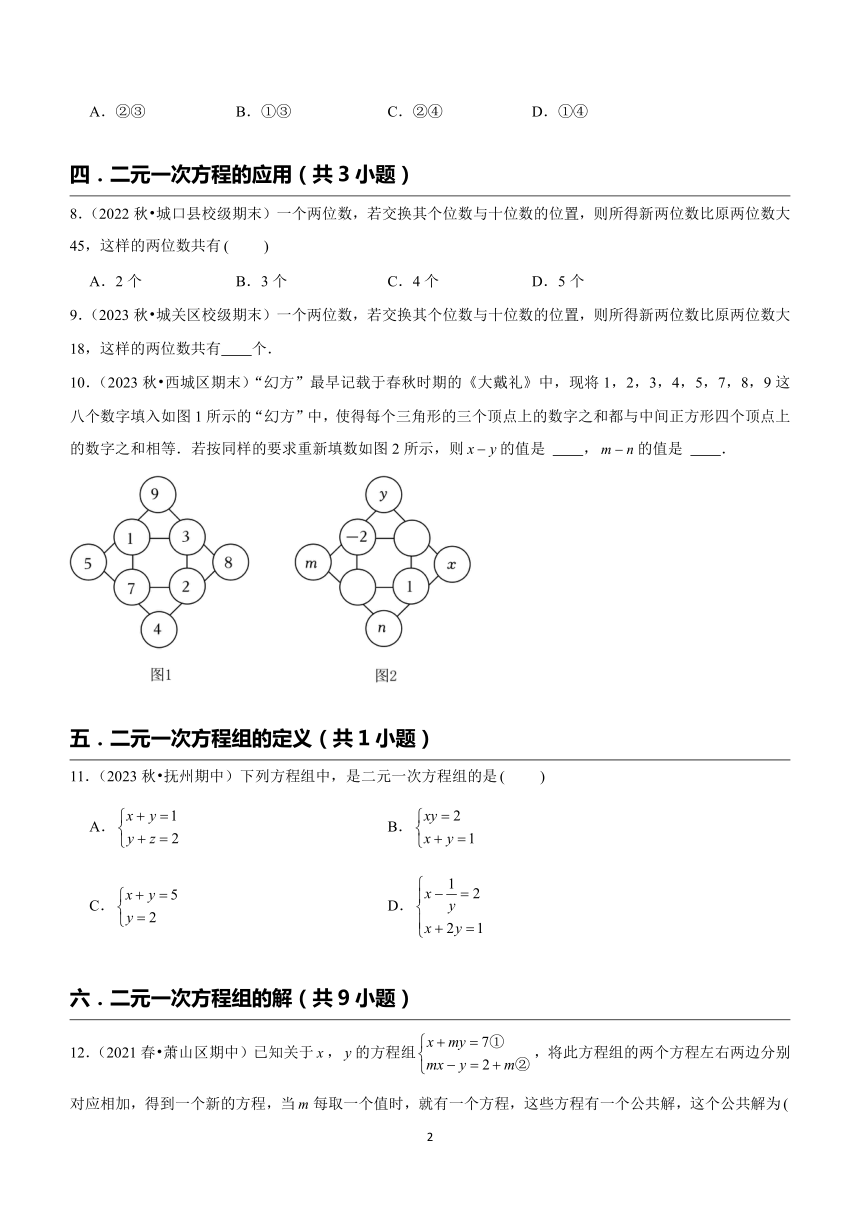
10.(2023秋 西城区期末)“幻方”最早记载于春秋时期的《大戴礼》中,现将1,2,3,4,5,7,8,9这八个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.若按同样的要求重新填数如图2所示,则的值是 ,的值是 .
五.二元一次方程组的定义(共1小题)
11.(2023秋 抚州期中)下列方程组中,是二元一次方程组的是
A. B.
C. D.
六.二元一次方程组的解(共9小题)
12.(2021春 萧山区期中)已知关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为
A. B. C. D.
13.(2023春 内江期末)关于、的二元一次方程组的解是二元一次方程的一个解,则的值是
A. B. C.2 D.4
14.(2022秋 青羊区校级期末)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为 .
15.(2023春 吴兴区校级期末)关于,的二元一次方程组的解满足,则的值是 .
16.(2022春 合浦县期中)方程组的解满足是常数),
(1)求的值.
(2)直接写出关于,的方程的正整数解
17.(2021春 沙依巴克区校级期中)已知关于,的方程组.
(1)请写出方程的所有正整数的解;
(2)若方程组的解满足,求的值.
(3)无论实数取何值,方程总有一个公共解,你能求出这个公共解吗?
(4)如果方程组有整数解,求整数的值.
18.(2021春 江阴市校级月考)已知关于,的方程组与的解相同,求,的值.
19.(2023春 沈丘县月考)已知关于,的方程组,
(1)若方程组的解满足方程,求的值;
(2)请你给出的一个值,使方程组的解中,都是正整数,并直接写出方程组的解.
20.(2021春 松桃县期末)解关于的方程组时,甲正确解出,乙因把抄错了,误解为,求、、的值.
七.解二元一次方程组(共4小题)
21.(2012春 华容县期末)已知,则的值为
A . B . C . 1 D .
22.(2022秋 文山市期末)方程组的解是
A. B. C. D.
23.(2022秋 冷水滩区期中)对于实数,规定新运算:,其中、是常数.已知,.
(1)求、的值;
(2)求的值.
24.(2022春 仁化县期中)已知关于,的二元一次方程的解有和.
(1)求,的值.
(2)当时,的值.
(3)当为何值时,?
八.由实际问题抽象出二元一次方程组(共5小题)
25.(2023秋 萧县期末)《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问:几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问:多久后甲、乙相逢?设甲出发日,乙出发日后甲、乙相逢,则所列方程组正确的是
A. B.
C. D.
26.(2023 南山区校级三模)某校劳动课学习制作娃娃和沙包,已知每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物.布料没有剩余,礼物也恰好成套.设做娃娃用了米布,做沙包用了米布,则
A. B.
C. D.
27.(2022秋 祥符区期末)端午节前夕,某超市用1680元购进、两种商品共60件,其中型商品每件24元,型商品每件36元.设购买型商品件、型商品件,依题意列方程组正确的是
A. B.
C. D.
28.(2023 定海区模拟)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是
A. B.
C. D.
29.(2023 二道区校级模拟)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为 .
九.二元一次方程组的应用(共16小题)
30.(2023秋 香坊区校级期中)某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,问应该分配 名工人生产螺栓,才能使当天的螺栓和螺母刚好配套?
A.13 B.14 C.15 D.16
31.(2022秋 翁源县期末)2022年卡塔尔世界杯欧洲区预选赛中,某国家队参加了10场比赛,仅负1场,共积23分,按比赛规则,胜一场得3分,平一场得1分,负一场得0分,则该队共胜了 场
A.4 B.5 C.6 D.7
32.(2023 蕉岭县一模)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出十一,盈八;人出九,不足十二.问物价几何?译文为:现有一些人共同买一个物品,每人出11元,还盈余8元;每人出9元,则还差12元.问这个物品的价格是多少元?
A.118 B.102 C.88 D.78
33.(2023春 霸州市期末)有这样一道数学题:只闻隔壁人分银,不知多少银和人,每人半斤多半斤,每人九两少一两,试问各位善算者,多少人分多少银?其大意为有一群人分若干两银子,如果每人分半斤,则剩半斤,如果每人分9两,则少1两,问多少人分多少两银子?(注这里的斤是指市斤,1市斤两)
A.9人,64两 B.9人,80两 C.10人,89两 D.10人,85两
34.(2023 碑林区校级开学)《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五:人出八,不足三.问人数几何?”题意是:若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.则买羊的人有 个.
35.(2023秋 沈河区期末)在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为 .
36.(2022秋 太原期末)兔年春节之际,小文和几个同学要用自己的压岁钱为社区敬老院购买春节礼品,如果每人出80元,那么可剩余36元;如果每人出70元,那么还差14元.参加此次活动的共有 人.
37.(2023秋 松江区期末)如图,在大长方形中,放入8个一样形状和大小的小长方形,则图中阴影部分面积为 平方厘米.
38.(2023 栾城区校级开学)用白铁皮制作罐头盒,每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮,用 张制作盒身, 张制作盒底,能使盒身和盒底恰好配套.
39.(2022春 忠县校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某公司有31吨货物,计划同时租用型车辆,型车辆,一次运完,且每辆车都装满货物.根据以上信息解答下列问题:
(1)一辆型车和一辆型车装满货物一次各运多少吨?
(2)请你帮公司设计租车方案.
(3)若型车每辆租金100元,型车每辆租金120元,哪种方案租金最少?
40.(2021秋 驻马店期末)医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
41.(2022春 霍林郭勒市校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某物流公司现有36吨货物,计划同时租用型车辆,型车辆,(要求既有型车又有型车)一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆型车和1辆型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
42.(2022春 海丰县期末)温州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 套(含39套) 套(含79套) 80套及以上
每套服装的价格 80元 70元 60元
经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,两个乐团共需花费5600元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调人,从乙乐团抽调人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
43.(2023秋 萧县期末)两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数,已知前一个四位数比后一个四位数大2178,求这两个两位数.
44.(2021 安徽模拟)甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价,乙商品提价,调价后,两种商品的单价和比原来的单价和提高了.问甲、乙两种商品原来的单价各是多少元?
45.(2023春 江源区期末)如图,宽为长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少?
一十.三元一次方程组的应用(共5小题)
46.(2023 武汉模拟)在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为,其内部的格点数记为,边界上的格点数记为,例如,图中的是格点三角形,其中,,;图中格点多边形所对应的,,分别是,,.经探究发现,任意格点多边形的面积可表示为,其中,,为常数,则当,时,的值为
A.44 B.43 C.100 D.99
47.(2023 沙坪坝区校级开学)传统文化中,橙子和柿子都是带有美好寓意的水果.今年春节,津南果品店就推出了由奉节脐橙和城口磨盘柿组成的甲、乙、丙、丁四种礼盒,其中甲礼盒有1千克脐橙,乙礼盒有1千克磨盘柿,丙礼盒有2千克脐橙和1千克磨盘柿.丁礼盒有以1千克脐橙和2千克磨盘柿.每种礼盒的售价为所含果品的售价之和,两种果品每千克的售价均为整数(磨盘柿比脐橙贵),且每千克的售价之和介于30元与40元之间.第一天试销,甲、乙、丙、丁四种礼盒的销售数量之比为.第二天果品店将甲礼盒改为2千克脐橙,乙礼盒改为2千克磨盘柿.丙礼盒改为9千克脐橙和6千克磨盘柿.丁礼盒改为6千克脐橙和8千克磨盘柿.当天甲、丙、丁这三种含有脐橙的礼盒销售数量之比为.且这三种礼盒的销售总额比第一天四种礼盒的销售总额少6410元.而乙礼盒销售数量则为第一天的,从果品种类统计发现,这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,则这两天甲礼盒的总销售额为 .
48.(2023春 温州月考)购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
49.(2023春 渝中区校级月考)为方便居家期间生活,生鲜超市为某小区业主准备了、、三种类型的蔬菜包销售(整包销售).第一天销售时,蔬菜包的售价为每包32元,利润率为,蔬菜包成本为每包36元,每包提价14元销售,蔬菜包每包的成本是蔬菜包每包成本的,售价为每包60元,且蔬菜包的销售数量不少于20包,第一天将所有准备的蔬菜包全部销售完后,三种蔬菜包的销售总额为4016元,其中、两种蔬菜包的销售利润共826元.第二天生鲜超市准备的、、三种蔬菜包的数量和第一天完全相同,而蔬菜包的成本增加了,售价不变,蔬菜包的成本不变,利润率变为,蔬菜包的成本和售价均保持不变,但在运送过程中蔬菜包的损坏无法销售,则第二天三种蔬菜包销售完后的总利润为 元.
50.(2021秋 绵阳期末)有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:
总积分
9
7
(1)某球队要取得一场比赛的胜利,可能的比分结果是什么?
(2)若比分为时,净胜球为2,比分为时,净胜球为1,依此类推,净胜球越多,积分也越多.请你根据表格中的数据,求出各种比分对应的积分分别是什么?
(3)在(2)的条件下,若球队战胜了球队,但总积分,求,的值.
答案解析
一.二元一次方程的解(共4小题)
1.(2023秋 紫金县期末)已知和是二元一次方程的两个解,则,的值分别为
A.2, B.,1 C.,2 D.1,
【答案】
【分析】把方程组的解代入方程组,得出关于、的方程组,解方程组即可.
【解答】解:和是二元一次方程的两个解,
,
①②,得,,
,
故选:.
2.(2023 南岗区校级开学)已知是方程的一个解,那么的值为
A. B.2 C.3 D.6
【答案】
【分析】把,代入方程得出方程,求的值即可.
【解答】解:,是方程的一个解,
,
解得:,
故选:.
3.(2023 西山区校级开学)二元一次方程的正整数解有
A.1组 B.2组 C.3组 D.4组
【答案】
【分析】用含的式子表示出,求出所有的正整数解即可得出答案.
【解答】解:由得:,
当时,;
当时,;
当时,;
二元一次方程的正整数解有3组,
故选:.
4.(2023春 霸州市期末)已知关于,的二元一次方程●中的系数让墨迹盖住了,但是知道它一组解是,那么●的值是
A.2 B.1 C. D.
【答案】
【分析】根据方程解的意义列方程求解.
【解答】解:设,
由题意得:,
解得:,
故选:.
二.解二元一次方程(共2小题)
5.(2023秋 三元区期末)把方程变形,用含的代数式表示,则 .
【答案】.
【分析】移项即可.
【解答】解:移项得,,
故答案为:.
6.(2023秋 东港区期中)如果把方程写成用含的代数式表示的形式,那么 .
【答案】.
【分析】将方程移项即可.
【解答】解:由可得:.
故答案为:.
三.由实际问题抽象出二元一次方程(共1小题)
7.(2023秋 高碑店市期末)某校为了培养学生阅读的习惯,准备把一批课外书分给学生阅读,一共有名学生,本课外书,若每名学生发3本,则少3本课外书;若每名学生发2本,则多9本课外书.有下列4个方程:①;②;③;④.其中符合题意的是
A.②③ B.①③ C.②④ D.①④
【答案】
【分析】分别根据书的总量相等和学生的人数相等列出方程即可.
【解答】解:根据书的数量相等可列方程为,根据学生的人数相等可列方程为,
所以符合题意的是①④.
故选:.
四.二元一次方程的应用(共3小题)
8.(2022秋 城口县校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大45,这样的两位数共有
A.2个 B.3个 C.4个 D.5个
【答案】
【分析】设原两位数的十位数字为,且为整数),个位数字为,且为整数),则原两位数可表示为,新两位数可表示为,根据题意得出,整理得,再进一步求解即可.
【解答】解:设原两位数的十位数字为,且为整数),个位数字为,且为整数),
则原两位数可表示为,新两位数可表示为,
根据题意,得:,
整理,得:,
当时,,此时两位数为49,
当时,,此时两位数为38,
当时,,此时两位数为27,
当时,,此时两位数为16,
故选:.
9.(2023秋 城关区校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 7 个.
【答案】7.
【分析】先设原来的两位数为,根据交换其个位数与十位数的位置,所得新两位数比原两位数大18,列出方程,得出,因此可取1到8个数,并且这8个数的特点都是个位数字比十位数字大2的两位数.
【解答】解:设原来的两位数为,
根据题意可得:
,
解得:,
可取从3到9的所有自然数,
即3、4、5、6、7、8、9,
这样的两位数共有7个,
它们分别是13,24,35,46,57,68,79.
故答案为:7.
10.(2023秋 西城区期末)“幻方”最早记载于春秋时期的《大戴礼》中,现将1,2,3,4,5,7,8,9这八个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.若按同样的要求重新填数如图2所示,则的值是 ,的值是 .
【答案】,3.
【分析】根据每个三角形的三个顶点上的数字之和相等,得,,即可得出结论.
【解答】解:根据题意得:,,
,,
故答案为:,3.
五.二元一次方程组的定义(共1小题)
11.(2023秋 抚州期中)下列方程组中,是二元一次方程组的是
A. B.
C. D.
【答案】
【分析】利用二元一次方程组的定义逐一分析各选项中的方程,即可得出结论.
【解答】解:.方程组含有三个未知数,
方程组不是二元一次方程组,选项不符合题意;
.方程组中方程是二次方程,
方程组不是二元一次方程组,选项不符合题意;
.方程组是二元一次方程组,选项符合题意;
.方程组中方程不是整式方程,
方程组不是二元一次方程组,选项不符合题意.
故选:.
六.二元一次方程组的解(共9小题)
12.(2021春 萧山区期中)已知关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为
A. B. C. D.
【答案】
【分析】根据题意①②得,然后根据题意列出方程组即可求得公共解.
【解答】解:①②得,
根据题意,这些方程有一个公共解,与的取值无关,
解得
所以这个公共解为
故选:.
13.(2023春 内江期末)关于、的二元一次方程组的解是二元一次方程的一个解,则的值是
A. B. C.2 D.4
【答案】
【分析】先利用加减消元法解方程组得到方程组的解为,再把代入方程中求出的值即可.
【解答】解:
①②得:,解得,
把代入①得:,解得,
方程组的解为,
关于、的二元一次方程组的解是二元一次方程的一个解,
,
,
故选:.
14.(2022秋 青羊区校级期末)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为 4 .
【答案】4.
【分析】求方程组的解,将它代入方程,求出的值即可.
【解答】解:解方程组,得,
将代入方程,得,解得.
故答案为:4.
15.(2023春 吴兴区校级期末)关于,的二元一次方程组的解满足,则的值是 .
【答案】.
【分析】将两式相加,得到,然后得到,据此即可求解.
【解答】解:,
由②①得,
,
,
,
解得.
故答案为:.
16.(2022春 合浦县期中)方程组的解满足是常数),
(1)求的值.
(2)直接写出关于,的方程的正整数解
【分析】(1)先求出方程组的解,再代入方程,即可求出值;
(2)把的值代入方程,再求出正整数解即可.
【解答】解:(1)方程组的解为:,
将代入得:,
解得:;
(2)把代入方程得:,
即,
所以关于,的方程的正整数解为,.
17.(2021春 沙依巴克区校级期中)已知关于,的方程组.
(1)请写出方程的所有正整数的解;
(2)若方程组的解满足,求的值.
(3)无论实数取何值,方程总有一个公共解,你能求出这个公共解吗?
(4)如果方程组有整数解,求整数的值.
【答案】(1),;
(2);
(3);
(4)或2.
【分析】(1)把看作已知数表示出,进而确定出方程的正整数解即可;
(2)已知方程与方程组第一个方程联立求出与的值,进而求出的值;
(3)方程变形后,确定出公共解即可;
(4)根据方程组有整数解,确定出整数的值即可.
【解答】解:(1)方程,
解得:,
当时,;,;
即方程的正整数的解为,;
(2)联立得,
解得,
代入得:,
解得;
(3),即总有一个解,
方程的解与无关,
,,
解得:,,
则方程的公共解为;
(4),
①②得:,
解得:,
把代入①得:,
当,1,,,4,时,为整数,此时.,,,2,,
当时,,不符合题意;
当时,,不符合题意;
当时,,符合题意;
当时,,符合题意,
当时,,不符合题意;
当时,,不符合题意,
综上所述,整数的值为或2.
18.(2021春 江阴市校级月考)已知关于,的方程组与的解相同,求,的值.
【分析】联立两个方程组中不含与的方程组成方程组,求出解确定出与的值即可.
【解答】解:联立得:,
①②得:,即,
把代入①得:,
把,代入得:,
解得:,.
19.(2023春 沈丘县月考)已知关于,的方程组,
(1)若方程组的解满足方程,求的值;
(2)请你给出的一个值,使方程组的解中,都是正整数,并直接写出方程组的解.
【分析】(1)由方程组解出、,再代入即可解决问题.
(2)是大于3的整数,任意取一个值即可.
【解答】解:(1)由,解得
把,代入,得
.
(2),则,.(答案不唯一).
20.(2021春 松桃县期末)解关于的方程组时,甲正确解出,乙因把抄错了,误解为,求、、的值.
【分析】把甲的解代入方程组,乙因把抄错了,方程组中第一个方程不含,把乙的解代入方程组中第一个方程,列三元一次方程组求、、的值.
【解答】解:依题意,得,
③①得,解得,
把代入③,得,
由②得,
所以,,,.
七.解二元一次方程组(共4小题)
21.(2012春 华容县期末)已知,则的值为
A . B . C . 1 D .
【分析】利用非负数的性质列出关于与的方程组, 求出方程组的解得到与的值, 即可求出所求式子的值 .
【解答】解:,
,
①②得:,即,
将代入①得:,即,
则原式.
故选:.
22.(2022秋 文山市期末)方程组的解是
A. B. C. D.
【答案】
【分析】根据代入消元法求解.
【解答】解:由第二个方程得:③,
把③代入第一个方程得:,
解得:,
把代入③得:,
故选:.
23.(2022秋 冷水滩区期中)对于实数,规定新运算:,其中、是常数.已知,.
(1)求、的值;
(2)求的值.
【分析】(1)利用新定义和两组对应值得到,然后利用加减法解方程组即可;
(2)由(1)得新运算为:,然后把,代入计算即可.
【解答】解:(1)根据题意得,
解得,;
(2)由(1)得,
所以.
24.(2022春 仁化县期中)已知关于,的二元一次方程的解有和.
(1)求,的值.
(2)当时,的值.
(3)当为何值时,?
【分析】(1)将两组,的值代入方程得出关于、的二元一次方程组,再运用加减消元法求出、的值.
(2)将(1)中的、代入,再把代入化简即可得出的值.
(3)将(1)中的、和代入方程化简即可得出的值.
【解答】解:
(1)依题意得:
①②得:,
所以,
所以.
(2)由,
把代入,得.
(3)由
把代入,得.
八.由实际问题抽象出二元一次方程组(共5小题)
25.(2023秋 萧县期末)《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问:几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问:多久后甲、乙相逢?设甲出发日,乙出发日后甲、乙相逢,则所列方程组正确的是
A. B.
C. D.
【答案】
【分析】可将此题看作是工作效率类的应用题,根据效率时间总量列方程即可.
【解答】解:由题可知,甲的效率为,乙的效率为,
设甲出发日,乙出发日后甲、乙相逢,根据题意列方程组:
.
故选:.
26.(2023 南山区校级三模)某校劳动课学习制作娃娃和沙包,已知每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物.布料没有剩余,礼物也恰好成套.设做娃娃用了米布,做沙包用了米布,则
A. B.
C. D.
【答案】
【分析】根据“每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物”,即可得出关于,的二元一次方程组,此题得解.
【解答】解:依题意得:.
故选:.
27.(2022秋 祥符区期末)端午节前夕,某超市用1680元购进、两种商品共60件,其中型商品每件24元,型商品每件36元.设购买型商品件、型商品件,依题意列方程组正确的是
A. B.
C. D.
【答案】
【分析】根据题意,由超市用1680元购进,两种商品,结合两种商品的单价可得到一个方程;再由,两种商品共60件得到另一个方程,联立即可得到答案.
【解答】解:由题意得:,
,
.
故选:.
28.(2023 定海区模拟)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是
A. B.
C. D.
【答案】
【分析】根据“人数物品价值、物品价值人数”可得方程组.
【解答】解:若设有人,物品价值元,根据题意,可列方程组为,
故选:.
29.(2023 二道区校级模拟)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为 .
【分析】设大马有匹,小马有匹,由题意得等量关系:①共有马100匹;②大马拉瓦数小马拉瓦数,根据等量关系,列出方程组即可.
【解答】解:设大马有匹,小马有匹,由题意得:
,
故答案为:.
九.二元一次方程组的应用(共16小题)
30.(2023秋 香坊区校级期中)某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,问应该分配 名工人生产螺栓,才能使当天的螺栓和螺母刚好配套?
A.13 B.14 C.15 D.16
【答案】
【分析】设应该分配名工人生产螺栓,人生产螺母,才能使当天的螺栓和螺母刚好配套,根据某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,列出二元一次方程组,解方程组即可.
【解答】解:设应该分配名工人生产螺栓,人生产螺母,才能使当天的螺栓和螺母刚好配套,
由题意得:,
解得:,
即应该分配15名工人生产螺栓,20人生产螺母,才能使当天的螺栓和螺母刚好配套,
故选:.
31.(2022秋 翁源县期末)2022年卡塔尔世界杯欧洲区预选赛中,某国家队参加了10场比赛,仅负1场,共积23分,按比赛规则,胜一场得3分,平一场得1分,负一场得0分,则该队共胜了 场
A.4 B.5 C.6 D.7
【答案】
【分析】设该队共胜场,则平场,由题意知,,计算求解即可.
【解答】解:设该队共胜场,则平场,
由题意知,,
解得,
该队共胜7场,
故选:.
32.(2023 蕉岭县一模)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出十一,盈八;人出九,不足十二.问物价几何?译文为:现有一些人共同买一个物品,每人出11元,还盈余8元;每人出9元,则还差12元.问这个物品的价格是多少元?
A.118 B.102 C.88 D.78
【答案】
【分析】设共有人,这个物品的价格是元,根据每人出11元,还盈余8元;每人出9元,则还差12元.列出二元一次方程组,解方程组即可.
【解答】解:设共有人,这个物品的价格是元,
由题意得:,
解得:,
即这个物品的价格是102元,
故选:.
33.(2023春 霸州市期末)有这样一道数学题:只闻隔壁人分银,不知多少银和人,每人半斤多半斤,每人九两少一两,试问各位善算者,多少人分多少银?其大意为有一群人分若干两银子,如果每人分半斤,则剩半斤,如果每人分9两,则少1两,问多少人分多少两银子?(注这里的斤是指市斤,1市斤两)
A.9人,64两 B.9人,80两 C.10人,89两 D.10人,85两
【答案】
【分析】设有个人,共分两银子,根据如果每人分半斤,则剩半斤,如果每人分9两,则少1两,列出二元一次方程组,解方程组即可.
【解答】解:设有个人,共分两银子,
根据题意得:,
解得:,
即有9个人,共分80两银子,
故选:.
34.(2023 碑林区校级开学)《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五:人出八,不足三.问人数几何?”题意是:若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.则买羊的人有 21 个.
【答案】21.
【分析】设买羊的人有个,羊价为元,根据若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.列出二元一次方程组,解方程组即可.
【解答】解:设买羊的人有个,羊价为元,
由题意得:,
解得:,
即买羊的人有21个,
故答案为:21.
35.(2023秋 沈河区期末)在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为 27 .
【答案】27.
【分析】设小长方形的长为 ,宽为 ,根据图形中大长方形的长和宽列二元一次方程组,解方程组,即可解决问题.
【解答】解:设小长方形的长为 ,宽为 ,
根据题意得:,
解得:,
,
即每个小长方形的面积为,
阴影部分的面积,
故答案为:27.
36.(2022秋 太原期末)兔年春节之际,小文和几个同学要用自己的压岁钱为社区敬老院购买春节礼品,如果每人出80元,那么可剩余36元;如果每人出70元,那么还差14元.参加此次活动的共有 5 人.
【答案】5.
【分析】设此次参加活动的共有人,根据购买春节礼品的总钱数不变,可得方程,解之即可.
【解答】解:设此次参加活动的共有人,
由题意可得:,
解得:,
此次参加活动的共有5人,
故答案为:5.
37.(2023秋 松江区期末)如图,在大长方形中,放入8个一样形状和大小的小长方形,则图中阴影部分面积为 92 平方厘米.
【答案】92.
【分析】根据图中的数据,可以列出相应的二元一次方程组,然后即可求得小长方形的长和宽,然后即可计算出图中阴影部分的面积.
【解答】解:设小长方形的长为 ,宽为 ,
由图可得:,
解得,
图中阴影部分的面积为:
(平方厘米),
故答案为:92.
38.(2023 栾城区校级开学)用白铁皮制作罐头盒,每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮,用 20 张制作盒身, 张制作盒底,能使盒身和盒底恰好配套.
【答案】20,16.
【分析】设用张制作盒身,张制作盒底,由“每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮”,列出二元一次方程组,解方程组即可.
【解答】解:设用张制作盒身,张制作盒底,
由题意得:,
解得:,
用20张制作盒身,16张制作盒底,
故答案为:20,16.
39.(2022春 忠县校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某公司有31吨货物,计划同时租用型车辆,型车辆,一次运完,且每辆车都装满货物.根据以上信息解答下列问题:
(1)一辆型车和一辆型车装满货物一次各运多少吨?
(2)请你帮公司设计租车方案.
(3)若型车每辆租金100元,型车每辆租金120元,哪种方案租金最少?
【答案】(1)1辆型车装满货物一次可运货3吨,1辆型车装满货物一次可运货4吨;
(2)该物流公司共有3种租车方案,
方案1:租用型车1辆,型车7辆;
方案2:租用型车5辆,型车4辆;
方案3:租用型车9辆,型车1辆;
(3)方案1:租用型车1辆,型车7辆最省钱,最少租车费为940元.
【分析】(1)设1辆型车装满货物一次可运货吨,1辆型车装满货物一次可运货吨,根据“用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨”,即可得出关于,的二元一次方程组,解之即可得出结论;
(2)设租用辆型车,辆型车,根据租用的两种型号车满载货物一次可运货31吨,即可得出关于,的二元一次方程,结合,均为正整数,即可得出各租车方案;
(3)利用总租金每辆车的租金租用该车型数量,可分别求出各租车方案所需租车费,比较后即可得出结论.
【解答】解:(1)设1辆型车装满货物一次可运货吨,1辆型车装满货物一次可运货吨,
依题意得:,
解得:.
答:1辆型车装满货物一次可运货3吨,1辆型车装满货物一次可运货4吨.
(2)设租用辆型车,辆型车,
依题意得:,
.
又,均为正整数,
或或,
该物流公司共有3种租车方案,
方案1:租用型车1辆,型车7辆;
方案2:租用型车5辆,型车4辆;
方案3:租用型车9辆,型车1辆.
(3)租车方案1所需费用(元;
租车方案2所需费用(元;
租车方案3所需费用(元.
,
方案1:租用型车1辆,型车7辆最省钱,最少租车费为940元.
40.(2021秋 驻马店期末)医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
【分析】本题中可将等量关系列为每餐中甲含的蛋白质的量乙含的蛋白质的量,每餐中甲含的铁质的量乙含的铁质的量.由此列出方程组求解.
【解答】解:设每餐需甲原料克,乙原料克,
根据题意可列方程组
解得:.
答:每餐需甲种原料28克,乙种原料30克.
41.(2022春 霍林郭勒市校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某物流公司现有36吨货物,计划同时租用型车辆,型车辆,(要求既有型车又有型车)一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆型车和1辆型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
【答案】(1)1辆型车和1辆型车都装满货物一次可分别运货3吨,4吨;
(2)故共有两种租车方案,分别为:①型车4辆,型车6辆;②型车8辆,型车3辆.
【分析】(1)设1辆型车和1辆型车都装满货物一次可分别运货吨,吨,根据“用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨”,即可得出关于、的二元一次方程组,解之即可得出结论;
(2)由(1)的结论结合某物流公司现有31吨货物,即可得出,即,由、均为正数即可得出各租车方案.
【解答】解:(1)设1辆型车和1辆型车都装满货物一次可分别运货吨,吨,
根据题意得:,
解得:.
答:1辆型车和1辆型车都装满货物一次可分别运货3吨,4吨.
(2)由题意可得:,
.
,均为整数,(要求既有型车又有型车)
有和两种情况.
故共有两种租车方案,分别为:
①型车4辆,型车6辆;
②型车8辆,型车3辆.
42.(2022春 海丰县期末)温州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 套(含39套) 套(含79套) 80套及以上
每套服装的价格 80元 70元 60元
经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,两个乐团共需花费5600元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调人,从乙乐团抽调人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
【分析】(1)若甲、乙两个乐团合起来购买服装80套,则每套是60元,计算出总价,即可求得比各自购买服装共可以节省多少钱;
(2)设甲、乙个乐团各有名、名学生准备参加演出.根据题意,显然各自购买时,甲乐团每套服装是70元,乙乐团每套服装是80元.根据等量关系:①共75人;②分别单独购买服装,一共应付5600元,列方程组即可求解;
(3)利用甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友恰好使得福利院65位小朋友全部得到“心连心活动”的温暖列出方程探讨答案即可.
【解答】解:(1)买80套所花费为:(元,
最多可以节省:(元.
(2)解:设甲乐团有人;乙乐团有人.
根据题意,得
解得
答:甲乐团有40人;乙乐团有35人.
(3)由题意,得
变形,得
因为每位乐团的人数不少于5人且人数为正整数
得:或.
所以共有两种方案:从甲乐团抽调5人,从乙乐团抽调10人;或者从甲乐团抽调10人,从乙乐团抽调7人.
43.(2023秋 萧县期末)两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数,已知前一个四位数比后一个四位数大2178,求这两个两位数.
【分析】首先设较大的两位数为,较小的两位数为,根据题意可得等量关系:①两个两位数的和为68,②比大2178,根据等量关系列出方程组,再解方程组即可.
【解答】解:设较大的两位数为,较小的两位数为,
根据题意,得
,
化简得:,
即,
解得.
答:这两个数是45和23.
44.(2021 安徽模拟)甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价,乙商品提价,调价后,两种商品的单价和比原来的单价和提高了.问甲、乙两种商品原来的单价各是多少元?
【分析】如果设甲商品原来的单价是元,乙商品原来的单价是元,那么根据“甲、乙两种商品原来的单价和为100元”可得出方程为根据“甲商品降价,乙商品提价,调价后,两种商品的单价之和比原来的单价之和提高了”,可得出方程为.
【解答】解:设甲种商品原来的单价是元,乙种商品原来的单价是元,依题意得
,
解得:.
答:甲种商品原来的单价是40元,乙种商品原来的单价是60元.
45.(2023春 江源区期末)如图,宽为长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少?
【分析】本题可以通过看图找出两个等量关系:长方形的长宽,长方形的长长宽,据此可以设未知数列方程组求解.
【解答】解:设每块小长方形的长是,宽是,根据题意得
解得
答:长是,宽是.
一十.三元一次方程组的应用(共5小题)
46.(2023 武汉模拟)在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为,其内部的格点数记为,边界上的格点数记为,例如,图中的是格点三角形,其中,,;图中格点多边形所对应的,,分别是,,.经探究发现,任意格点多边形的面积可表示为,其中,,为常数,则当,时,的值为
A.44 B.43 C.100 D.99
【答案】
【分析】根据格点多边形的面积,结合图中的格点、格点多边形、格点四边形的、、数值,列出三元一次方程组,解方程组,求出、、的值,即可解决问题.
【解答】解:由题意得:四边形是格点四边形,,,,
任意格点多边形的面积,
由图中的格点、格点多边形、格点四边形得:
,
解得:,
,
将,代入得:,
故选:.
47.(2023 沙坪坝区校级开学)传统文化中,橙子和柿子都是带有美好寓意的水果.今年春节,津南果品店就推出了由奉节脐橙和城口磨盘柿组成的甲、乙、丙、丁四种礼盒,其中甲礼盒有1千克脐橙,乙礼盒有1千克磨盘柿,丙礼盒有2千克脐橙和1千克磨盘柿.丁礼盒有以1千克脐橙和2千克磨盘柿.每种礼盒的售价为所含果品的售价之和,两种果品每千克的售价均为整数(磨盘柿比脐橙贵),且每千克的售价之和介于30元与40元之间.第一天试销,甲、乙、丙、丁四种礼盒的销售数量之比为.第二天果品店将甲礼盒改为2千克脐橙,乙礼盒改为2千克磨盘柿.丙礼盒改为9千克脐橙和6千克磨盘柿.丁礼盒改为6千克脐橙和8千克磨盘柿.当天甲、丙、丁这三种含有脐橙的礼盒销售数量之比为.且这三种礼盒的销售总额比第一天四种礼盒的销售总额少6410元.而乙礼盒销售数量则为第一天的,从果品种类统计发现,这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,则这两天甲礼盒的总销售额为 85 .
【答案】85.
【分析】设磨盘柿和脐橙的单价分别为、,第一天甲四种礼盒的销售数量为,第二天甲四种礼盒的销售数量为,再依据题意列出方程和不等式,最后计算即可.
【解答】解:设磨盘柿和脐橙的单价分别为、,第一天甲四种礼盒的销售数量为,第二天甲四种礼盒的销售数量为,
第一天甲、乙、丙、丁四种礼盒的销售数量依次为、、、,
第二天甲、丙、丁这三种含有脐橙的礼盒销售数量依次为、、,乙礼盒销售数量为,
第一天销售磨盘柿千克,脐橙千克,
第二天三种礼盒销售磨盘柿千克,脐橙千克,
这三种礼盒的第二天销售总额比第一天四种礼盒的销售总额少6410元,
,
整理得,
磨盘柿比脐橙贵,且每千克的售价之和介于30元与40元之间,
,,
,
是质数,
,,
,
这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,
,
整理得:,
,
解得,
,,
这两天甲礼盒的总销售额为,
故答案为:85.
48.(2023春 温州月考)购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 7 元.
【答案】7.
【分析】首先假设铅笔的单价是元,作业本的单价是元,中性笔的单价是元.购买铅笔2支,作业本1本,中性笔1支共需元.根据题目说明列出方程组,解方程组求出的值,即为所求结果.
【解答】解:设铅笔的单价是元,作业本的单价是元,中性笔的单价是元.购买铅笔2支,作业本1本,中性笔1支共需元.
则由题意得:
,
由①②得,
于是:,
故答案为:7.
49.(2023春 渝中区校级月考)为方便居家期间生活,生鲜超市为某小区业主准备了、、三种类型的蔬菜包销售(整包销售).第一天销售时,蔬菜包的售价为每包32元,利润率为,蔬菜包成本为每包36元,每包提价14元销售,蔬菜包每包的成本是蔬菜包每包成本的,售价为每包60元,且蔬菜包的销售数量不少于20包,第一天将所有准备的蔬菜包全部销售完后,三种蔬菜包的销售总额为4016元,其中、两种蔬菜包的销售利润共826元.第二天生鲜超市准备的、、三种蔬菜包的数量和第一天完全相同,而蔬菜包的成本增加了,售价不变,蔬菜包的成本不变,利润率变为,蔬菜包的成本和售价均保持不变,但在运送过程中蔬菜包的损坏无法销售,则第二天三种蔬菜包销售完后的总利润为 962 元.
【答案】962.
【分析】分别计算出、、三种蔬菜包第一天的售价与成本,根据已知的第一天的销售总额和利润,列方程组计算出三种蔬菜包第一天的销售量,在此基础上计算第二天的总成本与销售总额,进而求得总利润.
【解答】解:蔬菜包的成本为元,售价为32元,
蔬菜包的成本为36元,售价为元,
蔬菜包的成本为元,售价为60元,
设第一天超市准备的、、三种蔬菜包的数量分别为,,,
则,且,,均为整数,
解得,
因此根据题意,第二天蔬菜包的成本为每包元,售价每包32元,
蔬菜包的成本为每包36元,售价为(元,
蔬菜包的成本为每包为42元,进货数量为35包,售价为每包60元,销售数量为(包,
第二天的总销售额为:(元,
总成本为:(元,
总利润为:(元,
故答案为:962.
50.(2021秋 绵阳期末)有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:
总积分
9
7
(1)某球队要取得一场比赛的胜利,可能的比分结果是什么?
(2)若比分为时,净胜球为2,比分为时,净胜球为1,依此类推,净胜球越多,积分也越多.请你根据表格中的数据,求出各种比分对应的积分分别是什么?
(3)在(2)的条件下,若球队战胜了球队,但总积分,求,的值.
【答案】(1)或;
(2)比分为,,,时,每场的积分分别为4,3,2,1;
(3),.
【分析】(1)根据比赛情况可得可能的比分为和;
(2)设比分为,,,每场的积分分别为,,,,根据表中队、队的积分得,,解方程组再结合且整数,可得答案;
(3)根据球队战胜了球队,分四种情况可得答案.
【解答】解:(1)某球队要取得一场比赛的胜利,可能的比分结果是或;
(2)设比分为,,,每场的积分分别为,,,,
这里的,,,都是整数,且,
根据表中队、队的积分得,,
①②,得,
,且整数,
,
而此时若,不妨假设,则为满足只能为5,
那么,与矛盾,且当时,无法同时满足和,
,
,
,
,
,,
,
,
,
,,,,
答:比分为,,,时,每场的积分分别为4,3,2,1;
(3)若是,则是,
,
,
符合队战胜队,不符合,
若是,则是,
,,符合队战胜队,符合,
若是,则是,
,,不符合队战胜队,符合,
若是,则是,
,,不符合队战胜队,符合.
综上,符合队战胜队,又符合的,值是,.
培优突破练习【10个考点50题专练】
2023 2024学年华东师大版数学七年级下册
一.二元一次方程的解(共4小题)
1.(2023秋 紫金县期末)已知和是二元一次方程的两个解,则,的值分别为
A.2, B.,1 C.,2 D.1,
2.(2023 南岗区校级开学)已知是方程的一个解,那么的值为
A. B.2 C.3 D.6
3.(2023 西山区校级开学)二元一次方程的正整数解有
A.1组 B.2组 C.3组 D.4组
4.(2023春 霸州市期末)已知关于,的二元一次方程●中的系数让墨迹盖住了,但是知道它一组解是,那么●的值是
A.2 B.1 C. D.
二.解二元一次方程(共2小题)
5.(2023秋 三元区期末)把方程变形,用含的代数式表示,则 .
6.(2023秋 东港区期中)如果把方程写成用含的代数式表示的形式,那么 .
三.由实际问题抽象出二元一次方程(共1小题)
7.(2023秋 高碑店市期末)某校为了培养学生阅读的习惯,准备把一批课外书分给学生阅读,一共有名学生,本课外书,若每名学生发3本,则少3本课外书;若每名学生发2本,则多9本课外书.有下列4个方程:①;②;③;④.其中符合题意的是
A.②③ B.①③ C.②④ D.①④
四.二元一次方程的应用(共3小题)
8.(2022秋 城口县校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大45,这样的两位数共有
A.2个 B.3个 C.4个 D.5个
9.(2023秋 城关区校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 个.
10.(2023秋 西城区期末)“幻方”最早记载于春秋时期的《大戴礼》中,现将1,2,3,4,5,7,8,9这八个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.若按同样的要求重新填数如图2所示,则的值是 ,的值是 .
五.二元一次方程组的定义(共1小题)
11.(2023秋 抚州期中)下列方程组中,是二元一次方程组的是
A. B.
C. D.
六.二元一次方程组的解(共9小题)
12.(2021春 萧山区期中)已知关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为
A. B. C. D.
13.(2023春 内江期末)关于、的二元一次方程组的解是二元一次方程的一个解,则的值是
A. B. C.2 D.4
14.(2022秋 青羊区校级期末)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为 .
15.(2023春 吴兴区校级期末)关于,的二元一次方程组的解满足,则的值是 .
16.(2022春 合浦县期中)方程组的解满足是常数),
(1)求的值.
(2)直接写出关于,的方程的正整数解
17.(2021春 沙依巴克区校级期中)已知关于,的方程组.
(1)请写出方程的所有正整数的解;
(2)若方程组的解满足,求的值.
(3)无论实数取何值,方程总有一个公共解,你能求出这个公共解吗?
(4)如果方程组有整数解,求整数的值.
18.(2021春 江阴市校级月考)已知关于,的方程组与的解相同,求,的值.
19.(2023春 沈丘县月考)已知关于,的方程组,
(1)若方程组的解满足方程,求的值;
(2)请你给出的一个值,使方程组的解中,都是正整数,并直接写出方程组的解.
20.(2021春 松桃县期末)解关于的方程组时,甲正确解出,乙因把抄错了,误解为,求、、的值.
七.解二元一次方程组(共4小题)
21.(2012春 华容县期末)已知,则的值为
A . B . C . 1 D .
22.(2022秋 文山市期末)方程组的解是
A. B. C. D.
23.(2022秋 冷水滩区期中)对于实数,规定新运算:,其中、是常数.已知,.
(1)求、的值;
(2)求的值.
24.(2022春 仁化县期中)已知关于,的二元一次方程的解有和.
(1)求,的值.
(2)当时,的值.
(3)当为何值时,?
八.由实际问题抽象出二元一次方程组(共5小题)
25.(2023秋 萧县期末)《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问:几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问:多久后甲、乙相逢?设甲出发日,乙出发日后甲、乙相逢,则所列方程组正确的是
A. B.
C. D.
26.(2023 南山区校级三模)某校劳动课学习制作娃娃和沙包,已知每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物.布料没有剩余,礼物也恰好成套.设做娃娃用了米布,做沙包用了米布,则
A. B.
C. D.
27.(2022秋 祥符区期末)端午节前夕,某超市用1680元购进、两种商品共60件,其中型商品每件24元,型商品每件36元.设购买型商品件、型商品件,依题意列方程组正确的是
A. B.
C. D.
28.(2023 定海区模拟)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是
A. B.
C. D.
29.(2023 二道区校级模拟)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为 .
九.二元一次方程组的应用(共16小题)
30.(2023秋 香坊区校级期中)某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,问应该分配 名工人生产螺栓,才能使当天的螺栓和螺母刚好配套?
A.13 B.14 C.15 D.16
31.(2022秋 翁源县期末)2022年卡塔尔世界杯欧洲区预选赛中,某国家队参加了10场比赛,仅负1场,共积23分,按比赛规则,胜一场得3分,平一场得1分,负一场得0分,则该队共胜了 场
A.4 B.5 C.6 D.7
32.(2023 蕉岭县一模)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出十一,盈八;人出九,不足十二.问物价几何?译文为:现有一些人共同买一个物品,每人出11元,还盈余8元;每人出9元,则还差12元.问这个物品的价格是多少元?
A.118 B.102 C.88 D.78
33.(2023春 霸州市期末)有这样一道数学题:只闻隔壁人分银,不知多少银和人,每人半斤多半斤,每人九两少一两,试问各位善算者,多少人分多少银?其大意为有一群人分若干两银子,如果每人分半斤,则剩半斤,如果每人分9两,则少1两,问多少人分多少两银子?(注这里的斤是指市斤,1市斤两)
A.9人,64两 B.9人,80两 C.10人,89两 D.10人,85两
34.(2023 碑林区校级开学)《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五:人出八,不足三.问人数几何?”题意是:若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.则买羊的人有 个.
35.(2023秋 沈河区期末)在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为 .
36.(2022秋 太原期末)兔年春节之际,小文和几个同学要用自己的压岁钱为社区敬老院购买春节礼品,如果每人出80元,那么可剩余36元;如果每人出70元,那么还差14元.参加此次活动的共有 人.
37.(2023秋 松江区期末)如图,在大长方形中,放入8个一样形状和大小的小长方形,则图中阴影部分面积为 平方厘米.
38.(2023 栾城区校级开学)用白铁皮制作罐头盒,每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮,用 张制作盒身, 张制作盒底,能使盒身和盒底恰好配套.
39.(2022春 忠县校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某公司有31吨货物,计划同时租用型车辆,型车辆,一次运完,且每辆车都装满货物.根据以上信息解答下列问题:
(1)一辆型车和一辆型车装满货物一次各运多少吨?
(2)请你帮公司设计租车方案.
(3)若型车每辆租金100元,型车每辆租金120元,哪种方案租金最少?
40.(2021秋 驻马店期末)医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
41.(2022春 霍林郭勒市校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某物流公司现有36吨货物,计划同时租用型车辆,型车辆,(要求既有型车又有型车)一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆型车和1辆型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
42.(2022春 海丰县期末)温州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 套(含39套) 套(含79套) 80套及以上
每套服装的价格 80元 70元 60元
经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,两个乐团共需花费5600元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调人,从乙乐团抽调人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
43.(2023秋 萧县期末)两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数,已知前一个四位数比后一个四位数大2178,求这两个两位数.
44.(2021 安徽模拟)甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价,乙商品提价,调价后,两种商品的单价和比原来的单价和提高了.问甲、乙两种商品原来的单价各是多少元?
45.(2023春 江源区期末)如图,宽为长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少?
一十.三元一次方程组的应用(共5小题)
46.(2023 武汉模拟)在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为,其内部的格点数记为,边界上的格点数记为,例如,图中的是格点三角形,其中,,;图中格点多边形所对应的,,分别是,,.经探究发现,任意格点多边形的面积可表示为,其中,,为常数,则当,时,的值为
A.44 B.43 C.100 D.99
47.(2023 沙坪坝区校级开学)传统文化中,橙子和柿子都是带有美好寓意的水果.今年春节,津南果品店就推出了由奉节脐橙和城口磨盘柿组成的甲、乙、丙、丁四种礼盒,其中甲礼盒有1千克脐橙,乙礼盒有1千克磨盘柿,丙礼盒有2千克脐橙和1千克磨盘柿.丁礼盒有以1千克脐橙和2千克磨盘柿.每种礼盒的售价为所含果品的售价之和,两种果品每千克的售价均为整数(磨盘柿比脐橙贵),且每千克的售价之和介于30元与40元之间.第一天试销,甲、乙、丙、丁四种礼盒的销售数量之比为.第二天果品店将甲礼盒改为2千克脐橙,乙礼盒改为2千克磨盘柿.丙礼盒改为9千克脐橙和6千克磨盘柿.丁礼盒改为6千克脐橙和8千克磨盘柿.当天甲、丙、丁这三种含有脐橙的礼盒销售数量之比为.且这三种礼盒的销售总额比第一天四种礼盒的销售总额少6410元.而乙礼盒销售数量则为第一天的,从果品种类统计发现,这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,则这两天甲礼盒的总销售额为 .
48.(2023春 温州月考)购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
49.(2023春 渝中区校级月考)为方便居家期间生活,生鲜超市为某小区业主准备了、、三种类型的蔬菜包销售(整包销售).第一天销售时,蔬菜包的售价为每包32元,利润率为,蔬菜包成本为每包36元,每包提价14元销售,蔬菜包每包的成本是蔬菜包每包成本的,售价为每包60元,且蔬菜包的销售数量不少于20包,第一天将所有准备的蔬菜包全部销售完后,三种蔬菜包的销售总额为4016元,其中、两种蔬菜包的销售利润共826元.第二天生鲜超市准备的、、三种蔬菜包的数量和第一天完全相同,而蔬菜包的成本增加了,售价不变,蔬菜包的成本不变,利润率变为,蔬菜包的成本和售价均保持不变,但在运送过程中蔬菜包的损坏无法销售,则第二天三种蔬菜包销售完后的总利润为 元.
50.(2021秋 绵阳期末)有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:
总积分
9
7
(1)某球队要取得一场比赛的胜利,可能的比分结果是什么?
(2)若比分为时,净胜球为2,比分为时,净胜球为1,依此类推,净胜球越多,积分也越多.请你根据表格中的数据,求出各种比分对应的积分分别是什么?
(3)在(2)的条件下,若球队战胜了球队,但总积分,求,的值.
答案解析
一.二元一次方程的解(共4小题)
1.(2023秋 紫金县期末)已知和是二元一次方程的两个解,则,的值分别为
A.2, B.,1 C.,2 D.1,
【答案】
【分析】把方程组的解代入方程组,得出关于、的方程组,解方程组即可.
【解答】解:和是二元一次方程的两个解,
,
①②,得,,
,
故选:.
2.(2023 南岗区校级开学)已知是方程的一个解,那么的值为
A. B.2 C.3 D.6
【答案】
【分析】把,代入方程得出方程,求的值即可.
【解答】解:,是方程的一个解,
,
解得:,
故选:.
3.(2023 西山区校级开学)二元一次方程的正整数解有
A.1组 B.2组 C.3组 D.4组
【答案】
【分析】用含的式子表示出,求出所有的正整数解即可得出答案.
【解答】解:由得:,
当时,;
当时,;
当时,;
二元一次方程的正整数解有3组,
故选:.
4.(2023春 霸州市期末)已知关于,的二元一次方程●中的系数让墨迹盖住了,但是知道它一组解是,那么●的值是
A.2 B.1 C. D.
【答案】
【分析】根据方程解的意义列方程求解.
【解答】解:设,
由题意得:,
解得:,
故选:.
二.解二元一次方程(共2小题)
5.(2023秋 三元区期末)把方程变形,用含的代数式表示,则 .
【答案】.
【分析】移项即可.
【解答】解:移项得,,
故答案为:.
6.(2023秋 东港区期中)如果把方程写成用含的代数式表示的形式,那么 .
【答案】.
【分析】将方程移项即可.
【解答】解:由可得:.
故答案为:.
三.由实际问题抽象出二元一次方程(共1小题)
7.(2023秋 高碑店市期末)某校为了培养学生阅读的习惯,准备把一批课外书分给学生阅读,一共有名学生,本课外书,若每名学生发3本,则少3本课外书;若每名学生发2本,则多9本课外书.有下列4个方程:①;②;③;④.其中符合题意的是
A.②③ B.①③ C.②④ D.①④
【答案】
【分析】分别根据书的总量相等和学生的人数相等列出方程即可.
【解答】解:根据书的数量相等可列方程为,根据学生的人数相等可列方程为,
所以符合题意的是①④.
故选:.
四.二元一次方程的应用(共3小题)
8.(2022秋 城口县校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大45,这样的两位数共有
A.2个 B.3个 C.4个 D.5个
【答案】
【分析】设原两位数的十位数字为,且为整数),个位数字为,且为整数),则原两位数可表示为,新两位数可表示为,根据题意得出,整理得,再进一步求解即可.
【解答】解:设原两位数的十位数字为,且为整数),个位数字为,且为整数),
则原两位数可表示为,新两位数可表示为,
根据题意,得:,
整理,得:,
当时,,此时两位数为49,
当时,,此时两位数为38,
当时,,此时两位数为27,
当时,,此时两位数为16,
故选:.
9.(2023秋 城关区校级期末)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 7 个.
【答案】7.
【分析】先设原来的两位数为,根据交换其个位数与十位数的位置,所得新两位数比原两位数大18,列出方程,得出,因此可取1到8个数,并且这8个数的特点都是个位数字比十位数字大2的两位数.
【解答】解:设原来的两位数为,
根据题意可得:
,
解得:,
可取从3到9的所有自然数,
即3、4、5、6、7、8、9,
这样的两位数共有7个,
它们分别是13,24,35,46,57,68,79.
故答案为:7.
10.(2023秋 西城区期末)“幻方”最早记载于春秋时期的《大戴礼》中,现将1,2,3,4,5,7,8,9这八个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.若按同样的要求重新填数如图2所示,则的值是 ,的值是 .
【答案】,3.
【分析】根据每个三角形的三个顶点上的数字之和相等,得,,即可得出结论.
【解答】解:根据题意得:,,
,,
故答案为:,3.
五.二元一次方程组的定义(共1小题)
11.(2023秋 抚州期中)下列方程组中,是二元一次方程组的是
A. B.
C. D.
【答案】
【分析】利用二元一次方程组的定义逐一分析各选项中的方程,即可得出结论.
【解答】解:.方程组含有三个未知数,
方程组不是二元一次方程组,选项不符合题意;
.方程组中方程是二次方程,
方程组不是二元一次方程组,选项不符合题意;
.方程组是二元一次方程组,选项符合题意;
.方程组中方程不是整式方程,
方程组不是二元一次方程组,选项不符合题意.
故选:.
六.二元一次方程组的解(共9小题)
12.(2021春 萧山区期中)已知关于,的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为
A. B. C. D.
【答案】
【分析】根据题意①②得,然后根据题意列出方程组即可求得公共解.
【解答】解:①②得,
根据题意,这些方程有一个公共解,与的取值无关,
解得
所以这个公共解为
故选:.
13.(2023春 内江期末)关于、的二元一次方程组的解是二元一次方程的一个解,则的值是
A. B. C.2 D.4
【答案】
【分析】先利用加减消元法解方程组得到方程组的解为,再把代入方程中求出的值即可.
【解答】解:
①②得:,解得,
把代入①得:,解得,
方程组的解为,
关于、的二元一次方程组的解是二元一次方程的一个解,
,
,
故选:.
14.(2022秋 青羊区校级期末)若关于,的二元一次方程组的解也是二元一次方程的解,则的值为 4 .
【答案】4.
【分析】求方程组的解,将它代入方程,求出的值即可.
【解答】解:解方程组,得,
将代入方程,得,解得.
故答案为:4.
15.(2023春 吴兴区校级期末)关于,的二元一次方程组的解满足,则的值是 .
【答案】.
【分析】将两式相加,得到,然后得到,据此即可求解.
【解答】解:,
由②①得,
,
,
,
解得.
故答案为:.
16.(2022春 合浦县期中)方程组的解满足是常数),
(1)求的值.
(2)直接写出关于,的方程的正整数解
【分析】(1)先求出方程组的解,再代入方程,即可求出值;
(2)把的值代入方程,再求出正整数解即可.
【解答】解:(1)方程组的解为:,
将代入得:,
解得:;
(2)把代入方程得:,
即,
所以关于,的方程的正整数解为,.
17.(2021春 沙依巴克区校级期中)已知关于,的方程组.
(1)请写出方程的所有正整数的解;
(2)若方程组的解满足,求的值.
(3)无论实数取何值,方程总有一个公共解,你能求出这个公共解吗?
(4)如果方程组有整数解,求整数的值.
【答案】(1),;
(2);
(3);
(4)或2.
【分析】(1)把看作已知数表示出,进而确定出方程的正整数解即可;
(2)已知方程与方程组第一个方程联立求出与的值,进而求出的值;
(3)方程变形后,确定出公共解即可;
(4)根据方程组有整数解,确定出整数的值即可.
【解答】解:(1)方程,
解得:,
当时,;,;
即方程的正整数的解为,;
(2)联立得,
解得,
代入得:,
解得;
(3),即总有一个解,
方程的解与无关,
,,
解得:,,
则方程的公共解为;
(4),
①②得:,
解得:,
把代入①得:,
当,1,,,4,时,为整数,此时.,,,2,,
当时,,不符合题意;
当时,,不符合题意;
当时,,符合题意;
当时,,符合题意,
当时,,不符合题意;
当时,,不符合题意,
综上所述,整数的值为或2.
18.(2021春 江阴市校级月考)已知关于,的方程组与的解相同,求,的值.
【分析】联立两个方程组中不含与的方程组成方程组,求出解确定出与的值即可.
【解答】解:联立得:,
①②得:,即,
把代入①得:,
把,代入得:,
解得:,.
19.(2023春 沈丘县月考)已知关于,的方程组,
(1)若方程组的解满足方程,求的值;
(2)请你给出的一个值,使方程组的解中,都是正整数,并直接写出方程组的解.
【分析】(1)由方程组解出、,再代入即可解决问题.
(2)是大于3的整数,任意取一个值即可.
【解答】解:(1)由,解得
把,代入,得
.
(2),则,.(答案不唯一).
20.(2021春 松桃县期末)解关于的方程组时,甲正确解出,乙因把抄错了,误解为,求、、的值.
【分析】把甲的解代入方程组,乙因把抄错了,方程组中第一个方程不含,把乙的解代入方程组中第一个方程,列三元一次方程组求、、的值.
【解答】解:依题意,得,
③①得,解得,
把代入③,得,
由②得,
所以,,,.
七.解二元一次方程组(共4小题)
21.(2012春 华容县期末)已知,则的值为
A . B . C . 1 D .
【分析】利用非负数的性质列出关于与的方程组, 求出方程组的解得到与的值, 即可求出所求式子的值 .
【解答】解:,
,
①②得:,即,
将代入①得:,即,
则原式.
故选:.
22.(2022秋 文山市期末)方程组的解是
A. B. C. D.
【答案】
【分析】根据代入消元法求解.
【解答】解:由第二个方程得:③,
把③代入第一个方程得:,
解得:,
把代入③得:,
故选:.
23.(2022秋 冷水滩区期中)对于实数,规定新运算:,其中、是常数.已知,.
(1)求、的值;
(2)求的值.
【分析】(1)利用新定义和两组对应值得到,然后利用加减法解方程组即可;
(2)由(1)得新运算为:,然后把,代入计算即可.
【解答】解:(1)根据题意得,
解得,;
(2)由(1)得,
所以.
24.(2022春 仁化县期中)已知关于,的二元一次方程的解有和.
(1)求,的值.
(2)当时,的值.
(3)当为何值时,?
【分析】(1)将两组,的值代入方程得出关于、的二元一次方程组,再运用加减消元法求出、的值.
(2)将(1)中的、代入,再把代入化简即可得出的值.
(3)将(1)中的、和代入方程化简即可得出的值.
【解答】解:
(1)依题意得:
①②得:,
所以,
所以.
(2)由,
把代入,得.
(3)由
把代入,得.
八.由实际问题抽象出二元一次方程组(共5小题)
25.(2023秋 萧县期末)《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问:几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问:多久后甲、乙相逢?设甲出发日,乙出发日后甲、乙相逢,则所列方程组正确的是
A. B.
C. D.
【答案】
【分析】可将此题看作是工作效率类的应用题,根据效率时间总量列方程即可.
【解答】解:由题可知,甲的效率为,乙的效率为,
设甲出发日,乙出发日后甲、乙相逢,根据题意列方程组:
.
故选:.
26.(2023 南山区校级三模)某校劳动课学习制作娃娃和沙包,已知每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物.布料没有剩余,礼物也恰好成套.设做娃娃用了米布,做沙包用了米布,则
A. B.
C. D.
【答案】
【分析】根据“每米布可做娃娃25个或沙包40个.现有36米布料,完成后打算将1个娃娃和2个沙包配成一套礼物”,即可得出关于,的二元一次方程组,此题得解.
【解答】解:依题意得:.
故选:.
27.(2022秋 祥符区期末)端午节前夕,某超市用1680元购进、两种商品共60件,其中型商品每件24元,型商品每件36元.设购买型商品件、型商品件,依题意列方程组正确的是
A. B.
C. D.
【答案】
【分析】根据题意,由超市用1680元购进,两种商品,结合两种商品的单价可得到一个方程;再由,两种商品共60件得到另一个方程,联立即可得到答案.
【解答】解:由题意得:,
,
.
故选:.
28.(2023 定海区模拟)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有个人,该物品价格是元,则下列方程组正确的是
A. B.
C. D.
【答案】
【分析】根据“人数物品价值、物品价值人数”可得方程组.
【解答】解:若设有人,物品价值元,根据题意,可列方程组为,
故选:.
29.(2023 二道区校级模拟)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,那么可列方程组为 .
【分析】设大马有匹,小马有匹,由题意得等量关系:①共有马100匹;②大马拉瓦数小马拉瓦数,根据等量关系,列出方程组即可.
【解答】解:设大马有匹,小马有匹,由题意得:
,
故答案为:.
九.二元一次方程组的应用(共16小题)
30.(2023秋 香坊区校级期中)某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,问应该分配 名工人生产螺栓,才能使当天的螺栓和螺母刚好配套?
A.13 B.14 C.15 D.16
【答案】
【分析】设应该分配名工人生产螺栓,人生产螺母,才能使当天的螺栓和螺母刚好配套,根据某车间35名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个.一个螺栓要配两个螺母,列出二元一次方程组,解方程组即可.
【解答】解:设应该分配名工人生产螺栓,人生产螺母,才能使当天的螺栓和螺母刚好配套,
由题意得:,
解得:,
即应该分配15名工人生产螺栓,20人生产螺母,才能使当天的螺栓和螺母刚好配套,
故选:.
31.(2022秋 翁源县期末)2022年卡塔尔世界杯欧洲区预选赛中,某国家队参加了10场比赛,仅负1场,共积23分,按比赛规则,胜一场得3分,平一场得1分,负一场得0分,则该队共胜了 场
A.4 B.5 C.6 D.7
【答案】
【分析】设该队共胜场,则平场,由题意知,,计算求解即可.
【解答】解:设该队共胜场,则平场,
由题意知,,
解得,
该队共胜7场,
故选:.
32.(2023 蕉岭县一模)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出十一,盈八;人出九,不足十二.问物价几何?译文为:现有一些人共同买一个物品,每人出11元,还盈余8元;每人出9元,则还差12元.问这个物品的价格是多少元?
A.118 B.102 C.88 D.78
【答案】
【分析】设共有人,这个物品的价格是元,根据每人出11元,还盈余8元;每人出9元,则还差12元.列出二元一次方程组,解方程组即可.
【解答】解:设共有人,这个物品的价格是元,
由题意得:,
解得:,
即这个物品的价格是102元,
故选:.
33.(2023春 霸州市期末)有这样一道数学题:只闻隔壁人分银,不知多少银和人,每人半斤多半斤,每人九两少一两,试问各位善算者,多少人分多少银?其大意为有一群人分若干两银子,如果每人分半斤,则剩半斤,如果每人分9两,则少1两,问多少人分多少两银子?(注这里的斤是指市斤,1市斤两)
A.9人,64两 B.9人,80两 C.10人,89两 D.10人,85两
【答案】
【分析】设有个人,共分两银子,根据如果每人分半斤,则剩半斤,如果每人分9两,则少1两,列出二元一次方程组,解方程组即可.
【解答】解:设有个人,共分两银子,
根据题意得:,
解得:,
即有9个人,共分80两银子,
故选:.
34.(2023 碑林区校级开学)《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五:人出八,不足三.问人数几何?”题意是:若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.则买羊的人有 21 个.
【答案】21.
【分析】设买羊的人有个,羊价为元,根据若干人共同出资买羊,每人出6元,则差45元;每人出8元,则差3元.列出二元一次方程组,解方程组即可.
【解答】解:设买羊的人有个,羊价为元,
由题意得:,
解得:,
即买羊的人有21个,
故答案为:21.
35.(2023秋 沈河区期末)在长方形中,放入5个形状大小相同的小长方形(空白部分),其中,,则阴影部分图形的总面积为 27 .
【答案】27.
【分析】设小长方形的长为 ,宽为 ,根据图形中大长方形的长和宽列二元一次方程组,解方程组,即可解决问题.
【解答】解:设小长方形的长为 ,宽为 ,
根据题意得:,
解得:,
,
即每个小长方形的面积为,
阴影部分的面积,
故答案为:27.
36.(2022秋 太原期末)兔年春节之际,小文和几个同学要用自己的压岁钱为社区敬老院购买春节礼品,如果每人出80元,那么可剩余36元;如果每人出70元,那么还差14元.参加此次活动的共有 5 人.
【答案】5.
【分析】设此次参加活动的共有人,根据购买春节礼品的总钱数不变,可得方程,解之即可.
【解答】解:设此次参加活动的共有人,
由题意可得:,
解得:,
此次参加活动的共有5人,
故答案为:5.
37.(2023秋 松江区期末)如图,在大长方形中,放入8个一样形状和大小的小长方形,则图中阴影部分面积为 92 平方厘米.
【答案】92.
【分析】根据图中的数据,可以列出相应的二元一次方程组,然后即可求得小长方形的长和宽,然后即可计算出图中阴影部分的面积.
【解答】解:设小长方形的长为 ,宽为 ,
由图可得:,
解得,
图中阴影部分的面积为:
(平方厘米),
故答案为:92.
38.(2023 栾城区校级开学)用白铁皮制作罐头盒,每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮,用 20 张制作盒身, 张制作盒底,能使盒身和盒底恰好配套.
【答案】20,16.
【分析】设用张制作盒身,张制作盒底,由“每张铁皮可制作盒身16个或者盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮”,列出二元一次方程组,解方程组即可.
【解答】解:设用张制作盒身,张制作盒底,
由题意得:,
解得:,
用20张制作盒身,16张制作盒底,
故答案为:20,16.
39.(2022春 忠县校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某公司有31吨货物,计划同时租用型车辆,型车辆,一次运完,且每辆车都装满货物.根据以上信息解答下列问题:
(1)一辆型车和一辆型车装满货物一次各运多少吨?
(2)请你帮公司设计租车方案.
(3)若型车每辆租金100元,型车每辆租金120元,哪种方案租金最少?
【答案】(1)1辆型车装满货物一次可运货3吨,1辆型车装满货物一次可运货4吨;
(2)该物流公司共有3种租车方案,
方案1:租用型车1辆,型车7辆;
方案2:租用型车5辆,型车4辆;
方案3:租用型车9辆,型车1辆;
(3)方案1:租用型车1辆,型车7辆最省钱,最少租车费为940元.
【分析】(1)设1辆型车装满货物一次可运货吨,1辆型车装满货物一次可运货吨,根据“用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨”,即可得出关于,的二元一次方程组,解之即可得出结论;
(2)设租用辆型车,辆型车,根据租用的两种型号车满载货物一次可运货31吨,即可得出关于,的二元一次方程,结合,均为正整数,即可得出各租车方案;
(3)利用总租金每辆车的租金租用该车型数量,可分别求出各租车方案所需租车费,比较后即可得出结论.
【解答】解:(1)设1辆型车装满货物一次可运货吨,1辆型车装满货物一次可运货吨,
依题意得:,
解得:.
答:1辆型车装满货物一次可运货3吨,1辆型车装满货物一次可运货4吨.
(2)设租用辆型车,辆型车,
依题意得:,
.
又,均为正整数,
或或,
该物流公司共有3种租车方案,
方案1:租用型车1辆,型车7辆;
方案2:租用型车5辆,型车4辆;
方案3:租用型车9辆,型车1辆.
(3)租车方案1所需费用(元;
租车方案2所需费用(元;
租车方案3所需费用(元.
,
方案1:租用型车1辆,型车7辆最省钱,最少租车费为940元.
40.(2021秋 驻马店期末)医院用甲、乙两种原料为手术后的病人配制营养品,每克甲种原料含0.5单位的蛋白质和1单位铁质,每克乙种原料含0.7单位的蛋白质和0.4单位铁质.若病人每餐需要35单位的蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰能满足病人的需要?
【分析】本题中可将等量关系列为每餐中甲含的蛋白质的量乙含的蛋白质的量,每餐中甲含的铁质的量乙含的铁质的量.由此列出方程组求解.
【解答】解:设每餐需甲原料克,乙原料克,
根据题意可列方程组
解得:.
答:每餐需甲种原料28克,乙种原料30克.
41.(2022春 霍林郭勒市校级期中)已知:用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨.某物流公司现有36吨货物,计划同时租用型车辆,型车辆,(要求既有型车又有型车)一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆型车和1辆型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
【答案】(1)1辆型车和1辆型车都装满货物一次可分别运货3吨,4吨;
(2)故共有两种租车方案,分别为:①型车4辆,型车6辆;②型车8辆,型车3辆.
【分析】(1)设1辆型车和1辆型车都装满货物一次可分别运货吨,吨,根据“用2辆型车和1辆型车装满货物一次可运货10吨;用1辆型车和2辆型车装满货物一次可运货11吨”,即可得出关于、的二元一次方程组,解之即可得出结论;
(2)由(1)的结论结合某物流公司现有31吨货物,即可得出,即,由、均为正数即可得出各租车方案.
【解答】解:(1)设1辆型车和1辆型车都装满货物一次可分别运货吨,吨,
根据题意得:,
解得:.
答:1辆型车和1辆型车都装满货物一次可分别运货3吨,4吨.
(2)由题意可得:,
.
,均为整数,(要求既有型车又有型车)
有和两种情况.
故共有两种租车方案,分别为:
①型车4辆,型车6辆;
②型车8辆,型车3辆.
42.(2022春 海丰县期末)温州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 套(含39套) 套(含79套) 80套及以上
每套服装的价格 80元 70元 60元
经调查:两个乐团共75人(甲乐团人数不少于40人),如果分别各自购买演出服,两个乐团共需花费5600元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调人,从乙乐团抽调人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
【分析】(1)若甲、乙两个乐团合起来购买服装80套,则每套是60元,计算出总价,即可求得比各自购买服装共可以节省多少钱;
(2)设甲、乙个乐团各有名、名学生准备参加演出.根据题意,显然各自购买时,甲乐团每套服装是70元,乙乐团每套服装是80元.根据等量关系:①共75人;②分别单独购买服装,一共应付5600元,列方程组即可求解;
(3)利用甲乐团每位成员负责3位小朋友,乙乐团每位成员负责5位小朋友恰好使得福利院65位小朋友全部得到“心连心活动”的温暖列出方程探讨答案即可.
【解答】解:(1)买80套所花费为:(元,
最多可以节省:(元.
(2)解:设甲乐团有人;乙乐团有人.
根据题意,得
解得
答:甲乐团有40人;乙乐团有35人.
(3)由题意,得
变形,得
因为每位乐团的人数不少于5人且人数为正整数
得:或.
所以共有两种方案:从甲乐团抽调5人,从乙乐团抽调10人;或者从甲乐团抽调10人,从乙乐团抽调7人.
43.(2023秋 萧县期末)两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数,已知前一个四位数比后一个四位数大2178,求这两个两位数.
【分析】首先设较大的两位数为,较小的两位数为,根据题意可得等量关系:①两个两位数的和为68,②比大2178,根据等量关系列出方程组,再解方程组即可.
【解答】解:设较大的两位数为,较小的两位数为,
根据题意,得
,
化简得:,
即,
解得.
答:这两个数是45和23.
44.(2021 安徽模拟)甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价,乙商品提价,调价后,两种商品的单价和比原来的单价和提高了.问甲、乙两种商品原来的单价各是多少元?
【分析】如果设甲商品原来的单价是元,乙商品原来的单价是元,那么根据“甲、乙两种商品原来的单价和为100元”可得出方程为根据“甲商品降价,乙商品提价,调价后,两种商品的单价之和比原来的单价之和提高了”,可得出方程为.
【解答】解:设甲种商品原来的单价是元,乙种商品原来的单价是元,依题意得
,
解得:.
答:甲种商品原来的单价是40元,乙种商品原来的单价是60元.
45.(2023春 江源区期末)如图,宽为长方形图案由10个相同的小长方形拼成,求每块小长方形的长和宽分别是多少?
【分析】本题可以通过看图找出两个等量关系:长方形的长宽,长方形的长长宽,据此可以设未知数列方程组求解.
【解答】解:设每块小长方形的长是,宽是,根据题意得
解得
答:长是,宽是.
一十.三元一次方程组的应用(共5小题)
46.(2023 武汉模拟)在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为,其内部的格点数记为,边界上的格点数记为,例如,图中的是格点三角形,其中,,;图中格点多边形所对应的,,分别是,,.经探究发现,任意格点多边形的面积可表示为,其中,,为常数,则当,时,的值为
A.44 B.43 C.100 D.99
【答案】
【分析】根据格点多边形的面积,结合图中的格点、格点多边形、格点四边形的、、数值,列出三元一次方程组,解方程组,求出、、的值,即可解决问题.
【解答】解:由题意得:四边形是格点四边形,,,,
任意格点多边形的面积,
由图中的格点、格点多边形、格点四边形得:
,
解得:,
,
将,代入得:,
故选:.
47.(2023 沙坪坝区校级开学)传统文化中,橙子和柿子都是带有美好寓意的水果.今年春节,津南果品店就推出了由奉节脐橙和城口磨盘柿组成的甲、乙、丙、丁四种礼盒,其中甲礼盒有1千克脐橙,乙礼盒有1千克磨盘柿,丙礼盒有2千克脐橙和1千克磨盘柿.丁礼盒有以1千克脐橙和2千克磨盘柿.每种礼盒的售价为所含果品的售价之和,两种果品每千克的售价均为整数(磨盘柿比脐橙贵),且每千克的售价之和介于30元与40元之间.第一天试销,甲、乙、丙、丁四种礼盒的销售数量之比为.第二天果品店将甲礼盒改为2千克脐橙,乙礼盒改为2千克磨盘柿.丙礼盒改为9千克脐橙和6千克磨盘柿.丁礼盒改为6千克脐橙和8千克磨盘柿.当天甲、丙、丁这三种含有脐橙的礼盒销售数量之比为.且这三种礼盒的销售总额比第一天四种礼盒的销售总额少6410元.而乙礼盒销售数量则为第一天的,从果品种类统计发现,这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,则这两天甲礼盒的总销售额为 85 .
【答案】85.
【分析】设磨盘柿和脐橙的单价分别为、,第一天甲四种礼盒的销售数量为,第二天甲四种礼盒的销售数量为,再依据题意列出方程和不等式,最后计算即可.
【解答】解:设磨盘柿和脐橙的单价分别为、,第一天甲四种礼盒的销售数量为,第二天甲四种礼盒的销售数量为,
第一天甲、乙、丙、丁四种礼盒的销售数量依次为、、、,
第二天甲、丙、丁这三种含有脐橙的礼盒销售数量依次为、、,乙礼盒销售数量为,
第一天销售磨盘柿千克,脐橙千克,
第二天三种礼盒销售磨盘柿千克,脐橙千克,
这三种礼盒的第二天销售总额比第一天四种礼盒的销售总额少6410元,
,
整理得,
磨盘柿比脐橙贵,且每千克的售价之和介于30元与40元之间,
,,
,
是质数,
,,
,
这两天通过礼盒方式售出的脐橙与磨盘柿数量相差在65千克到75千克之间,
,
整理得:,
,
解得,
,,
这两天甲礼盒的总销售额为,
故答案为:85.
48.(2023春 温州月考)购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 7 元.
【答案】7.
【分析】首先假设铅笔的单价是元,作业本的单价是元,中性笔的单价是元.购买铅笔2支,作业本1本,中性笔1支共需元.根据题目说明列出方程组,解方程组求出的值,即为所求结果.
【解答】解:设铅笔的单价是元,作业本的单价是元,中性笔的单价是元.购买铅笔2支,作业本1本,中性笔1支共需元.
则由题意得:
,
由①②得,
于是:,
故答案为:7.
49.(2023春 渝中区校级月考)为方便居家期间生活,生鲜超市为某小区业主准备了、、三种类型的蔬菜包销售(整包销售).第一天销售时,蔬菜包的售价为每包32元,利润率为,蔬菜包成本为每包36元,每包提价14元销售,蔬菜包每包的成本是蔬菜包每包成本的,售价为每包60元,且蔬菜包的销售数量不少于20包,第一天将所有准备的蔬菜包全部销售完后,三种蔬菜包的销售总额为4016元,其中、两种蔬菜包的销售利润共826元.第二天生鲜超市准备的、、三种蔬菜包的数量和第一天完全相同,而蔬菜包的成本增加了,售价不变,蔬菜包的成本不变,利润率变为,蔬菜包的成本和售价均保持不变,但在运送过程中蔬菜包的损坏无法销售,则第二天三种蔬菜包销售完后的总利润为 962 元.
【答案】962.
【分析】分别计算出、、三种蔬菜包第一天的售价与成本,根据已知的第一天的销售总额和利润,列方程组计算出三种蔬菜包第一天的销售量,在此基础上计算第二天的总成本与销售总额,进而求得总利润.
【解答】解:蔬菜包的成本为元,售价为32元,
蔬菜包的成本为36元,售价为元,
蔬菜包的成本为元,售价为60元,
设第一天超市准备的、、三种蔬菜包的数量分别为,,,
则,且,,均为整数,
解得,
因此根据题意,第二天蔬菜包的成本为每包元,售价每包32元,
蔬菜包的成本为每包36元,售价为(元,
蔬菜包的成本为每包为42元,进货数量为35包,售价为每包60元,销售数量为(包,
第二天的总销售额为:(元,
总成本为:(元,
总利润为:(元,
故答案为:962.
50.(2021秋 绵阳期末)有四个球队进行单循环比赛,每两队之间只比赛一场,每场比赛实行三局两胜制,即三局中获胜两局就获胜该场比赛,同时停止本场比赛.例如:表中第二行,比分表示队以战胜队.已知球队在每场比赛中都能获得积分,不同比分的积分不同,且积分为正整数.得到的比赛总积分表如下:
总积分
9
7
(1)某球队要取得一场比赛的胜利,可能的比分结果是什么?
(2)若比分为时,净胜球为2,比分为时,净胜球为1,依此类推,净胜球越多,积分也越多.请你根据表格中的数据,求出各种比分对应的积分分别是什么?
(3)在(2)的条件下,若球队战胜了球队,但总积分,求,的值.
【答案】(1)或;
(2)比分为,,,时,每场的积分分别为4,3,2,1;
(3),.
【分析】(1)根据比赛情况可得可能的比分为和;
(2)设比分为,,,每场的积分分别为,,,,根据表中队、队的积分得,,解方程组再结合且整数,可得答案;
(3)根据球队战胜了球队,分四种情况可得答案.
【解答】解:(1)某球队要取得一场比赛的胜利,可能的比分结果是或;
(2)设比分为,,,每场的积分分别为,,,,
这里的,,,都是整数,且,
根据表中队、队的积分得,,
①②,得,
,且整数,
,
而此时若,不妨假设,则为满足只能为5,
那么,与矛盾,且当时,无法同时满足和,
,
,
,
,
,,
,
,
,
,,,,
答:比分为,,,时,每场的积分分别为4,3,2,1;
(3)若是,则是,
,
,
符合队战胜队,不符合,
若是,则是,
,,符合队战胜队,符合,
若是,则是,
,,不符合队战胜队,符合,
若是,则是,
,,不符合队战胜队,符合.
综上,符合队战胜队,又符合的,值是,.
