新人教版数学七年级上册第四章几何图形初步4.1.2《点、线、面、体》课时练习.doc
文档属性
| 名称 | 新人教版数学七年级上册第四章几何图形初步4.1.2《点、线、面、体》课时练习.doc |  | |
| 格式 | doc | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-06 11:49:17 | ||
图片预览



文档简介
新人教版数学七年级上册4.1.2点、线、面、体课时练习
一、选择题
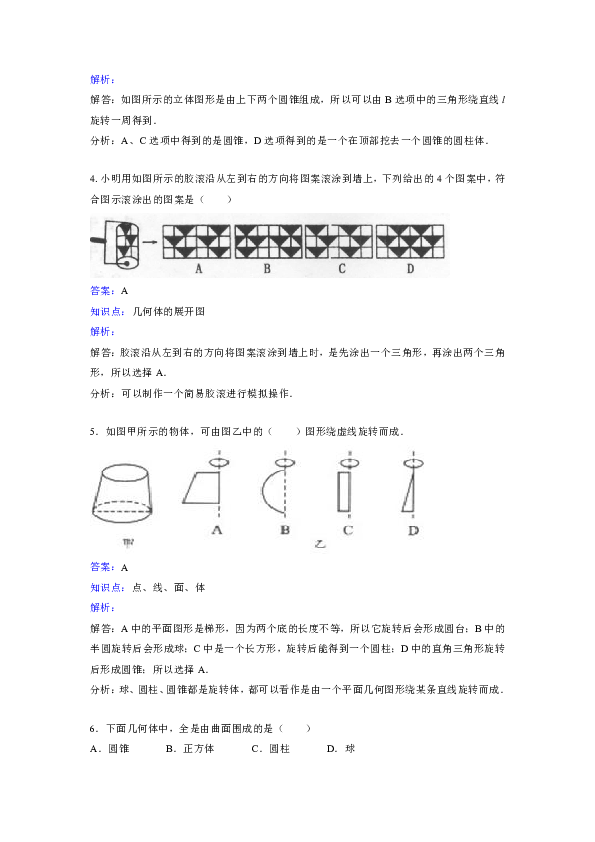
1.如图,下列图形中全部是柱体的有( )
答案:C
知识点:认识立体图形
解析:
解答:A中左下角的图形是三棱锥;B中上面的图形是圆锥,右下角的图形是不规则的多面体;C中的图形是一个圆柱与两个四棱柱;D中上面的图形是圆台.所以选择C.
分析:判断一个立体图形是否为柱体,关键是看该图中是否有两个完全相同且相互平行的面.
2.下列说法正确的个数为( )
(1)柱体的上、下两个面一样大;(2)圆柱的侧面展开图是长方形;(3)正方体有6个顶点;(4)圆锥有2个面,且都是曲面;(5)球仅由1个面围成,这个面是平面;(6)三棱柱有5个面,且都是平面.
A.1 B.2 C.3 D.4
答案:B
知识点:认识立体图形;点、线、面、体
解析:
解答:其中只有(2)与(6)正确,所以选择B.
分析:(1)中,柱体定有两个完全相同且相互平行的面,但两个面的大小不一定一样;(3)中正方体有8个顶点;(4)中圆锥的两个面一个为曲面一个为平面;(5)中围成球的是一个曲面.
3.将三角形绕直线l旋转一周,可以得到如下图所示立体图形的是( )
A B C D
答案:B
知识点:点、线、面、体
解析:
解答:如图所示的立体图形是由上下两个圆锥组成,所以可以由B选项中的三角形绕直线l旋转一周得到.
分析:A、C选项中得到的是圆锥,D选项得到的是一个在顶部挖去一个圆锥的圆柱体.
4.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( )
答案:A
知识点:几何体的展开图
解析:
解答:胶滚沿从左到右的方向将图案滚涂到墙上时,是先涂出一个三角形,再涂出两个三角形,所以选择A.
分析:可以制作一个简易胶滚进行模拟操作.
5.如图甲所示的物体,可由图乙中的( )图形绕虚线旋转而成.
答案:A
知识点:点、线、面、体
解析:
解答:A中的平面图形是梯形,因为两个底的长度不等,所以它旋转后会形成圆台;B中的半圆旋转后会形成球;C中是一个长方形,旋转后能得到一个圆柱;D中的直角三角形旋转后形成圆锥;所以选择A.
分析:球、圆柱、圆锥都是旋转体,都可以看作是由一个平面几何图形绕某条直线旋转而成.
6.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体 C.圆柱 D.球
答案:D
知识点:点、线、面、体;认识立体图形
解析:
解答:A中的圆锥式由一个曲面和一个平面组成;B中的正方体是由平面组成;C中的圆柱是由一个曲面和两个平面组成;D中的球是由一个曲面组成;所以选择D.
分析:圆柱、圆锥、球都含有曲面,棱柱、棱锥全部由平面围成.
7.下列结论,其中正确的为( )
①圆柱由3个面围成,这3个面都是平面.
②圆锥由2个面围成,这2个面中,1个是平的,1个不是平的.
③球仅由1个面围成,这1个面是平的.
④正方体由6个面围成,这6个面都是平的
A.①② B.②③ C.②④ D.③④
答案:C
知识点:点、线、面、体;认识立体图形
解析:
解答:①圆柱由两个平面和一个曲面围成,③球由一个曲面围成,所以只有②④正确.
分析:圆柱、圆锥、球都含有曲面,棱柱、棱锥全部由平面围成.
8.如图所示,下列图形绕着虚线旋转一周得到圆锥体的是( )
答案:D
知识点:点、线、面、体
解析:
解答:A中的平面图形是梯形,因为两个底的长度不等,所以它旋转后会形成圆台;B中的半圆旋转后会形成球;C中是一个长方形,旋转后能得到一个圆柱;D中的直角三角形旋转后形成圆锥;所以选择D.
分析:球、圆柱、圆锥都是旋转体,都可以看作是由一个平面几何图形绕某条直线旋转而成.
9.将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体是图中的( )
答案:D
知识点:点、线、面、体
解析:
解答:将直角三角形绕它的斜边旋转,那么得到的几何体上下应该都有“尖”的部分,所以选择D.
分析:一般的含有曲面的几何体都可以由某一个平面图形旋转得到.
10.如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少需要( )
A.23平方米 B.90平方米 C.130平方米 D.120平方米
答案:B
知识点:几何体的展开图
解析:
解答:地毯的长即楼梯所有台阶的高度与宽度的和即(8+10)米,地毯的宽即台阶的长即5米,所以这块地毯的面积至少为90平方米.
分析:题目中的“至少”是指这块地毯在理想的状况下够用.
11.将如图直角△ABC绕直角边BC旋转一周,所得几何体从它的左面看得到平面图形是( )
A B C D
答案:C
知识点:认识立体图形;点、线、面、体
解析:
解答:如图直角△ABC绕直角边BC旋转一周,所得几何体为“放倒”的圆锥体,所以从它的左面看到的是一个圆形,所以选C.
分析:先根据题目判断得到的几何体的图形,再判断从左面看该几何体的平面图形.
12.汽车的雨刷能把玻璃上的雨水刷干净,这说明( )
A.点动成线 B.线动成面 C.面动成体 D.以上说法都不对
答案:B
知识点:点、线、面、体
解析:
解答:雨刷可以看成一条线,在玻璃上刷出的一片区域为面,所以可以说明线动成面.
分析:理论联系实际,深刻的理解点、线、面、体的概念,给出合理的解释.
13.按组成面的平和曲划分,与圆锥为同一类的几何体是( )
A.棱锥 B.棱柱 C.圆锥 D.长方体
答案:C
知识点:认识立体图形
解析:
解答:圆柱、圆锥都是由曲面和平面组成,棱柱、棱锥全部由平面组成,球全部由曲面组成.
分析:圆柱、圆锥与棱柱、棱锥是不同的两类几何体.
14.想一想:将左边的图形折成一个立方体,那么这个立方体是( )
答案:B
知识点:几何体的展开图
解析:
解答:将左边的图形折成一个正方体时,“梅花”的部分应与画线的部分相对应,所以用排除的方法只能选择B.
分析:可以自制一个简单的图形,将其折叠后也可以选出答案.
15.如图所示,下列图形中不是正方体的展开图是( )
答案:C
知识点:几何体的展开图
解析:
解答:C中折叠后不能成为一个正方体,而是有一个底重合,另一个无底的不完整正方体.
分析:正方体的展开图有11中,是练习同学们空间想象的一个很好的素材.
二、填空题
1.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周形成了一圆锥体,这说明了_____________.
答案:点动成线;线动成面;面动成体
知识点:点、线、面、体
解析:
解答:本题是点、线、面、体间的动态关系在实际生活中理解.
分析:理论联系实际,深刻的理解点、线、面、体的概念,给出合理的解释.
2.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了________个点.
答案:4;6;4
知识点:认识立体图形;点、线、面、体
解析:
解答:三棱锥有4个面,它们相交形成了6条棱, 这些棱相交形成了4个点.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
3.①一段烟囱(无烟囱帽);②一段圆钢;③铅锤;④烟囱帽.①②都呈 的形状;③④都呈 的形状.
答案:圆柱;圆锥
知识点:认识立体图形
解析:
解答:联系生活实际,结合几何体的概念解答本题.
分析:多留心生活中的事物,这类题就很容易解答.
4.如图,观察图形填空;包围着体的是______;面与面相交的地方形成______;线与线相交的地方是_______.
答案:面;线;点
知识点:点、线、面、体
解析:
解答:包围着体的是面,面与面相交的地方形成线,线与线相交的地方是点.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
5.在图中是正方体展开图的有_________.
答案:②④
知识点:几何体的展开图
解析:
解答:①③不能折成正方体.
分析:可以制作题目中所给的展开图,看能否折成正方体.
三、解答题
1.如图,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形
答案:第一个可以得到圆柱;第二个可以得到圆锥;第三个可以得到球
知识点:点、线、面、体
解析:
解答:解:第一个可以得到圆柱;第二个可以得到圆锥;第三个可以得到球.
分析:圆柱可以看作是由长方形某条边所在的直线旋转得到,圆锥可以看作是由直角三角形绕着一条直角边所在直线旋转得到,球可以看作是由圆绕某条直径所在直线旋转得到.
2.如下图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.
答案:如图所示
知识点:点、线、面、体
解析:
解答:解:如图所示:
分析:这些也都是“面动成体”的体现.
3.如图所示,用字母M表示与A相对的面,请在下面的正方体展开图中填写相应的字母.
答案:如图所示
知识点:几何体的展开图
解析:
解答:解:如图所示:
分析:可以通过模型,动手试一试,可以得到答案.
4.(1)如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.
图形 顶点数 边数 区域数
(1) 4 6 3
(2)
(3)
(4)
(2)观察上表,推断一个平面图形的顶点数,边数,区域数之间有什么关系?
答案:(1)如图所示;(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1
知识点:点、线、面、体
解析:
解答:解:(1)通过观察,填表如下:
图形 顶点数 边数 区域数
(1) 4 6 3
(2) 8 12 5
(3) 6 9 4
(4) 10 15 6
(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1.
分析:可以制作题目中所给的展开图,看能否折成正方体关键是确定好每一个图形的顶点数、区域数和边数,这是寻找规律的基础.
5.图中的几何体由几个面围城?面与面相交成几条线?它们中有几条是直的,几条是曲的?
答案:图中几何体由7个面围城;面与面相交成15条线;它们中有15条是直的,0条是曲的.
知识点:点、线、面、体
解析:
解答:解:图中几何体由7个面围城;面与面相交成15条线;它们中有15条是直的,0条是曲的.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
一、选择题
1.如图,下列图形中全部是柱体的有( )
答案:C
知识点:认识立体图形
解析:
解答:A中左下角的图形是三棱锥;B中上面的图形是圆锥,右下角的图形是不规则的多面体;C中的图形是一个圆柱与两个四棱柱;D中上面的图形是圆台.所以选择C.
分析:判断一个立体图形是否为柱体,关键是看该图中是否有两个完全相同且相互平行的面.
2.下列说法正确的个数为( )
(1)柱体的上、下两个面一样大;(2)圆柱的侧面展开图是长方形;(3)正方体有6个顶点;(4)圆锥有2个面,且都是曲面;(5)球仅由1个面围成,这个面是平面;(6)三棱柱有5个面,且都是平面.
A.1 B.2 C.3 D.4
答案:B
知识点:认识立体图形;点、线、面、体
解析:
解答:其中只有(2)与(6)正确,所以选择B.
分析:(1)中,柱体定有两个完全相同且相互平行的面,但两个面的大小不一定一样;(3)中正方体有8个顶点;(4)中圆锥的两个面一个为曲面一个为平面;(5)中围成球的是一个曲面.
3.将三角形绕直线l旋转一周,可以得到如下图所示立体图形的是( )
A B C D
答案:B
知识点:点、线、面、体
解析:
解答:如图所示的立体图形是由上下两个圆锥组成,所以可以由B选项中的三角形绕直线l旋转一周得到.
分析:A、C选项中得到的是圆锥,D选项得到的是一个在顶部挖去一个圆锥的圆柱体.
4.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的4个图案中,符合图示滚涂出的图案是( )
答案:A
知识点:几何体的展开图
解析:
解答:胶滚沿从左到右的方向将图案滚涂到墙上时,是先涂出一个三角形,再涂出两个三角形,所以选择A.
分析:可以制作一个简易胶滚进行模拟操作.
5.如图甲所示的物体,可由图乙中的( )图形绕虚线旋转而成.
答案:A
知识点:点、线、面、体
解析:
解答:A中的平面图形是梯形,因为两个底的长度不等,所以它旋转后会形成圆台;B中的半圆旋转后会形成球;C中是一个长方形,旋转后能得到一个圆柱;D中的直角三角形旋转后形成圆锥;所以选择A.
分析:球、圆柱、圆锥都是旋转体,都可以看作是由一个平面几何图形绕某条直线旋转而成.
6.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体 C.圆柱 D.球
答案:D
知识点:点、线、面、体;认识立体图形
解析:
解答:A中的圆锥式由一个曲面和一个平面组成;B中的正方体是由平面组成;C中的圆柱是由一个曲面和两个平面组成;D中的球是由一个曲面组成;所以选择D.
分析:圆柱、圆锥、球都含有曲面,棱柱、棱锥全部由平面围成.
7.下列结论,其中正确的为( )
①圆柱由3个面围成,这3个面都是平面.
②圆锥由2个面围成,这2个面中,1个是平的,1个不是平的.
③球仅由1个面围成,这1个面是平的.
④正方体由6个面围成,这6个面都是平的
A.①② B.②③ C.②④ D.③④
答案:C
知识点:点、线、面、体;认识立体图形
解析:
解答:①圆柱由两个平面和一个曲面围成,③球由一个曲面围成,所以只有②④正确.
分析:圆柱、圆锥、球都含有曲面,棱柱、棱锥全部由平面围成.
8.如图所示,下列图形绕着虚线旋转一周得到圆锥体的是( )
答案:D
知识点:点、线、面、体
解析:
解答:A中的平面图形是梯形,因为两个底的长度不等,所以它旋转后会形成圆台;B中的半圆旋转后会形成球;C中是一个长方形,旋转后能得到一个圆柱;D中的直角三角形旋转后形成圆锥;所以选择D.
分析:球、圆柱、圆锥都是旋转体,都可以看作是由一个平面几何图形绕某条直线旋转而成.
9.将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体是图中的( )
答案:D
知识点:点、线、面、体
解析:
解答:将直角三角形绕它的斜边旋转,那么得到的几何体上下应该都有“尖”的部分,所以选择D.
分析:一般的含有曲面的几何体都可以由某一个平面图形旋转得到.
10.如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少需要( )
A.23平方米 B.90平方米 C.130平方米 D.120平方米
答案:B
知识点:几何体的展开图
解析:
解答:地毯的长即楼梯所有台阶的高度与宽度的和即(8+10)米,地毯的宽即台阶的长即5米,所以这块地毯的面积至少为90平方米.
分析:题目中的“至少”是指这块地毯在理想的状况下够用.
11.将如图直角△ABC绕直角边BC旋转一周,所得几何体从它的左面看得到平面图形是( )
A B C D
答案:C
知识点:认识立体图形;点、线、面、体
解析:
解答:如图直角△ABC绕直角边BC旋转一周,所得几何体为“放倒”的圆锥体,所以从它的左面看到的是一个圆形,所以选C.
分析:先根据题目判断得到的几何体的图形,再判断从左面看该几何体的平面图形.
12.汽车的雨刷能把玻璃上的雨水刷干净,这说明( )
A.点动成线 B.线动成面 C.面动成体 D.以上说法都不对
答案:B
知识点:点、线、面、体
解析:
解答:雨刷可以看成一条线,在玻璃上刷出的一片区域为面,所以可以说明线动成面.
分析:理论联系实际,深刻的理解点、线、面、体的概念,给出合理的解释.
13.按组成面的平和曲划分,与圆锥为同一类的几何体是( )
A.棱锥 B.棱柱 C.圆锥 D.长方体
答案:C
知识点:认识立体图形
解析:
解答:圆柱、圆锥都是由曲面和平面组成,棱柱、棱锥全部由平面组成,球全部由曲面组成.
分析:圆柱、圆锥与棱柱、棱锥是不同的两类几何体.
14.想一想:将左边的图形折成一个立方体,那么这个立方体是( )
答案:B
知识点:几何体的展开图
解析:
解答:将左边的图形折成一个正方体时,“梅花”的部分应与画线的部分相对应,所以用排除的方法只能选择B.
分析:可以自制一个简单的图形,将其折叠后也可以选出答案.
15.如图所示,下列图形中不是正方体的展开图是( )
答案:C
知识点:几何体的展开图
解析:
解答:C中折叠后不能成为一个正方体,而是有一个底重合,另一个无底的不完整正方体.
分析:正方体的展开图有11中,是练习同学们空间想象的一个很好的素材.
二、填空题
1.笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周形成了一圆锥体,这说明了_____________.
答案:点动成线;线动成面;面动成体
知识点:点、线、面、体
解析:
解答:本题是点、线、面、体间的动态关系在实际生活中理解.
分析:理论联系实际,深刻的理解点、线、面、体的概念,给出合理的解释.
2.如图,三棱锥有________个面,它们相交形成了________条棱, 这些棱相交形成了________个点.
答案:4;6;4
知识点:认识立体图形;点、线、面、体
解析:
解答:三棱锥有4个面,它们相交形成了6条棱, 这些棱相交形成了4个点.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
3.①一段烟囱(无烟囱帽);②一段圆钢;③铅锤;④烟囱帽.①②都呈 的形状;③④都呈 的形状.
答案:圆柱;圆锥
知识点:认识立体图形
解析:
解答:联系生活实际,结合几何体的概念解答本题.
分析:多留心生活中的事物,这类题就很容易解答.
4.如图,观察图形填空;包围着体的是______;面与面相交的地方形成______;线与线相交的地方是_______.
答案:面;线;点
知识点:点、线、面、体
解析:
解答:包围着体的是面,面与面相交的地方形成线,线与线相交的地方是点.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
5.在图中是正方体展开图的有_________.
答案:②④
知识点:几何体的展开图
解析:
解答:①③不能折成正方体.
分析:可以制作题目中所给的展开图,看能否折成正方体.
三、解答题
1.如图,各图中的阴影图形绕着直线I旋转360°,各能形成怎样的立体图形
答案:第一个可以得到圆柱;第二个可以得到圆锥;第三个可以得到球
知识点:点、线、面、体
解析:
解答:解:第一个可以得到圆柱;第二个可以得到圆锥;第三个可以得到球.
分析:圆柱可以看作是由长方形某条边所在的直线旋转得到,圆锥可以看作是由直角三角形绕着一条直角边所在直线旋转得到,球可以看作是由圆绕某条直径所在直线旋转得到.
2.如下图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.
答案:如图所示
知识点:点、线、面、体
解析:
解答:解:如图所示:
分析:这些也都是“面动成体”的体现.
3.如图所示,用字母M表示与A相对的面,请在下面的正方体展开图中填写相应的字母.
答案:如图所示
知识点:几何体的展开图
解析:
解答:解:如图所示:
分析:可以通过模型,动手试一试,可以得到答案.
4.(1)如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.
图形 顶点数 边数 区域数
(1) 4 6 3
(2)
(3)
(4)
(2)观察上表,推断一个平面图形的顶点数,边数,区域数之间有什么关系?
答案:(1)如图所示;(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1
知识点:点、线、面、体
解析:
解答:解:(1)通过观察,填表如下:
图形 顶点数 边数 区域数
(1) 4 6 3
(2) 8 12 5
(3) 6 9 4
(4) 10 15 6
(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1.
分析:可以制作题目中所给的展开图,看能否折成正方体关键是确定好每一个图形的顶点数、区域数和边数,这是寻找规律的基础.
5.图中的几何体由几个面围城?面与面相交成几条线?它们中有几条是直的,几条是曲的?
答案:图中几何体由7个面围城;面与面相交成15条线;它们中有15条是直的,0条是曲的.
知识点:点、线、面、体
解析:
解答:解:图中几何体由7个面围城;面与面相交成15条线;它们中有15条是直的,0条是曲的.
分析:几何图形都是由点、线、面、体组成的,其中点是构成图形的基本元素.
