新人教版数学七年级上册第四章几何图形初步4.3.3《余角和补角》课时练习.doc
文档属性
| 名称 | 新人教版数学七年级上册第四章几何图形初步4.3.3《余角和补角》课时练习.doc |

|
|
| 格式 | doc | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-06 00:00:00 | ||
图片预览


文档简介
新人教版数学七年级上册第四章第三节余角与补角课时练习
一、选择题
1.52°24'的余角和补角分别是( )
A.37°36',127°36' B.127°36',37°36' C.38°24',128°24' D.128°24',38°24'答案:A
知识点:余角和补角 角的计算
解析:
解答:52°24'的余角为:90°-52°24'=89°60'-52°24'=37°36',它的补角为:180°-52°24'=179°60'-52°24'=127°36'.
分析:和为90°的两个角互为余角,和为180°的两个角互为补角.
2.一个角比它的余角大25°,那么这个角的补角是( )
A.67.5° B.22.5° C.57.5° D.122.5°
答案:D
知识点:余角和补角 一元一次方程的应用
解析:
解答:设这个角的度数为x°,根据题意得:x-(90-x)=25,解得x=57.5,所以这个角为57.5°,所以这个角的补角为180°-57.5°=122.5°.
分析:先根据题意利用一元一次方程求的这个角,再根据补角的定义求这个角的补角.
3.∠α的补角与∠β的余角相等,则∠α与∠β的关系是( )
A.互为余角 B.互为补角 C.∠α比∠β大90° D.∠β比∠α大90°
答案:C
知识点:余角和补角 等式的性质
解析:
解答:因为∠α的补角与∠β的余角相等,所以180°-∠α=90°-∠β,等式两边都减90°同时加∠α得90°=∠α-∠β,所以∠α比∠β大90°.
分析:根据余角和补角的定义列等式,再利用等式的性质对所列的等式进行变形,最后找到正确的答案.
4.若∠1和∠2互补,且∠1<∠2,则∠1的余角是( )
A. B. C.∠2—∠1 D.
答案:D
知识点:余角和补角
解析:
解答:因为∠1和∠2互补即∠1+∠2=180°,所以,所以∠1的余角为.
分析:互为补角的两个角有∠1<∠2即∠1为锐角,因为只有直角和锐角有余角,钝角没有余角.
5.已知∠1=30°,则∠1的余角度数( )
A.160° B.150° C.70° D.60°
答案:D
知识点:余角和补角
解析:
解答:因为90°-30°=60°,所以∠1的余角度数60°.
分析:一个角的余角可以有多个,但是它们的度数是相同的.
6.如果和互补,且,则下列表示的余角的式子中正确的有( ) ① ② ③ ④
A.①②③ B.①②④ C.①③④ D.②③④
答案:B
知识点:余角和补角
解析:
解答:因为∠α和∠β互补即∠α+∠β=180°,所以,所以∠β的余角为,所以④正确;根据余角的定义①正确;因为,所以②正确.
分析:互为补角的两个角有即∠β为锐角,因为只有直角和锐角有余角,钝角没有余角.
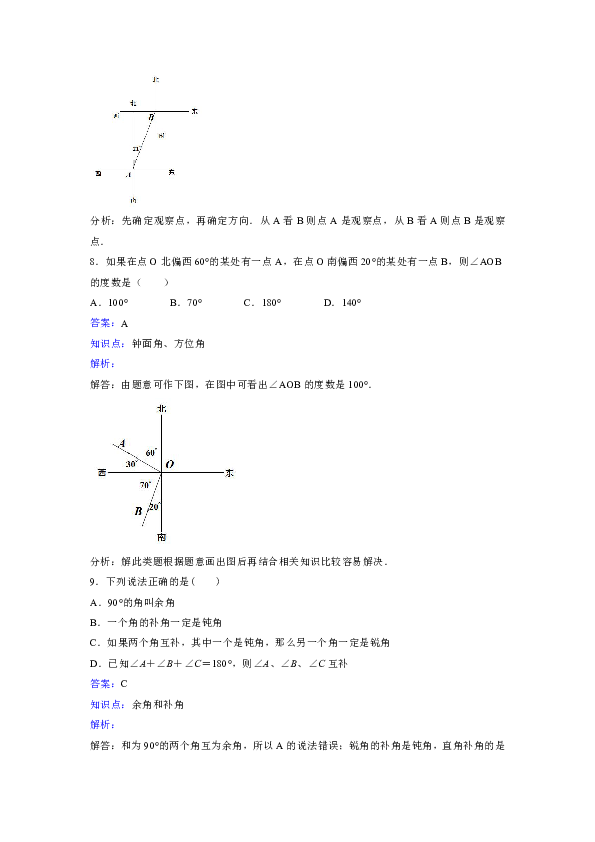
7.A看B的方向是北偏东21°,那么B看A的方向( )
A.南偏东69° B.南偏西69° C.南偏东21° D.南偏西21°
答案:D
知识点:钟面角、方位角
解析:
解答:由题意作图,在图中可知B看A的方向是南偏西21°.
分析:先确定观察点,再确定方向.从A看B则点A是观察点,从B看A则点B是观察点.
8.如果在点O北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
答案:A
知识点:钟面角、方位角
解析:
解答:由题意可作下图,在图中可看出∠AOB的度数是100°.
分析:解此类题根据题意画出图后再结合相关知识比较容易解决.
9.下列说法正确的是( )
A.90°的角叫余角
B.一个角的补角一定是钝角
C.如果两个角互补,其中一个是钝角,那么另一个角一定是锐角
D.已知∠A+∠B+∠C=180°,则∠A、∠B、∠C互补
答案:C
知识点:余角和补角
解析:
解答:和为90°的两个角互为余角,所以A的说法错误;锐角的补角是钝角,直角补角的是直角,钝角的补角是锐角,所以B的说法错误而C的说法正确;互补是两个角之间的数量关系,所以D的说法错误.
分析:紧扣余角和补角的定义来解此类题.
10.如果∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,则∠2与∠4的数量关系是( )
A.∠2=∠4 B.∠2<∠4 C.∠2>∠4 D.无法判断
答案:A
知识点:余角和补角 角的大小比较
解析:
解答:因为∠1与∠2互余,∠3与∠4互余,且∠1=∠3,即等角的余角相等,所以∠2=∠4.
分析:余角的性质:同角(等角)的余角相等.
11.一个锐角的余角加上90°,就等于( )
A.这个锐角的余角 B.这个锐角的补角
C.这个锐角的2倍 D.这个锐角的3倍
答案:B
知识点:余角和补角
解析:
解答:设这个锐角为∠α,那么根据题意有90°-∠α+90°=180°-∠α,即为∠α的补角.
分析:根据余角与补角的定义列式即可解此题.
12.一个角的余角比它本身小,这个角是( )
A.大于45° B.小于45° C.大于0°小于45° D.大于45°小于90°
答案:D
知识点:余角和补角
解析:
解答:依据选项,可以选取度数大于45°的角,如60°的角,发现满足题意,但是只有锐角才有余角,所以必须同时小于90°,所以选择D.
分析:对于单选题和填空题,有时我们可以采用取特殊值的方法解题.
13.下列说法中正确的是( )
A.一个角的补角只有一个
B.一个角的补角必大于这个角
C.若不相等的两个角互补,则这两个角一个是锐角,一个是钝角
D.互余的两个角一定相等
答案:C
知识点:余角和补角
解析:
解答:一个角的补角可以有多个,但是它们的度数相同,所以A的说法错误;一个钝角的补角为锐角,那么它的补角小于这个角,所以B的说法错误;互余的两个角和90°,不一定相等,所以D的说法错误.
分析:锐角的补角为钝角,直角的补角为直角,钝角的补角为锐角.
14.如果一个角等于36°,那么它的余角等于( )
A.64° B.54° C.144° D.36°
答案:B
知识点:余角和补角
解析:
解答:和为90°的两个角互为余角,所以36°的角的余角为54°.
分析:和为90°的两个角互为余角.
15.∠=∠,且∠与∠互余,则( )
A.∠=90° B.∠=45° C.∠=60° D.∠=30°
答案:B
知识点:余角和补角
解析:
解答:因为∠α与∠β互余,所以∠α+∠β=90°,又因为∠α=∠β,所以2∠α=90°即∠α=∠β=45°.
分析:互余的两个角和为90°.
二、填空题
1.40°的余角是 ,106°20'的补角是 .
答案:50°;73°40'
知识点:余角和补角 角的计算
解析:
解答:因为90°-40°=50°,所以40°的余角是50°;因为180°-106°20'=73°40',所以106°20'的补角是73°40'.
分析:互余的两个角和为90°,互补的两个角和为180°.
2.一个角为n°(n<90),则它的余角为 ,补角为 .
答案:90°-n°;180°-n°
知识点:余角和补角
解析:
解答:因为互余的两个角和为90°,所以n°角的余角为90°-n°,又因为互补的两个角和为180°,所以n°角的补角为180°-n°.
分析:互余的两个角和为90°,互补的两个角和为180°.
3.和都是的余角,则 .
答案:=
知识点:余角和补角
解析:
解答:因为∠α和∠β都是∠AOB的余角,又因为同角的余角相等,所以∠α=∠β.
分析:余角的性质:同角(等角)的余角相等.
4.如果∠3+∠4=180°,∠5+∠3=180°,则∠4与∠5的关系是 ,理由是 .
答案:∠4 =∠5;同角的补角相等
知识点:余角和补角
解析:
解答:因为∠3+∠4=180°,∠5+∠3=180°,即∠3与∠4、∠5分别互补,所以∠4=∠5,理由为同角的补角相等.
分析:补角的性质:同角(等角)的补角相等.
5.看下图填空:
∠AOB=∠AOD-( )=( )-∠BOC;
∠COD=∠BOD-( )=∠AOD-( ).
( http: / / www.21cnjy.com )
答案:∠BOD,∠AOC;∠BOC,∠AOC
知识点:角的计算
解析:
解答:结合图形可解此题.
分析:在进行角的和、差运算时,一定要结合图形,只有先弄清角之间的位置关系,才能正确解题.
三、解答题
1.读句画图并填空:
(1)画平角AOB,画射线OC,再分别画、的角平分线OD、OE;
(2)图中,∵ , ,
∴ = ×= .
答案:(1)见解析图;(2)
知识点:角平分线的定义
解析:
解答:解:(1)如下图所示:
(2)∵,(角平分线的定义)∴=(等量代换).
分析:角平分线即将一个分成两个相等角的射线.
2.和互补,且,求和的度数.
答案:115°,65°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:设∠α的度数为x,则∠β的度数为180°-x.因为∠α-∠β=50°,所以x-(180°-x)=50°,解得x=115°,所以∠β=65°,所以∠α和∠β的度数分别为115°和65°.
分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.
3.一个角的余角比它的补角的还少,求这个角的度数.
答案:75°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:设这个角的度数为x.根据题意得90°-x=(180°-x)-20°,解得x=75°,所以这个角的度数为75°.
分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.
4.若和互余,且:=7:2,求、的度数.
答案:70°,20°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:因为∠α:∠β=7:2,所以可设∠α和∠β的度数分别为7x与2x.因为∠α和∠β互余,所以7x+2x=90°,解得x=10°,所以∠α=70°,∠β=20°,所以∠α与∠β的度数分别为70°与20°.
分析:在遇到比例时,我们一般设一份为x.
5.如图,已知,比大,OB是的平分线,求的度数.
答案:14°
知识点:余角和补角 角平分线的定义 一元一次方程的应用 角的计算
解析:
解答:解:设∠AOD的度数为x,则∠COD的度数为x+28°.因为∠AOC=90°,所以可列方程x+x+28°=90°,解得x=31°,即∠AOD=31°,又因为OB是∠AOC的平分线,所以∠AOB=45°,所以∠BOD=∠BOA-∠AOD=45-31°=14°.
分析:求∠BOD,由图中可知∠BOD=∠BOA-∠AOD,由题可知关键在于求∠AOD,所以可设∠AOD的度数为x,则∠COD的度数为x+28°,再结合题意与图形可知∠COD与∠AOD互余可列方程,进而求得∠AOD,最后求得∠BOD.
一、选择题
1.52°24'的余角和补角分别是( )
A.37°36',127°36' B.127°36',37°36' C.38°24',128°24' D.128°24',38°24'答案:A
知识点:余角和补角 角的计算
解析:
解答:52°24'的余角为:90°-52°24'=89°60'-52°24'=37°36',它的补角为:180°-52°24'=179°60'-52°24'=127°36'.
分析:和为90°的两个角互为余角,和为180°的两个角互为补角.
2.一个角比它的余角大25°,那么这个角的补角是( )
A.67.5° B.22.5° C.57.5° D.122.5°
答案:D
知识点:余角和补角 一元一次方程的应用
解析:
解答:设这个角的度数为x°,根据题意得:x-(90-x)=25,解得x=57.5,所以这个角为57.5°,所以这个角的补角为180°-57.5°=122.5°.
分析:先根据题意利用一元一次方程求的这个角,再根据补角的定义求这个角的补角.
3.∠α的补角与∠β的余角相等,则∠α与∠β的关系是( )
A.互为余角 B.互为补角 C.∠α比∠β大90° D.∠β比∠α大90°
答案:C
知识点:余角和补角 等式的性质
解析:
解答:因为∠α的补角与∠β的余角相等,所以180°-∠α=90°-∠β,等式两边都减90°同时加∠α得90°=∠α-∠β,所以∠α比∠β大90°.
分析:根据余角和补角的定义列等式,再利用等式的性质对所列的等式进行变形,最后找到正确的答案.
4.若∠1和∠2互补,且∠1<∠2,则∠1的余角是( )
A. B. C.∠2—∠1 D.
答案:D
知识点:余角和补角
解析:
解答:因为∠1和∠2互补即∠1+∠2=180°,所以,所以∠1的余角为.
分析:互为补角的两个角有∠1<∠2即∠1为锐角,因为只有直角和锐角有余角,钝角没有余角.
5.已知∠1=30°,则∠1的余角度数( )
A.160° B.150° C.70° D.60°
答案:D
知识点:余角和补角
解析:
解答:因为90°-30°=60°,所以∠1的余角度数60°.
分析:一个角的余角可以有多个,但是它们的度数是相同的.
6.如果和互补,且,则下列表示的余角的式子中正确的有( ) ① ② ③ ④
A.①②③ B.①②④ C.①③④ D.②③④
答案:B
知识点:余角和补角
解析:
解答:因为∠α和∠β互补即∠α+∠β=180°,所以,所以∠β的余角为,所以④正确;根据余角的定义①正确;因为,所以②正确.
分析:互为补角的两个角有即∠β为锐角,因为只有直角和锐角有余角,钝角没有余角.
7.A看B的方向是北偏东21°,那么B看A的方向( )
A.南偏东69° B.南偏西69° C.南偏东21° D.南偏西21°
答案:D
知识点:钟面角、方位角
解析:
解答:由题意作图,在图中可知B看A的方向是南偏西21°.
分析:先确定观察点,再确定方向.从A看B则点A是观察点,从B看A则点B是观察点.
8.如果在点O北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
答案:A
知识点:钟面角、方位角
解析:
解答:由题意可作下图,在图中可看出∠AOB的度数是100°.
分析:解此类题根据题意画出图后再结合相关知识比较容易解决.
9.下列说法正确的是( )
A.90°的角叫余角
B.一个角的补角一定是钝角
C.如果两个角互补,其中一个是钝角,那么另一个角一定是锐角
D.已知∠A+∠B+∠C=180°,则∠A、∠B、∠C互补
答案:C
知识点:余角和补角
解析:
解答:和为90°的两个角互为余角,所以A的说法错误;锐角的补角是钝角,直角补角的是直角,钝角的补角是锐角,所以B的说法错误而C的说法正确;互补是两个角之间的数量关系,所以D的说法错误.
分析:紧扣余角和补角的定义来解此类题.
10.如果∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,则∠2与∠4的数量关系是( )
A.∠2=∠4 B.∠2<∠4 C.∠2>∠4 D.无法判断
答案:A
知识点:余角和补角 角的大小比较
解析:
解答:因为∠1与∠2互余,∠3与∠4互余,且∠1=∠3,即等角的余角相等,所以∠2=∠4.
分析:余角的性质:同角(等角)的余角相等.
11.一个锐角的余角加上90°,就等于( )
A.这个锐角的余角 B.这个锐角的补角
C.这个锐角的2倍 D.这个锐角的3倍
答案:B
知识点:余角和补角
解析:
解答:设这个锐角为∠α,那么根据题意有90°-∠α+90°=180°-∠α,即为∠α的补角.
分析:根据余角与补角的定义列式即可解此题.
12.一个角的余角比它本身小,这个角是( )
A.大于45° B.小于45° C.大于0°小于45° D.大于45°小于90°
答案:D
知识点:余角和补角
解析:
解答:依据选项,可以选取度数大于45°的角,如60°的角,发现满足题意,但是只有锐角才有余角,所以必须同时小于90°,所以选择D.
分析:对于单选题和填空题,有时我们可以采用取特殊值的方法解题.
13.下列说法中正确的是( )
A.一个角的补角只有一个
B.一个角的补角必大于这个角
C.若不相等的两个角互补,则这两个角一个是锐角,一个是钝角
D.互余的两个角一定相等
答案:C
知识点:余角和补角
解析:
解答:一个角的补角可以有多个,但是它们的度数相同,所以A的说法错误;一个钝角的补角为锐角,那么它的补角小于这个角,所以B的说法错误;互余的两个角和90°,不一定相等,所以D的说法错误.
分析:锐角的补角为钝角,直角的补角为直角,钝角的补角为锐角.
14.如果一个角等于36°,那么它的余角等于( )
A.64° B.54° C.144° D.36°
答案:B
知识点:余角和补角
解析:
解答:和为90°的两个角互为余角,所以36°的角的余角为54°.
分析:和为90°的两个角互为余角.
15.∠=∠,且∠与∠互余,则( )
A.∠=90° B.∠=45° C.∠=60° D.∠=30°
答案:B
知识点:余角和补角
解析:
解答:因为∠α与∠β互余,所以∠α+∠β=90°,又因为∠α=∠β,所以2∠α=90°即∠α=∠β=45°.
分析:互余的两个角和为90°.
二、填空题
1.40°的余角是 ,106°20'的补角是 .
答案:50°;73°40'
知识点:余角和补角 角的计算
解析:
解答:因为90°-40°=50°,所以40°的余角是50°;因为180°-106°20'=73°40',所以106°20'的补角是73°40'.
分析:互余的两个角和为90°,互补的两个角和为180°.
2.一个角为n°(n<90),则它的余角为 ,补角为 .
答案:90°-n°;180°-n°
知识点:余角和补角
解析:
解答:因为互余的两个角和为90°,所以n°角的余角为90°-n°,又因为互补的两个角和为180°,所以n°角的补角为180°-n°.
分析:互余的两个角和为90°,互补的两个角和为180°.
3.和都是的余角,则 .
答案:=
知识点:余角和补角
解析:
解答:因为∠α和∠β都是∠AOB的余角,又因为同角的余角相等,所以∠α=∠β.
分析:余角的性质:同角(等角)的余角相等.
4.如果∠3+∠4=180°,∠5+∠3=180°,则∠4与∠5的关系是 ,理由是 .
答案:∠4 =∠5;同角的补角相等
知识点:余角和补角
解析:
解答:因为∠3+∠4=180°,∠5+∠3=180°,即∠3与∠4、∠5分别互补,所以∠4=∠5,理由为同角的补角相等.
分析:补角的性质:同角(等角)的补角相等.
5.看下图填空:
∠AOB=∠AOD-( )=( )-∠BOC;
∠COD=∠BOD-( )=∠AOD-( ).
( http: / / www.21cnjy.com )
答案:∠BOD,∠AOC;∠BOC,∠AOC
知识点:角的计算
解析:
解答:结合图形可解此题.
分析:在进行角的和、差运算时,一定要结合图形,只有先弄清角之间的位置关系,才能正确解题.
三、解答题
1.读句画图并填空:
(1)画平角AOB,画射线OC,再分别画、的角平分线OD、OE;
(2)图中,∵ , ,
∴ = ×= .
答案:(1)见解析图;(2)
知识点:角平分线的定义
解析:
解答:解:(1)如下图所示:
(2)∵,(角平分线的定义)∴=(等量代换).
分析:角平分线即将一个分成两个相等角的射线.
2.和互补,且,求和的度数.
答案:115°,65°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:设∠α的度数为x,则∠β的度数为180°-x.因为∠α-∠β=50°,所以x-(180°-x)=50°,解得x=115°,所以∠β=65°,所以∠α和∠β的度数分别为115°和65°.
分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.
3.一个角的余角比它的补角的还少,求这个角的度数.
答案:75°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:设这个角的度数为x.根据题意得90°-x=(180°-x)-20°,解得x=75°,所以这个角的度数为75°.
分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.
4.若和互余,且:=7:2,求、的度数.
答案:70°,20°
知识点:余角与补角 一元一次方程的应用
解析:
解答:解:因为∠α:∠β=7:2,所以可设∠α和∠β的度数分别为7x与2x.因为∠α和∠β互余,所以7x+2x=90°,解得x=10°,所以∠α=70°,∠β=20°,所以∠α与∠β的度数分别为70°与20°.
分析:在遇到比例时,我们一般设一份为x.
5.如图,已知,比大,OB是的平分线,求的度数.
答案:14°
知识点:余角和补角 角平分线的定义 一元一次方程的应用 角的计算
解析:
解答:解:设∠AOD的度数为x,则∠COD的度数为x+28°.因为∠AOC=90°,所以可列方程x+x+28°=90°,解得x=31°,即∠AOD=31°,又因为OB是∠AOC的平分线,所以∠AOB=45°,所以∠BOD=∠BOA-∠AOD=45-31°=14°.
分析:求∠BOD,由图中可知∠BOD=∠BOA-∠AOD,由题可知关键在于求∠AOD,所以可设∠AOD的度数为x,则∠COD的度数为x+28°,再结合题意与图形可知∠COD与∠AOD互余可列方程,进而求得∠AOD,最后求得∠BOD.
