简单的线性规划问题(2)-关于整点问题(浙江省台州市)
文档属性
| 名称 | 简单的线性规划问题(2)-关于整点问题(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 33.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-28 19:29:00 | ||
图片预览



文档简介
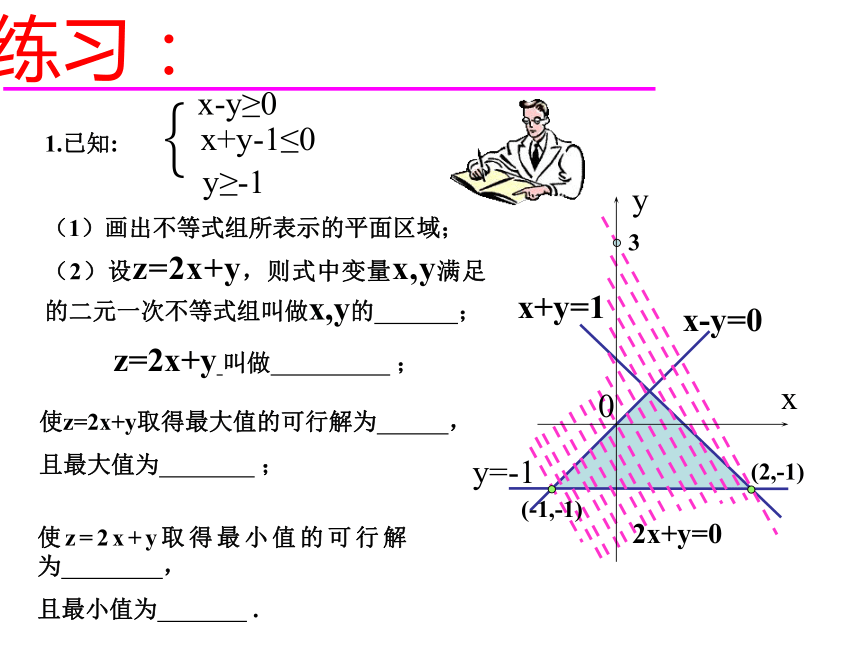
课件8张PPT。简单的线性规划(2)——整点问题使z=2x+y取得最大值的可行解为 ,
且最大值为 ;练习:1.已知:(1)画出不等式组所表示的平面区域;z=2x+y 叫做 ;(2)设z=2x+y,则式中变量x,y满足的二元一次不等式组叫做x,y的 ;y=-1x-y=0x+y=12x+y=0(-1,-1)(2,-1)3使z=2x+y取得最小值的可行解为 ,
且最小值为 .已知:使z=2x-y取得最小值的可行解 ,
且最小值为 .最大值为____________变式:例2、 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 解:设需截第一种钢板x张,第一种钢板y张,则 目标函数为 z=x+y今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。2x+y=15x+3y=27x+2y=18x+y =0作出一组平行直线 z = x+y,目标函数
z= x+y法一:打网格线法在可行域内打出网格线,当直线经过点A时 z=x+y=11.4,但它不是最优整数解,将直线x+y=11.4继续向上平移,经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.作出可行域2x+y=15x+3y=27x+2y=18x+y =0直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解. 作出一组平行直线 z= x+y,当直线经过点A时 z=x+y=11.4,但它不是最优整数解.作直线x+y=12,目标函数
z= x+yx+y=12解得交点B,C的坐标B(3,9)和C(4,8) .二、调整优值法:不等式组:表示的平面区域的整点坐标是:
___________练习:求不等式组所表示的平面区域内的整点坐标练习:
且最大值为 ;练习:1.已知:(1)画出不等式组所表示的平面区域;z=2x+y 叫做 ;(2)设z=2x+y,则式中变量x,y满足的二元一次不等式组叫做x,y的 ;y=-1x-y=0x+y=12x+y=0(-1,-1)(2,-1)3使z=2x+y取得最小值的可行解为 ,
且最小值为 .已知:使z=2x-y取得最小值的可行解 ,
且最小值为 .最大值为____________变式:例2、 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 解:设需截第一种钢板x张,第一种钢板y张,则 目标函数为 z=x+y今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。2x+y=15x+3y=27x+2y=18x+y =0作出一组平行直线 z = x+y,目标函数
z= x+y法一:打网格线法在可行域内打出网格线,当直线经过点A时 z=x+y=11.4,但它不是最优整数解,将直线x+y=11.4继续向上平移,经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.作出可行域2x+y=15x+3y=27x+2y=18x+y =0直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解. 作出一组平行直线 z= x+y,当直线经过点A时 z=x+y=11.4,但它不是最优整数解.作直线x+y=12,目标函数
z= x+yx+y=12解得交点B,C的坐标B(3,9)和C(4,8) .二、调整优值法:不等式组:表示的平面区域的整点坐标是:
___________练习:求不等式组所表示的平面区域内的整点坐标练习:
