5.3.1平行线的性质
图片预览


文档简介
课件27张PPT。欢迎指导!
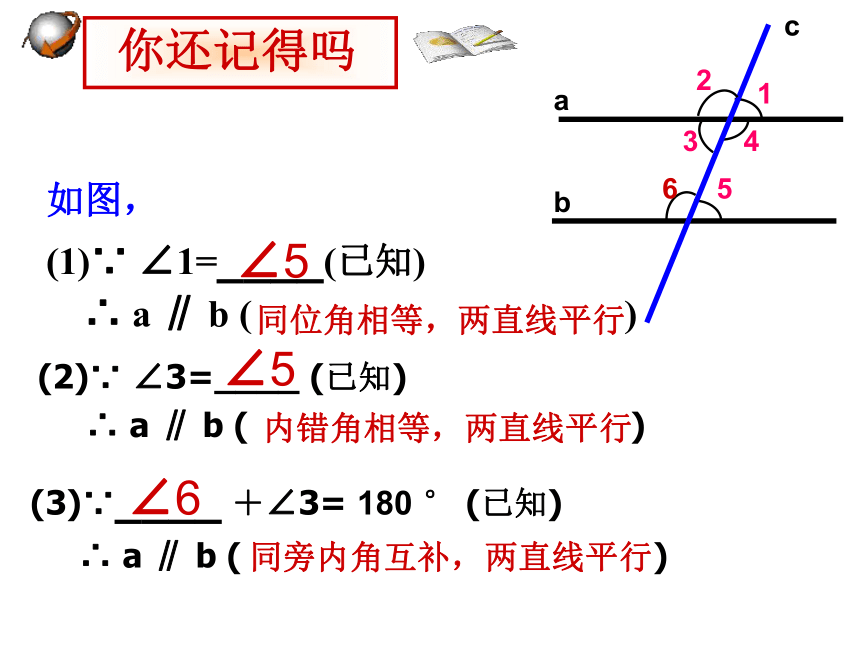
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )(2)∵ ∠3=____ (已知)
∴ a ∥ b (? ) (3)∵____ +∠3= 180 ° (已知)
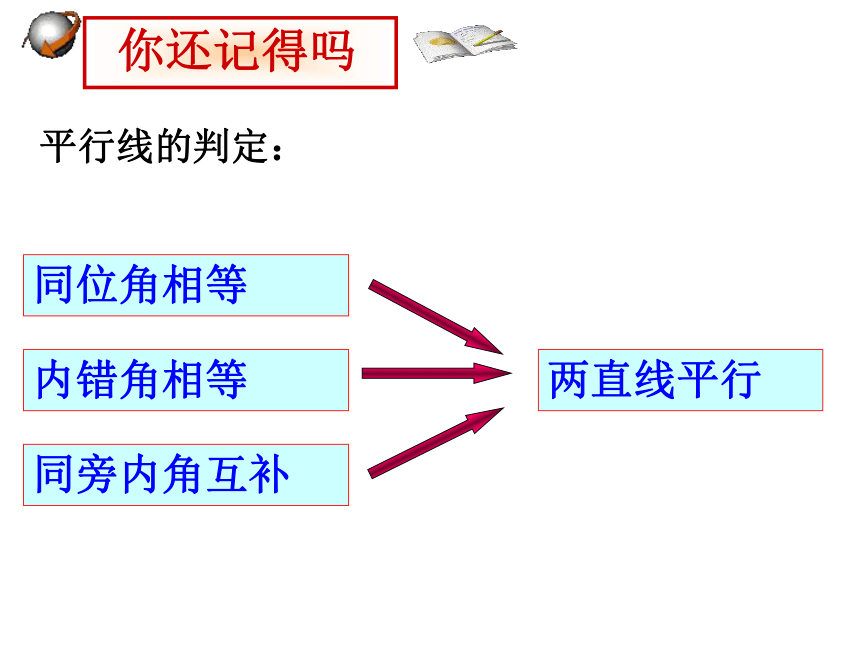
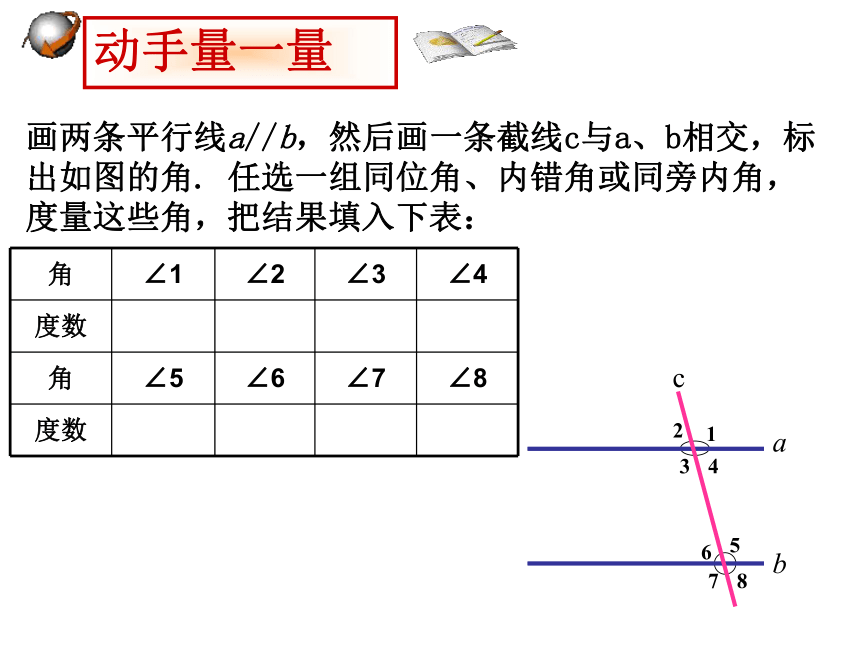
∴ a ∥ b ( ??? )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行cab153426∠5∠5∠6 你还记得吗 你还记得吗同位角相等内错角相等同旁内角互补两直线平行平行线的判定:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:动手量一量 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想: 猜想:
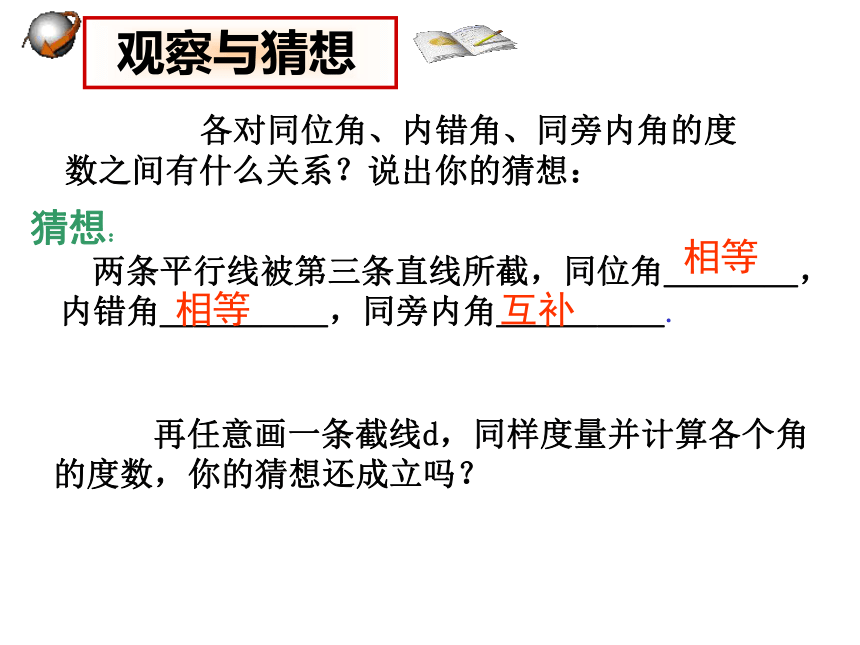
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____. 再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?相等相等互补 观察与猜想平行线的性质: 得出结论性质1:两条平行线被第三条直线所截,同 位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
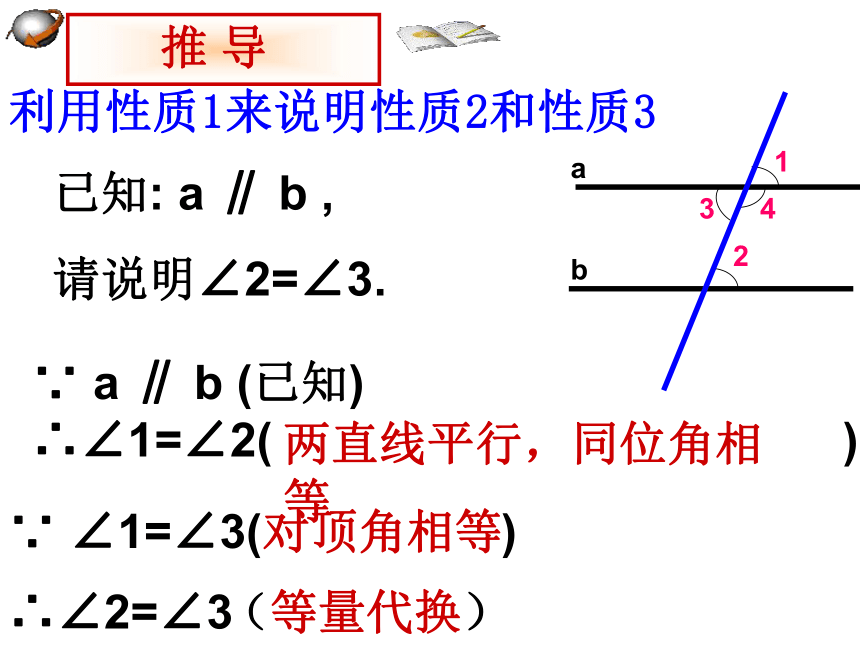
利用性质1来说明性质2和性质3已知: a ∥ b ,
请说明∠2=∠3.∵ a ∥ b (已知)
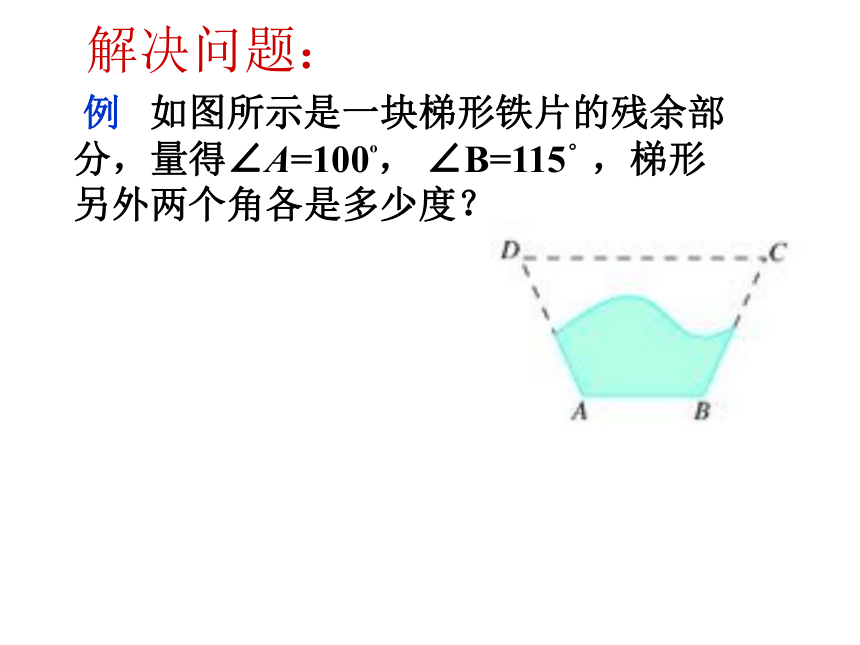
∴∠1=∠2( )∵ ∠1=∠3( )∴∠2=∠3两直线平行,同位角相等对顶角相等(等量代换) 推 导 例 如图所示是一块梯形铁片的残余部分,量得∠A=100o, ∠B=115°,梯形另外两个角各是多少度?解决问题:
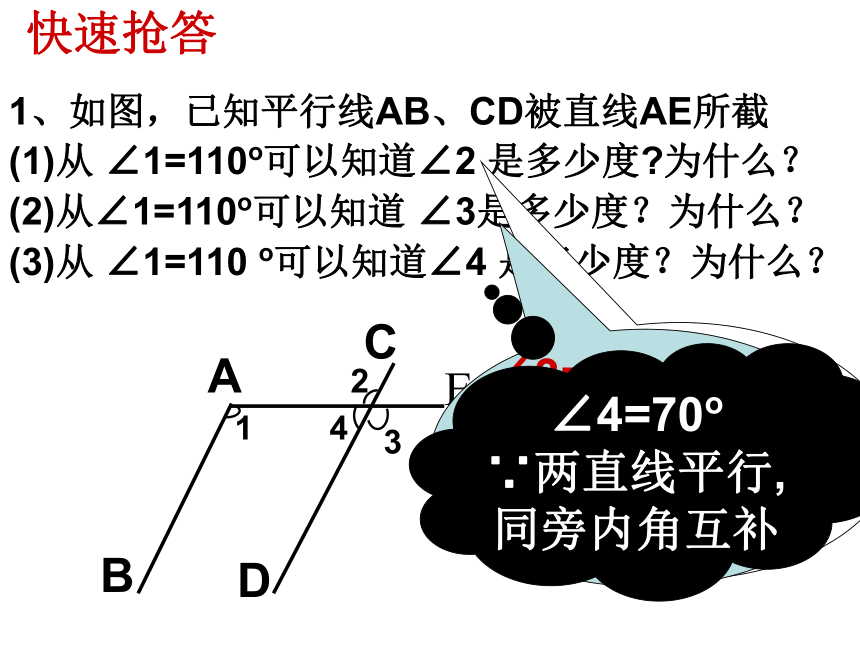
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补快速抢答2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
∠C=142o
∵两直线平行,内错角相等3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗?∟ a⊥b
∵两直线平行, 同位角相等 4、如果有两条直线被第三条直线所截,那么必定有 ( )
(A)内错角相等, (B)同位角相等,(C)同旁内角互补 (D)以上都不对.D巩固练习:
1.如图,直线a∥b, ∠ 1=54o,
那么∠2、∠3、∠4各是多少度?1234答:∠2 = ∠ 1=54o( ),
∠4 = ∠ 1=54o( ),
∠3=180°-∠4
=180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。 (1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.两直线平行,同位角相等两直线平行判定性质(1)请你谈谈本节课的收获小结与回顾:(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补 作业设计:
P23:习题5.3
第2、3、4题请您指导,谢谢!图形已知结果依据同位角内错角同旁内角122324))))))abababccca//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行 小结平行线的性质平行线的判定(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行。两直线平行,同旁内角互补。平行线的性质两直线平行,同位角相等;两直线平行,内错角相等; 两者比较三、选选看2 、∠1 和∠2是两条直线被第三条直线
所截形成的同旁内角,要使这两条直线平
行,必须 ( )
A. ∠1= ∠2 B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o D .∠1是钝角, ∠2是锐角C四、填填看如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。 图1
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知∠CPE两直线平行,同位角相等已知∠CPE两直线平行,同位角相等等量代换 四、填填看如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。图2
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D+ ____=180o ( )
∴∠A+∠D=180o( )
已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 如图。这是一付“角棋”。“棋盘”是一些平行线,“棋子”是用彩纸做成的两个角( ∠1和∠2)。规则如下:从两头开始“跳”角, ∠ 1往下往右跳, ∠ 2往上往右跳,以跳到对方初始位置为胜,双方轮流进行,每“跳”
一步要说出“跳” 的根据(即平行线的性质等),看看谁“跳”得快,理由说得准确。 五、数学游戏12 六、小结发现数学结论的方法:1.数学实验(测量、叠合等)法
2.猜想、推理法1、如图:∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )已知BC∠D内错角相等,两直线平行两直线平行,同旁内角互补 四、填填看平行线的性质:简单说成:
性质1:两直线平行,同位角相
等.
如果a∥b,那么∠1=∠2
性质2:两直线平行,内错角相等.
如果a∥b,那么∠2=∠3
性质3:两直线平行,同旁内角互补.
如果a∥b,那么∠2+∠4=180°
c?31ba
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
?????
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )(2)∵ ∠3=____ (已知)
∴ a ∥ b (? ) (3)∵____ +∠3= 180 ° (已知)
∴ a ∥ b ( ??? )同位角相等,两直线平行内错角相等,两直线平行同旁内角互补,两直线平行cab153426∠5∠5∠6 你还记得吗 你还记得吗同位角相等内错角相等同旁内角互补两直线平行平行线的判定:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:动手量一量 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想: 猜想:
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____. 再任意画一条截线d,同样度量并计算各个角
的度数,你的猜想还成立吗?相等相等互补 观察与猜想平行线的性质: 得出结论性质1:两条平行线被第三条直线所截,同 位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
利用性质1来说明性质2和性质3已知: a ∥ b ,
请说明∠2=∠3.∵ a ∥ b (已知)
∴∠1=∠2( )∵ ∠1=∠3( )∴∠2=∠3两直线平行,同位角相等对顶角相等(等量代换) 推 导 例 如图所示是一块梯形铁片的残余部分,量得∠A=100o, ∠B=115°,梯形另外两个角各是多少度?解决问题:
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补快速抢答2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
∠C=142o
∵两直线平行,内错角相等3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗?∟ a⊥b
∵两直线平行, 同位角相等 4、如果有两条直线被第三条直线所截,那么必定有 ( )
(A)内错角相等, (B)同位角相等,(C)同旁内角互补 (D)以上都不对.D巩固练习:
1.如图,直线a∥b, ∠ 1=54o,
那么∠2、∠3、∠4各是多少度?1234答:∠2 = ∠ 1=54o( ),
∠4 = ∠ 1=54o( ),
∠3=180°-∠4
=180°-54°=126°( ) 对顶角相等两直线平行,同位角相等邻补角的定义2.如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°。 (1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
因为∠ADE=60°,∠B=60°,
所以∠ADE= ∠B.
所以DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
因为DE∥BC ,
所以∠C = ∠AED.( )
因为∠AED=40°,所以∠C =40°.两直线平行,同位角相等两直线平行判定性质(1)请你谈谈本节课的收获小结与回顾:(2)说说平行线的“判定”与“性质”有什么不同?
同位角相等
内错角相等
同旁内角互补 作业设计:
P23:习题5.3
第2、3、4题请您指导,谢谢!图形已知结果依据同位角内错角同旁内角122324))))))abababccca//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行 小结平行线的性质平行线的判定(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行。两直线平行,同旁内角互补。平行线的性质两直线平行,同位角相等;两直线平行,内错角相等; 两者比较三、选选看2 、∠1 和∠2是两条直线被第三条直线
所截形成的同旁内角,要使这两条直线平
行,必须 ( )
A. ∠1= ∠2 B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o D .∠1是钝角, ∠2是锐角C四、填填看如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。 图1
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知∠CPE两直线平行,同位角相等已知∠CPE两直线平行,同位角相等等量代换 四、填填看如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。图2
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D+ ____=180o ( )
∴∠A+∠D=180o( )
已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 如图。这是一付“角棋”。“棋盘”是一些平行线,“棋子”是用彩纸做成的两个角( ∠1和∠2)。规则如下:从两头开始“跳”角, ∠ 1往下往右跳, ∠ 2往上往右跳,以跳到对方初始位置为胜,双方轮流进行,每“跳”
一步要说出“跳” 的根据(即平行线的性质等),看看谁“跳”得快,理由说得准确。 五、数学游戏12 六、小结发现数学结论的方法:1.数学实验(测量、叠合等)法
2.猜想、推理法1、如图:∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )已知BC∠D内错角相等,两直线平行两直线平行,同旁内角互补 四、填填看平行线的性质:简单说成:
性质1:两直线平行,同位角相
等.
如果a∥b,那么∠1=∠2
性质2:两直线平行,内错角相等.
如果a∥b,那么∠2=∠3
性质3:两直线平行,同旁内角互补.
如果a∥b,那么∠2+∠4=180°
c?31ba
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
?????
