五年级下册数学人教版长方体和正方体的表面积(课件)(共44张PPT)
文档属性
| 名称 | 五年级下册数学人教版长方体和正方体的表面积(课件)(共44张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:06:02 | ||
图片预览



文档简介
(共44张PPT)
2.长方体和正方体的表面积
一、回顾旧知识
什么是长方体的长、宽、高 什么是正方体的棱长
请指出长方体纸盒的长、宽、高,并说出长方体的特征。指出正方体的棱长并说出正方体的特征。
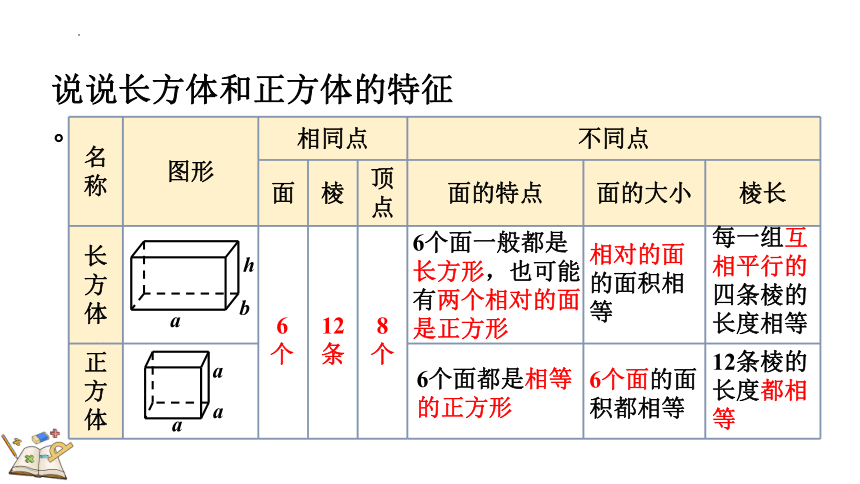
说说长方体和正方体的特征。
名称 图形 相同点 不同点
面 棱 顶点 面的特点 面的大小 棱长
长方体
正方体
6个
12条
8个
6个面一般都是长方形,也可能有两个相对的面是正方形
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
每一组互相平行的四条棱的长度相等
12条棱的长度都相等
a
b
h
a
a
a
二、制作长方体和正方体的展开图
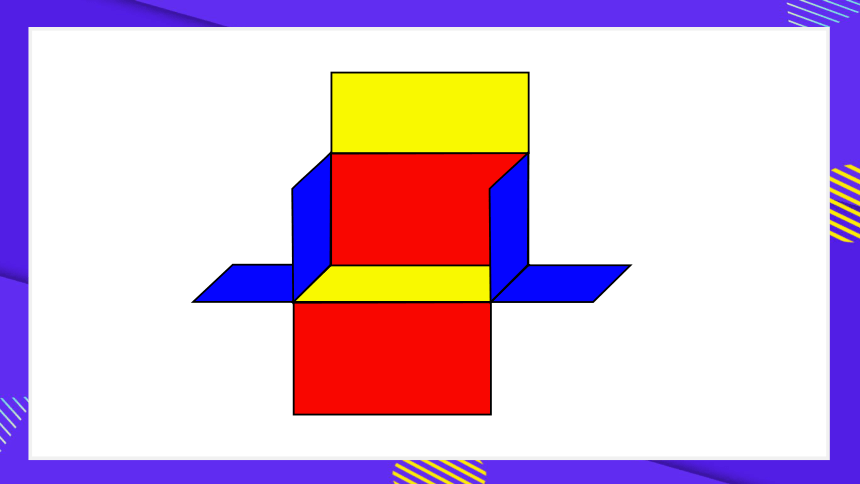
请同学们拿出准备好的长方体纸盒,把它沿着棱剪开,要求剪开后,各面要连接在一起。
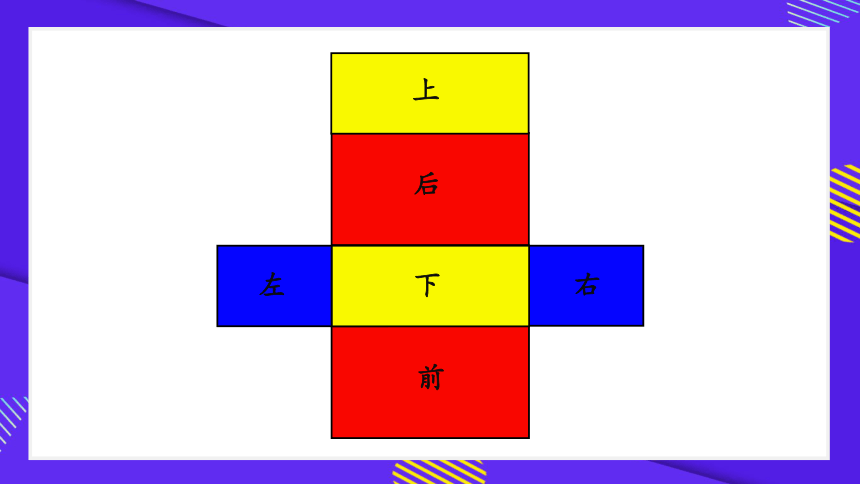
(在展开图中,分别用“上、下、前、后、左、右”标明6个面。)
前
上
下
后
左
右
观察长方体展开图,回答下面的问题:
(1)哪些面的面积相等?
(2)每个面的长和宽与长方体
的长、宽、高有什么关系?
前
上
下
后
左
右
前
上
下
后
左
右
长
高
宽
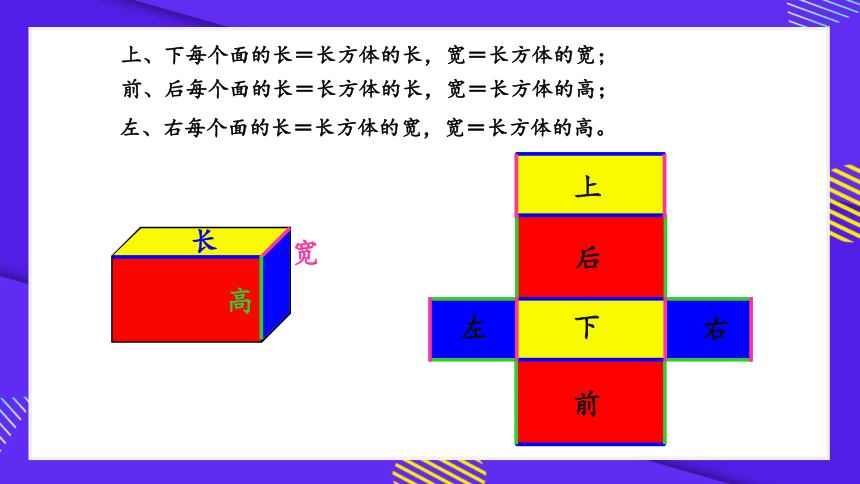
上、下每个面的长=长方体的长,宽=长方体的宽;
前、后每个面的长=长方体的长,宽=长方体的高;
左、右每个面的长=长方体的宽,宽=长方体的高。
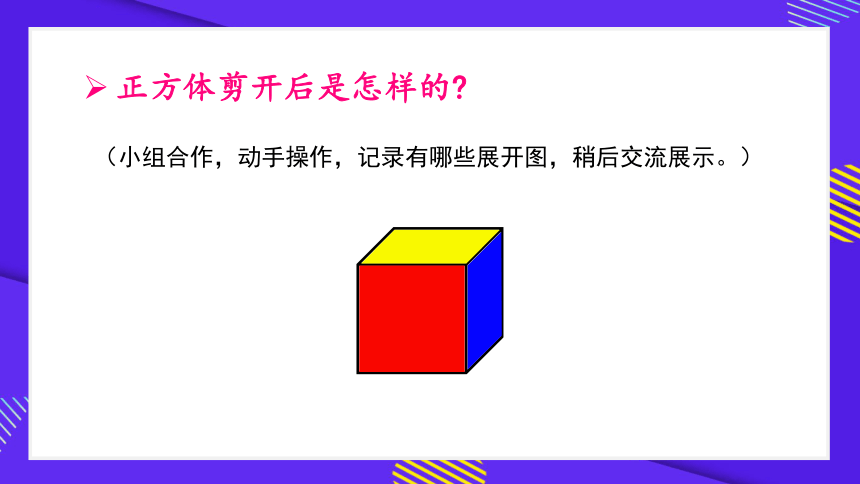
正方体剪开后是怎样的
(小组合作,动手操作,记录有哪些展开图,稍后交流展示。)
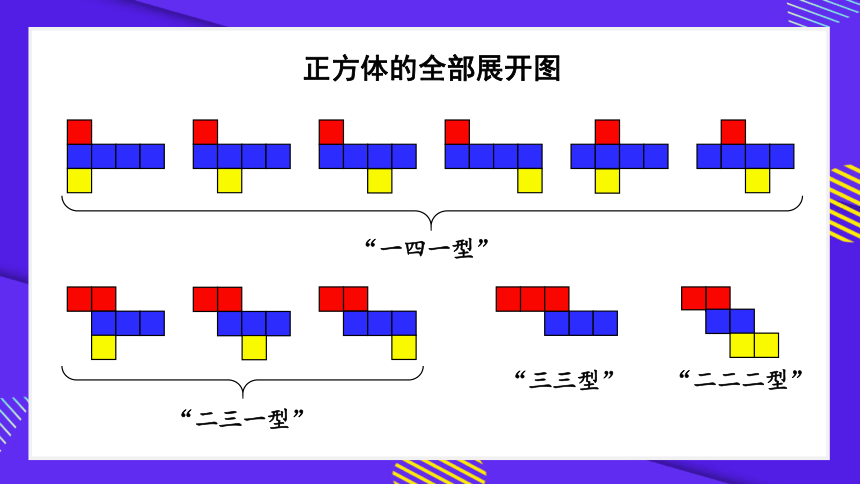
正方体的全部展开图
“一四一型”
“二三一型”
“三三型”
“二二二型”
( )
√
( )
√
( )
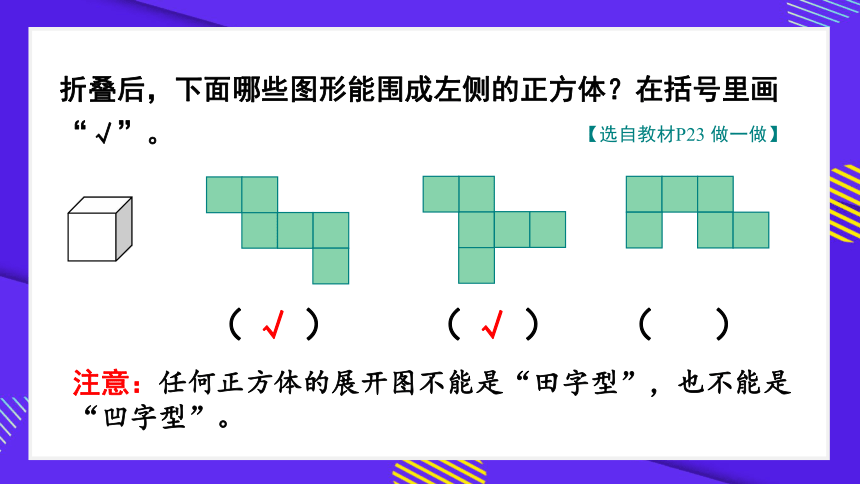
折叠后,下面哪些图形能围成左侧的正方体?在括号里画“√”。
【选自教材P23 做一做】
注意:任何正方体的展开图不能是“田字型”,也不能是“凹字型”。
长方体或正方体 6 个面的面积之和,叫作它的表面积。
三、联系实际,尝试求长方体的表面积
用自己的话说一说什么叫做长方体或者正方体的表面积
制作尺寸如下图所示的长方体和正方体保温箱,各要用多少平方分米的泡沫板 (单位:dm)
读题并思考,先观察长方体保温箱,完成填空部分,再交流汇报。
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
6dm
5dm
30dm2
6dm
4dm
24dm2
5dm
4dm
20m2
请你独立求长方体的表面积,请一位同学上台板演。
长方体的表面积 = 6 个面的面积和
6×5+6×5+6×4+6×4+5×4+5×4
= 30+30+24+24+20+20
= 148(dm2)
方法一
长方体的表面积=上、下两个面的面积 +前、后两个面的面积+左、右两个面的面积
方法二
6×5×2+6×4×2+5×4×2
= 60+48+40
=148(dm2)
方法三
长方体的表面积=(上面的面积+前面的面积+左面的面积)×2
(6×5+6×4+5×4)×2
= 74×2
= 148(dm2)
比较这三种方法,你认为计算长方体的表面积关键是找什么?这三种方法你喜欢哪一种?
长方体的表面积关键是找长方体的长、宽、高。
小组讨论,归纳长方体的表面积计算方法。
长方体的表面积= 长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
a
b
c
S表= 2(ab+ah+bh)
四、独立探究,发现正方体表面积的计算方法
交流讨论后,自主解答例1正方体保温箱需要多少平方分米的泡沫板。稍后展示交流。
想一想:正方体6个面都相同,表面积可以怎样计算?
5×5×6
=25×6
=150(cm2)
正方体的表面积的计算方法是怎样的?
正方体的表面积= 棱长×棱长×6
a
S表=6a2
五、变式练习,巩固应用
1.将下面的展开图围成正方体后,哪两个面分别相对?
春对______
秋对______
暮鼓对______
夏
冬
晨钟
【选自教材P25 练习六 第2题】
2.
(1)计算各长方体中前面的面积。
(2)计算各长方体中右侧面的面积。
(3)计算各长方体中上面的面积。
(4)计算各长方体的表面积。
【选自教材P25 练习六 第3题】
(1)4×2=8(cm2)
2×2=4(cm2)
2.5×2=5(cm2)
(2)3×2=6(cm2)
3×2=6(cm2)
2.5×2=5(cm2)
(3)3×4=12(cm2)
3×2=6(cm2)
2×2=4(cm2)
(4)(8+6+12)×2=52(cm2)
(4+6+6)×2=32(cm2)
(5+5+4)×2=28(cm2)
做一个长 5dm,宽 4dm,高 3dm的长方体布艺收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
= 47×2
= 94(dm2)
答:至少需要 94 平方分米的布。
【选自教材P25 练习六 第4题】
3.
选自教材第24页做一做
0.75×1.6×2+0.5×1.6×2+0.75×0.5
=2.4+1.6+0.375
=4.375(m )
答:至少需要用4.375 m 的布料。
一个长0.75 m、宽0.5 m、高1.6 m的简易衣柜需要换布罩(如图,没有底面)。至少需要用多少平方米布料?
没有底面,这个布罩就只有5个面,要求的就是前、后、左、右面和上面这5个面的面积和。
1.6m
0.75m
0.5m
求下列图形的表面积。
7cm
4cm
5cm
10cm
5cm
8cm
长方体表面积=(长×宽十长×高十宽×高)×2
(7×4+7×5+4×5)×2
=83×2
=166(cm )
(10×5+10×8+5×8)×2
=170×2
=340(cm )
1
如下图,这个正方体有( )个面是正方形,每个面的面积是( )dm ,这个正方体的表面积是( )dm 。
6
25
150
5dm
5dm
5dm
2
长方体的上面不用算,即长×宽算一次即可。
一个无盖的长方体金鱼缸,长是9分米,宽是6分米,高是7分米。做这样的一个鱼缸需要多大面积的玻璃?
9×6+(9×7+6×7)×2
=54+105×2
=54+210
=264(平方分米)
答:做这样的一个鱼缸需要264平方分米的玻璃。
3
8×4×4+4×4×2
=160(cm )
如何把这个长方体木块分成两个棱长为4cm的正方体?
4×4×6×2=192(cm )
这两个的正方体的表面积之和与原长方体的表面积相等吗?
不相等
4
把长方体(或正方体)垂直切割成几部分,它们的表面积会增加,增加的面积等于切面面积的2倍。
六、课堂小结
请举例说说,生活中什么情况下会用到长方体或正方体的表面积知识?
请你整理本节课所学内容。
这节课有什么收获呢?
1.长方体和正方体展开图的形状不是唯一的,展开的方法不同,得到的展开图不相同。但不管怎样展开,相对的两个面不可能相邻。
2.借助长方体和正方体的展开图可以探究各个面之间的关系。
长方体或正方体 6 个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S表= 2(ab+ah+bh)
正方体表面积=棱长×棱长×6
S表=6a2
长方体和正方体的表面积
七、作业设计
完成课时练本课时内容及以下练习题
一、计算下面长方体和正方体的表面积。
上、下每个面的面积是:___________________
前、后每个面的面积是:___________________
左、右每个面的面积是:___________________
长方体的表面积是:_________________或_____________
20×10=200(cm2)
20×8=160(cm2)
10×8=80(cm2)
200×2+ 160×2+ 80×2=880(cm2)
(200+ 160+ 80)×2=880(cm2)
1.
2.
每个面的面积是:___________________
正方体的表面积是:_________________
8×8=64(cm2)
64×6=384(cm2)
3. 一个长方体长6 cm,宽5 cm,高4 cm,这个长方体的表
面积是( )cm2。
148
一个长方体礼品盒,长 20 cm,宽 12 cm,高 8 cm,如果包装这个礼品盒的用纸是其表面积的 1.2 倍,至少要用多少平方厘米的包装纸?
(20×12+20×8+12×8)×2 =992(cm2)
992×1.2 =1190.4(cm2)
答:至少要用1190.4平方厘米的包装纸。
二、
2.长方体和正方体的表面积
一、回顾旧知识
什么是长方体的长、宽、高 什么是正方体的棱长
请指出长方体纸盒的长、宽、高,并说出长方体的特征。指出正方体的棱长并说出正方体的特征。
说说长方体和正方体的特征。
名称 图形 相同点 不同点
面 棱 顶点 面的特点 面的大小 棱长
长方体
正方体
6个
12条
8个
6个面一般都是长方形,也可能有两个相对的面是正方形
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
每一组互相平行的四条棱的长度相等
12条棱的长度都相等
a
b
h
a
a
a
二、制作长方体和正方体的展开图
请同学们拿出准备好的长方体纸盒,把它沿着棱剪开,要求剪开后,各面要连接在一起。
(在展开图中,分别用“上、下、前、后、左、右”标明6个面。)
前
上
下
后
左
右
观察长方体展开图,回答下面的问题:
(1)哪些面的面积相等?
(2)每个面的长和宽与长方体
的长、宽、高有什么关系?
前
上
下
后
左
右
前
上
下
后
左
右
长
高
宽
上、下每个面的长=长方体的长,宽=长方体的宽;
前、后每个面的长=长方体的长,宽=长方体的高;
左、右每个面的长=长方体的宽,宽=长方体的高。
正方体剪开后是怎样的
(小组合作,动手操作,记录有哪些展开图,稍后交流展示。)
正方体的全部展开图
“一四一型”
“二三一型”
“三三型”
“二二二型”
( )
√
( )
√
( )
折叠后,下面哪些图形能围成左侧的正方体?在括号里画“√”。
【选自教材P23 做一做】
注意:任何正方体的展开图不能是“田字型”,也不能是“凹字型”。
长方体或正方体 6 个面的面积之和,叫作它的表面积。
三、联系实际,尝试求长方体的表面积
用自己的话说一说什么叫做长方体或者正方体的表面积
制作尺寸如下图所示的长方体和正方体保温箱,各要用多少平方分米的泡沫板 (单位:dm)
读题并思考,先观察长方体保温箱,完成填空部分,再交流汇报。
上、下每个面,长_____,宽_____,面积是_______;
前、后每个面,长_____,宽_____,面积是_______;
左、右每个面,长_____,宽_____,面积是_______。
6dm
5dm
30dm2
6dm
4dm
24dm2
5dm
4dm
20m2
请你独立求长方体的表面积,请一位同学上台板演。
长方体的表面积 = 6 个面的面积和
6×5+6×5+6×4+6×4+5×4+5×4
= 30+30+24+24+20+20
= 148(dm2)
方法一
长方体的表面积=上、下两个面的面积 +前、后两个面的面积+左、右两个面的面积
方法二
6×5×2+6×4×2+5×4×2
= 60+48+40
=148(dm2)
方法三
长方体的表面积=(上面的面积+前面的面积+左面的面积)×2
(6×5+6×4+5×4)×2
= 74×2
= 148(dm2)
比较这三种方法,你认为计算长方体的表面积关键是找什么?这三种方法你喜欢哪一种?
长方体的表面积关键是找长方体的长、宽、高。
小组讨论,归纳长方体的表面积计算方法。
长方体的表面积= 长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
a
b
c
S表= 2(ab+ah+bh)
四、独立探究,发现正方体表面积的计算方法
交流讨论后,自主解答例1正方体保温箱需要多少平方分米的泡沫板。稍后展示交流。
想一想:正方体6个面都相同,表面积可以怎样计算?
5×5×6
=25×6
=150(cm2)
正方体的表面积的计算方法是怎样的?
正方体的表面积= 棱长×棱长×6
a
S表=6a2
五、变式练习,巩固应用
1.将下面的展开图围成正方体后,哪两个面分别相对?
春对______
秋对______
暮鼓对______
夏
冬
晨钟
【选自教材P25 练习六 第2题】
2.
(1)计算各长方体中前面的面积。
(2)计算各长方体中右侧面的面积。
(3)计算各长方体中上面的面积。
(4)计算各长方体的表面积。
【选自教材P25 练习六 第3题】
(1)4×2=8(cm2)
2×2=4(cm2)
2.5×2=5(cm2)
(2)3×2=6(cm2)
3×2=6(cm2)
2.5×2=5(cm2)
(3)3×4=12(cm2)
3×2=6(cm2)
2×2=4(cm2)
(4)(8+6+12)×2=52(cm2)
(4+6+6)×2=32(cm2)
(5+5+4)×2=28(cm2)
做一个长 5dm,宽 4dm,高 3dm的长方体布艺收纳盒,至少需要多少平方分米的布?
(5×4+5×3+4×3)×2
= 47×2
= 94(dm2)
答:至少需要 94 平方分米的布。
【选自教材P25 练习六 第4题】
3.
选自教材第24页做一做
0.75×1.6×2+0.5×1.6×2+0.75×0.5
=2.4+1.6+0.375
=4.375(m )
答:至少需要用4.375 m 的布料。
一个长0.75 m、宽0.5 m、高1.6 m的简易衣柜需要换布罩(如图,没有底面)。至少需要用多少平方米布料?
没有底面,这个布罩就只有5个面,要求的就是前、后、左、右面和上面这5个面的面积和。
1.6m
0.75m
0.5m
求下列图形的表面积。
7cm
4cm
5cm
10cm
5cm
8cm
长方体表面积=(长×宽十长×高十宽×高)×2
(7×4+7×5+4×5)×2
=83×2
=166(cm )
(10×5+10×8+5×8)×2
=170×2
=340(cm )
1
如下图,这个正方体有( )个面是正方形,每个面的面积是( )dm ,这个正方体的表面积是( )dm 。
6
25
150
5dm
5dm
5dm
2
长方体的上面不用算,即长×宽算一次即可。
一个无盖的长方体金鱼缸,长是9分米,宽是6分米,高是7分米。做这样的一个鱼缸需要多大面积的玻璃?
9×6+(9×7+6×7)×2
=54+105×2
=54+210
=264(平方分米)
答:做这样的一个鱼缸需要264平方分米的玻璃。
3
8×4×4+4×4×2
=160(cm )
如何把这个长方体木块分成两个棱长为4cm的正方体?
4×4×6×2=192(cm )
这两个的正方体的表面积之和与原长方体的表面积相等吗?
不相等
4
把长方体(或正方体)垂直切割成几部分,它们的表面积会增加,增加的面积等于切面面积的2倍。
六、课堂小结
请举例说说,生活中什么情况下会用到长方体或正方体的表面积知识?
请你整理本节课所学内容。
这节课有什么收获呢?
1.长方体和正方体展开图的形状不是唯一的,展开的方法不同,得到的展开图不相同。但不管怎样展开,相对的两个面不可能相邻。
2.借助长方体和正方体的展开图可以探究各个面之间的关系。
长方体或正方体 6 个面的总面积,叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2
S表= 2(ab+ah+bh)
正方体表面积=棱长×棱长×6
S表=6a2
长方体和正方体的表面积
七、作业设计
完成课时练本课时内容及以下练习题
一、计算下面长方体和正方体的表面积。
上、下每个面的面积是:___________________
前、后每个面的面积是:___________________
左、右每个面的面积是:___________________
长方体的表面积是:_________________或_____________
20×10=200(cm2)
20×8=160(cm2)
10×8=80(cm2)
200×2+ 160×2+ 80×2=880(cm2)
(200+ 160+ 80)×2=880(cm2)
1.
2.
每个面的面积是:___________________
正方体的表面积是:_________________
8×8=64(cm2)
64×6=384(cm2)
3. 一个长方体长6 cm,宽5 cm,高4 cm,这个长方体的表
面积是( )cm2。
148
一个长方体礼品盒,长 20 cm,宽 12 cm,高 8 cm,如果包装这个礼品盒的用纸是其表面积的 1.2 倍,至少要用多少平方厘米的包装纸?
(20×12+20×8+12×8)×2 =992(cm2)
992×1.2 =1190.4(cm2)
答:至少要用1190.4平方厘米的包装纸。
二、
