2023-2024学年人教版七年级数学下册课件 5.1相交线 第1课时 相交线(32张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学下册课件 5.1相交线 第1课时 相交线(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 545.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 17:36:49 | ||
图片预览









文档简介
(共32张PPT)
03
课标要求
01
基础梳理
02
典例探究
课时训练
04
第五章 相交线与平行线
5.1 相交线
第1课时 相交线
课标要求
理解对顶角、邻补角等概念,探索并掌握对顶角相等、邻补角互补的性质.
基础梳理
1.邻补角:
(1)概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为 . 图中还有其他的邻补角:_________________
.
邻补角
∠1和∠4,∠3和∠4,
∠3和∠2
(2)性质:邻补角 .
互补
2.对顶角:
(1)概念:如上图,∠1和∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为 .图中还有其他的对顶角: .
(2)性质:对顶角 .
对顶角
∠2和∠4
相等
基础过关
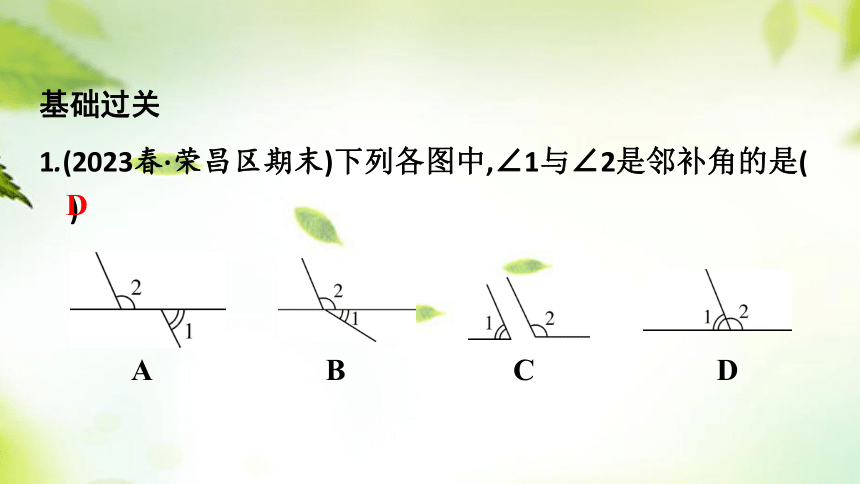
1.(2023春·荣昌区期末)下列各图中,∠1与∠2是邻补角的是( )
A B C D
D
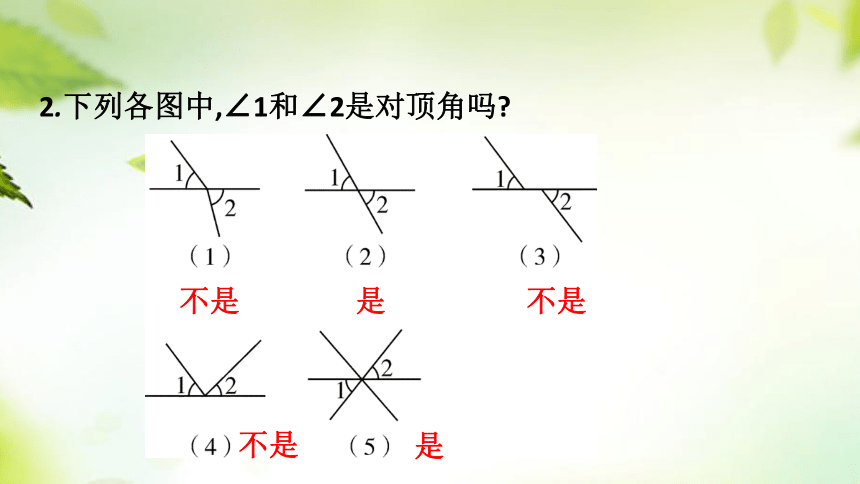
2.下列各图中,∠1和∠2是对顶角吗
不是
是
不是
不是
是
典例探究
知识点1 邻补角、对顶角的定义
【例题1】如图,直线AB,CD相交于点O,OE为以点O为端点的射线,写出图中所有的邻补角和对顶角.
解:互为邻补角的有∠AOE和∠BOE,∠AOD和∠BOD,∠AOC和∠BOC,∠AOC和∠AOD,∠COE和∠DOE,∠BOC和∠BOD.
互为对顶角的有∠AOD和∠BOC,∠AOC和∠BOD.
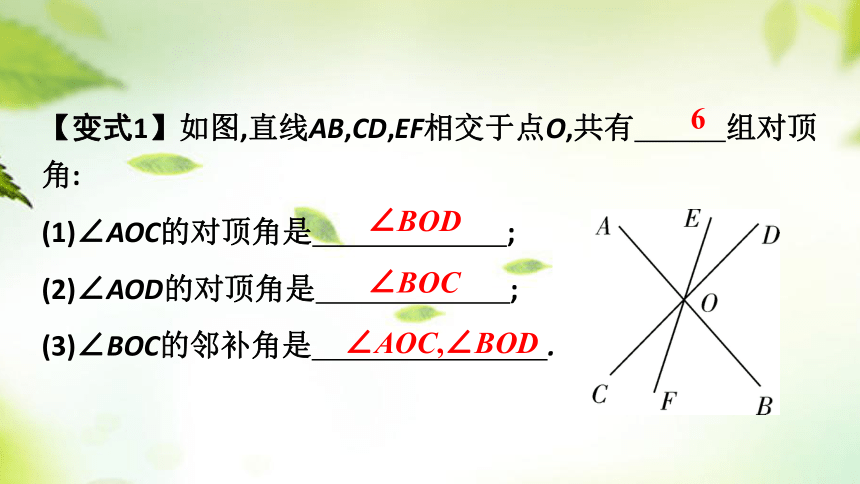
【变式1】如图,直线AB,CD,EF相交于点O,共有 组对顶角:
(1)∠AOC的对顶角是 ;
(2)∠AOD的对顶角是 ;
(3)∠BOC的邻补角是 .
6
∠BOD
∠BOC
∠AOC,∠BOD
知识点2 邻补角、对顶角的性质
【例题2】(2022春·泾阳县期中)如图所示,直线a,b,c两两相交,∠1=∠3+12°,∠2=52°,求∠4的度数.
解:因为∠1与∠2是对顶角,
所以∠1=∠2=52°.
因为∠1=∠3+12°=52°,
所以∠3=40°.
因为∠3与∠4是邻补角,
所以∠4=180°-∠3=180°-40°=140°.
【变式2】如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
解:(1)因为∠1与∠2互为邻补角,
所以∠2=180°-∠1.
因为∠1=50°,
所以∠2=180°-50°=130°.
(2)因为∠1与∠2互为邻补角,
所以∠2+∠1=180°.
因为∠2=3∠1,
所以3∠1+∠1=180°.
解得∠1=45°.
那么∠2=3×45°=135°.
所以∠3=∠1=45°,∠4=∠2=135°.
课时训练
A组
1.(2023春·榆次区期中)如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是 ( )
A.∠2增大4° B.∠3增大4°
C.∠4增大4° D.∠4减小2°
B
2.如图,直线AB,CD相交于点O,OE,OF为过点O的射线,则对顶角有 ( )
A.1对
B.2对
C.3对
D.4对
B
3.∠1与∠2是对顶角,∠2与∠3是邻补角.若∠1=35°,则∠3的大小是 ( )
A.35° B.55° C.125° D.145°
D
4.(2022春·夏邑县期中)如图,直线AB与CD相交于点O,
∠AOC-2∠AOE=20°,射线OF平分∠DOE,若∠BOD=60°,则∠AOF的度数为 ( )
A.50° B.60°
C.70° D.80°
第4题图
C
5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于 ( )
A.38° B.104°
C.142° D.144°
第5题图
C
6.如图,三条直线AB,CD,EF两两相交,在这个图形中,有对顶角 对,邻补角 对.
第6题图
6
12
7.如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是∠BOC,∠AOC的邻补角是 , ;若∠AOC=50°,则∠BOD= ,∠COB= .
第7题图
∠AOD
∠BOC
50°
130°
8.(2022春·胶州市期中)如图,两条直线相交于点O,若∠1+∠2=68°,则∠1= .
34°
9.如图,直线AB,CD,EF相交于点O.
(1)请写出∠AOC,∠AOE,∠EOC的对顶角;
(2)若∠AOC=50°,求∠BOD,∠BOC的度数.
解:(1)∠AOC的对顶角是∠BOD,∠AOE的对顶角是∠BOF,∠EOC的对顶角是∠DOF.
(2)因为∠AOC=50°,
所以∠BOD=50°,∠BOC=180°-50°=130°.
B组
10.(2022春·关岭县期末)如图,直线AB,CD相交于点O,OE是∠BOC的平分线,若∠BOC∶∠AOC=1∶5.求∠BOE的度数.
解:因为∠BOC∶∠AOC=1∶5,
设∠BOC=x,则∠AOC=5x,
因为∠BOC+∠AOC=180°,
所以x+5x=180°,
解得x=30°,
即∠BOC=30°.
因为OE是∠BOC的平分线,
所以∠BOE=∠COE=15°.
11.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:(1)因为OA平分∠EOC,
所以∠AOC=∠EOC=×70°=35°.
所以∠BOD=∠AOC=35°.
(2)设∠EOC=2x,则∠EOD=3x.根据题意,得2x+3x=180°.解得x=36°.
则∠EOC=2x=72°.
所以∠AOC=∠EOC=×72°=36°.
所以∠BOD=∠AOC=36°.
C组
12.(2022春·香坊区期末)如图,直线AB,CD相交于点O,
∠BOM=∠DON=90°.
(1)如图1,若∠COM=35°,求∠BON的度数;
(2)如图1,请直接写出图中所有互余的角;
(3)如图2,若射线OE在∠MOB的内部,且∠MON-∠BOE=45°,请比较∠MOE与∠DOE的大小并说明理由.
解:(1)因为BOM=90°,
所以∠AOM=90°.
因为∠COM=35°,
所以∠AOC=55°,
所以∠BOD=55°.
因为∠DON=90°,
所以∠BON=∠BOD+∠DON=55°+90°=145°.
(2)因为∠AOC+∠COM=90°,
所以∠AOC与∠COM互余.
因为∠AOC+∠AON=90°,
所以∠AOC与∠AON互余.
因为∠BOD=∠AOC,
所以∠BOD与∠COM互余,∠BOD与∠AON互余.
(3)∠MOE=∠DOE.
因为∠BOM=∠DON=90°,
所以∠MOC=∠AON.
设∠MOC=x,则∠AON=x,∠AOC=∠BOD=90°-x.
因为∠MON-∠BOE=45°,
所以(90°+x)-∠BOE=45°,
所以∠BOE=x,
所以∠MOE=90°-x,
∠DOE=∠BOD+∠BOE=90°-x+x=90°-x,
所以∠MOE=∠DOE.
03
课标要求
01
基础梳理
02
典例探究
课时训练
04
第五章 相交线与平行线
5.1 相交线
第1课时 相交线
课标要求
理解对顶角、邻补角等概念,探索并掌握对顶角相等、邻补角互补的性质.
基础梳理
1.邻补角:
(1)概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为 . 图中还有其他的邻补角:_________________
.
邻补角
∠1和∠4,∠3和∠4,
∠3和∠2
(2)性质:邻补角 .
互补
2.对顶角:
(1)概念:如上图,∠1和∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为 .图中还有其他的对顶角: .
(2)性质:对顶角 .
对顶角
∠2和∠4
相等
基础过关
1.(2023春·荣昌区期末)下列各图中,∠1与∠2是邻补角的是( )
A B C D
D
2.下列各图中,∠1和∠2是对顶角吗
不是
是
不是
不是
是
典例探究
知识点1 邻补角、对顶角的定义
【例题1】如图,直线AB,CD相交于点O,OE为以点O为端点的射线,写出图中所有的邻补角和对顶角.
解:互为邻补角的有∠AOE和∠BOE,∠AOD和∠BOD,∠AOC和∠BOC,∠AOC和∠AOD,∠COE和∠DOE,∠BOC和∠BOD.
互为对顶角的有∠AOD和∠BOC,∠AOC和∠BOD.
【变式1】如图,直线AB,CD,EF相交于点O,共有 组对顶角:
(1)∠AOC的对顶角是 ;
(2)∠AOD的对顶角是 ;
(3)∠BOC的邻补角是 .
6
∠BOD
∠BOC
∠AOC,∠BOD
知识点2 邻补角、对顶角的性质
【例题2】(2022春·泾阳县期中)如图所示,直线a,b,c两两相交,∠1=∠3+12°,∠2=52°,求∠4的度数.
解:因为∠1与∠2是对顶角,
所以∠1=∠2=52°.
因为∠1=∠3+12°=52°,
所以∠3=40°.
因为∠3与∠4是邻补角,
所以∠4=180°-∠3=180°-40°=140°.
【变式2】如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
解:(1)因为∠1与∠2互为邻补角,
所以∠2=180°-∠1.
因为∠1=50°,
所以∠2=180°-50°=130°.
(2)因为∠1与∠2互为邻补角,
所以∠2+∠1=180°.
因为∠2=3∠1,
所以3∠1+∠1=180°.
解得∠1=45°.
那么∠2=3×45°=135°.
所以∠3=∠1=45°,∠4=∠2=135°.
课时训练
A组
1.(2023春·榆次区期中)如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型.固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是 ( )
A.∠2增大4° B.∠3增大4°
C.∠4增大4° D.∠4减小2°
B
2.如图,直线AB,CD相交于点O,OE,OF为过点O的射线,则对顶角有 ( )
A.1对
B.2对
C.3对
D.4对
B
3.∠1与∠2是对顶角,∠2与∠3是邻补角.若∠1=35°,则∠3的大小是 ( )
A.35° B.55° C.125° D.145°
D
4.(2022春·夏邑县期中)如图,直线AB与CD相交于点O,
∠AOC-2∠AOE=20°,射线OF平分∠DOE,若∠BOD=60°,则∠AOF的度数为 ( )
A.50° B.60°
C.70° D.80°
第4题图
C
5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于 ( )
A.38° B.104°
C.142° D.144°
第5题图
C
6.如图,三条直线AB,CD,EF两两相交,在这个图形中,有对顶角 对,邻补角 对.
第6题图
6
12
7.如图,直线AB,CD,EF相交于点O,则∠AOD的对顶角是∠BOC,∠AOC的邻补角是 , ;若∠AOC=50°,则∠BOD= ,∠COB= .
第7题图
∠AOD
∠BOC
50°
130°
8.(2022春·胶州市期中)如图,两条直线相交于点O,若∠1+∠2=68°,则∠1= .
34°
9.如图,直线AB,CD,EF相交于点O.
(1)请写出∠AOC,∠AOE,∠EOC的对顶角;
(2)若∠AOC=50°,求∠BOD,∠BOC的度数.
解:(1)∠AOC的对顶角是∠BOD,∠AOE的对顶角是∠BOF,∠EOC的对顶角是∠DOF.
(2)因为∠AOC=50°,
所以∠BOD=50°,∠BOC=180°-50°=130°.
B组
10.(2022春·关岭县期末)如图,直线AB,CD相交于点O,OE是∠BOC的平分线,若∠BOC∶∠AOC=1∶5.求∠BOE的度数.
解:因为∠BOC∶∠AOC=1∶5,
设∠BOC=x,则∠AOC=5x,
因为∠BOC+∠AOC=180°,
所以x+5x=180°,
解得x=30°,
即∠BOC=30°.
因为OE是∠BOC的平分线,
所以∠BOE=∠COE=15°.
11.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:(1)因为OA平分∠EOC,
所以∠AOC=∠EOC=×70°=35°.
所以∠BOD=∠AOC=35°.
(2)设∠EOC=2x,则∠EOD=3x.根据题意,得2x+3x=180°.解得x=36°.
则∠EOC=2x=72°.
所以∠AOC=∠EOC=×72°=36°.
所以∠BOD=∠AOC=36°.
C组
12.(2022春·香坊区期末)如图,直线AB,CD相交于点O,
∠BOM=∠DON=90°.
(1)如图1,若∠COM=35°,求∠BON的度数;
(2)如图1,请直接写出图中所有互余的角;
(3)如图2,若射线OE在∠MOB的内部,且∠MON-∠BOE=45°,请比较∠MOE与∠DOE的大小并说明理由.
解:(1)因为BOM=90°,
所以∠AOM=90°.
因为∠COM=35°,
所以∠AOC=55°,
所以∠BOD=55°.
因为∠DON=90°,
所以∠BON=∠BOD+∠DON=55°+90°=145°.
(2)因为∠AOC+∠COM=90°,
所以∠AOC与∠COM互余.
因为∠AOC+∠AON=90°,
所以∠AOC与∠AON互余.
因为∠BOD=∠AOC,
所以∠BOD与∠COM互余,∠BOD与∠AON互余.
(3)∠MOE=∠DOE.
因为∠BOM=∠DON=90°,
所以∠MOC=∠AON.
设∠MOC=x,则∠AON=x,∠AOC=∠BOD=90°-x.
因为∠MON-∠BOE=45°,
所以(90°+x)-∠BOE=45°,
所以∠BOE=x,
所以∠MOE=90°-x,
∠DOE=∠BOD+∠BOE=90°-x+x=90°-x,
所以∠MOE=∠DOE.
