六年级数学下册人教版3.3 整理和复习(课件)(共29张PPT)
文档属性
| 名称 | 六年级数学下册人教版3.3 整理和复习(课件)(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:33:43 | ||
图片预览







文档简介
(共29张PPT)
第三单元 圆柱与圆锥
第11课时 整理和复习
圆柱与圆锥
圆柱
圆锥
圆
柱
的
认
识
表
面
积
体
积
圆
锥
的
认
识
体
积
底
上底=下底
高
圆
柱
曲面
圆柱有无数条高
1个侧面
2个底面
圆
圆柱可看成长(正)方形旋转一周形成的。
1.圆柱的形成
侧面
底面
底面
侧面
长方形的宽=圆柱的高
长方形的长=圆柱底面周长
2.圆柱的展开图
侧面沿高展开后是一个长方形或正方形。
底面
底面
侧面
长
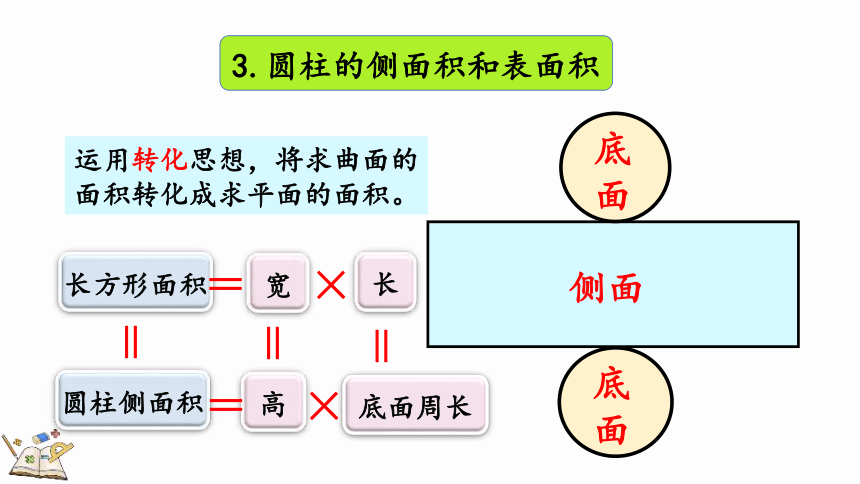
圆柱侧面积
长方形面积
宽
高
底面周长
=
=
=
=
×
=
×
3.圆柱的侧面积和表面积
运用转化思想,将求曲面的面积转化成求平面的面积。
圆柱表面积=侧面积+2个底面积
底面
底面
侧面
h
r
S表=S侧+2×πr2
=2πrh+2πr2
高
底面周长
2πr
圆柱侧面积
S侧
= ×
3.圆柱的侧面积和表面积
= ×
在解决实际问题时,并不是所有圆柱都有两个底面,有的有一个,有的没有,要具体问题具体分析。
4.圆柱的体积
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
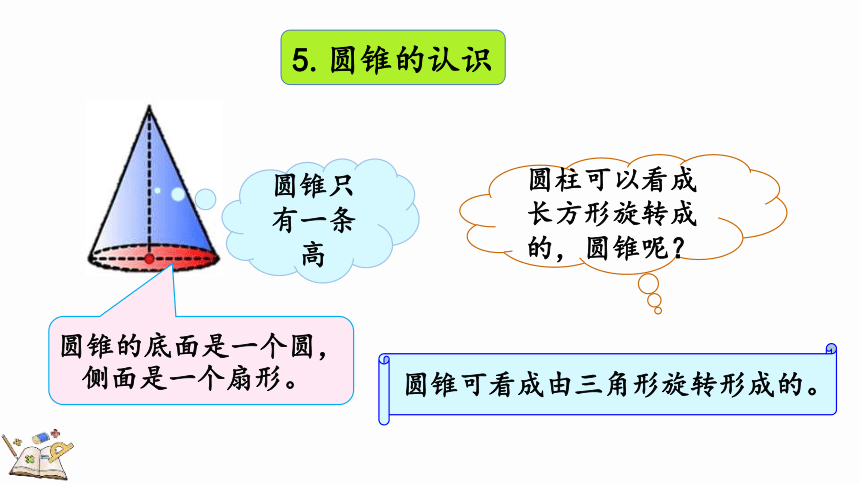
圆柱可以看成长方形旋转成的,圆锥呢?
圆锥的底面是一个圆,侧面是一个扇形。
圆锥只有一条高
圆锥可看成由三角形旋转形成的。
5.圆锥的认识
圆锥的体积是与它等底等高的圆柱体积的。
V圆锥=×πr2×h
底面积×高
圆锥体积=×底面积×高
6.圆锥的体积
切割问题:切割前后的表面积增加了,体积不变。
7.解决问题
新增两个一组邻边分别为圆柱的底面直径和高的长方形或正方形。
新增两个与底面完全相同的圆。
等积变形:只是形状发生了变化,体积不变。
7.解决问题
转
化
法
利用物体体积不变的特征,可以把不规则物体的体积转化成规则物体的体积来计算。
选自教材第36页整理和复习第1~4题
1
将下面的图形分类,说一说每类图形的名称和特征。
圆柱
圆锥
1
将下面的图形分类,说一说每类图形的名称和特征。
底面
侧面
O
O
高
底面
圆柱的上、下两个面叫做底面。是圆形。
圆柱周围的面(上、下底面除外)叫做侧
面。一般来说圆柱的侧面展开图是(长
方形或正方形)。
圆柱的两个底面之间的距离叫做高。
圆柱有无数条相等的高。
1
将下面的图形分类,说一说每类图形的名称和特征。
圆锥是由2个面组成的。
圆锥的下面叫做底面。
圆锥周围的面(底面除外)叫做侧面。
圆锥的侧面展开图是扇形。
从圆锥的顶点到底面圆心的距离是圆
锥的高。圆锥只有1条高。
底面
顶点
O
r
高
h
2
想一想:怎样计算圆柱的侧面积、表面积?圆柱、圆锥的
体积计算公式是怎样推导出来的?再填写下表。
名称 底面半径 底面直径 高 表面积 体积
圆柱 5 dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 6 dm ——
0.5m 12 m ——
2
圆柱的侧面积=底面周长×高
展开
侧面
底面的周长
高
底面的周长
侧面
侧面
直接计算:S侧=Ch
利用直径计算:S侧=πdh
利用半径计算:S侧=2πrh
圆柱的侧面积
2
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
利用直径计算:S表=πdh+2π(d÷2)2
利用半径计算:S表=2πrh+ 2πr2
利用周长计算:S表=Ch+2π(C÷2π)2
圆柱的表面积
2
圆柱的体积
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
2
圆锥的体积
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
圆锥的体积=圆锥的底面积×高×
2
圆柱和圆锥的特征与关系
圆柱 圆锥
底面
侧面
高
表面积
体积
关系
两个,圆形。完全相同,互相平行。
一个,圆形。
无数条,一样长。
一个,曲面,展开后是扇形。
一条。
S表=2S底+S侧
V=Sh
一个,曲面,展开后是长方形或正
方形或平行四边形。
V = Sh
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
2
图形 底面半径 底面直径 高 表面积 体积
圆柱 5 dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 6 dm ——
0.5m 12 m ——
10dm
282.6dm2
314dm3
1m
10.676m2
2.198m3
40cm
3140cm2
6280cm3
2dm
25.12 dm3
1m
3.14 m3
填写下表。
3
(1)做这个布套至少用了多少布料?
小雨的水壶有一个布套(如右图)。
至少用的布料=圆柱的表面积
3.14×10×20+3.14× (10÷2)2×2
=628+157
=785(cm2)
答:做这个布套至少用了785 cm2布料。
3
(2)这个水壶能装下1.6 L水吗?(水壶和布套的厚度忽略不计。)
小雨的水壶有一个布套(如右图)。
一壶水的体积=壶的容积
3.14×(10÷2)2×20=1570(cm3)
1570 cm3=1.57 L
1.57<1.6
答:这个水壶不能装下1.6 L水。
4
一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4dm,圆柱高2dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
3.14×(4÷2)2×2 + 3.14×(4÷2)2×4.2÷3
=42.704(dm3)
42.704×0.65≈28(kg)
答:这个进料漏斗大约能装28 kg稻谷。
4
一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4dm,圆柱高2dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
大米的质量=稻谷的质量×出米率
28×70%=19.6(kg)
答:一漏斗稻谷大约能磨出19.6 kg大米。
1.
李大伯家挖了一个圆形鱼塘,如下图,要在鱼塘四周和底部抹水泥。需要抹水泥的面积是多大?
1.5m
40m
只有一个底面
抹水泥面积:1256+188.4=1444.4(m2)
答:需要抹水泥的面积是1444.4 m2。
半径:
40÷2=20(m)
底面积πr2
=20×20×π
=1256(m2)
侧面积2πr×h
=2π×20×1.5
=188.4(m2)
2.
如图,一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少?
上面是圆锥
下面是圆柱
圆锥的体积
圆柱的体积
+
3.14×42×(8-5)÷3
3.14×42×5
=301.44(cm3)
答:旋转一周后形成的立体图形的体积是301.44cm3。
=50.24 + 251.2
+
3.
×π( )2×
蚁狮用来捕食的洞穴是个倒圆锥形。蚁狮挖了一个洞口直径约4.2厘米、深2厘米的倒圆锥形洞穴,大约需要挖多少土
圆锥的体积
= × πr2 × h
4.2÷2
2
= 9.2316(cm3)
答:大约需要挖9.2316 cm3土。
求体积
圆柱的认识
圆柱的体积:
圆柱的表面积
圆锥的认识
圆柱与圆锥
侧面积:
各部分名称
圆锥的体积:
特征:
有无数条高
表面积:
S侧=Ch=πdh=2πrh
S表=S侧+2S底2πrh+ 2πr2
V=Sh=πr2h
各部分名称
有1条高
特征:
V=Sh=πr2h
底面
顶点
O
r
高
第三单元 圆柱与圆锥
第11课时 整理和复习
圆柱与圆锥
圆柱
圆锥
圆
柱
的
认
识
表
面
积
体
积
圆
锥
的
认
识
体
积
底
上底=下底
高
圆
柱
曲面
圆柱有无数条高
1个侧面
2个底面
圆
圆柱可看成长(正)方形旋转一周形成的。
1.圆柱的形成
侧面
底面
底面
侧面
长方形的宽=圆柱的高
长方形的长=圆柱底面周长
2.圆柱的展开图
侧面沿高展开后是一个长方形或正方形。
底面
底面
侧面
长
圆柱侧面积
长方形面积
宽
高
底面周长
=
=
=
=
×
=
×
3.圆柱的侧面积和表面积
运用转化思想,将求曲面的面积转化成求平面的面积。
圆柱表面积=侧面积+2个底面积
底面
底面
侧面
h
r
S表=S侧+2×πr2
=2πrh+2πr2
高
底面周长
2πr
圆柱侧面积
S侧
= ×
3.圆柱的侧面积和表面积
= ×
在解决实际问题时,并不是所有圆柱都有两个底面,有的有一个,有的没有,要具体问题具体分析。
4.圆柱的体积
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
圆柱可以看成长方形旋转成的,圆锥呢?
圆锥的底面是一个圆,侧面是一个扇形。
圆锥只有一条高
圆锥可看成由三角形旋转形成的。
5.圆锥的认识
圆锥的体积是与它等底等高的圆柱体积的。
V圆锥=×πr2×h
底面积×高
圆锥体积=×底面积×高
6.圆锥的体积
切割问题:切割前后的表面积增加了,体积不变。
7.解决问题
新增两个一组邻边分别为圆柱的底面直径和高的长方形或正方形。
新增两个与底面完全相同的圆。
等积变形:只是形状发生了变化,体积不变。
7.解决问题
转
化
法
利用物体体积不变的特征,可以把不规则物体的体积转化成规则物体的体积来计算。
选自教材第36页整理和复习第1~4题
1
将下面的图形分类,说一说每类图形的名称和特征。
圆柱
圆锥
1
将下面的图形分类,说一说每类图形的名称和特征。
底面
侧面
O
O
高
底面
圆柱的上、下两个面叫做底面。是圆形。
圆柱周围的面(上、下底面除外)叫做侧
面。一般来说圆柱的侧面展开图是(长
方形或正方形)。
圆柱的两个底面之间的距离叫做高。
圆柱有无数条相等的高。
1
将下面的图形分类,说一说每类图形的名称和特征。
圆锥是由2个面组成的。
圆锥的下面叫做底面。
圆锥周围的面(底面除外)叫做侧面。
圆锥的侧面展开图是扇形。
从圆锥的顶点到底面圆心的距离是圆
锥的高。圆锥只有1条高。
底面
顶点
O
r
高
h
2
想一想:怎样计算圆柱的侧面积、表面积?圆柱、圆锥的
体积计算公式是怎样推导出来的?再填写下表。
名称 底面半径 底面直径 高 表面积 体积
圆柱 5 dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 6 dm ——
0.5m 12 m ——
2
圆柱的侧面积=底面周长×高
展开
侧面
底面的周长
高
底面的周长
侧面
侧面
直接计算:S侧=Ch
利用直径计算:S侧=πdh
利用半径计算:S侧=2πrh
圆柱的侧面积
2
底面
底面
侧面
底面的周长
高
圆柱的表面积=圆柱侧面积+底面积×2
直接计算:S表=S侧+2S底
利用直径计算:S表=πdh+2π(d÷2)2
利用半径计算:S表=2πrh+ 2πr2
利用周长计算:S表=Ch+2π(C÷2π)2
圆柱的表面积
2
圆柱的体积
圆柱的体积=圆柱的底面积×高
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
2
圆锥的体积
直接计算:V=Sh
利用直径计算:V=π(d÷2)2h
利用半径计算:V=πr2h
利用周长计算:V=π(C÷2π)2h
圆锥的体积=圆锥的底面积×高×
2
圆柱和圆锥的特征与关系
圆柱 圆锥
底面
侧面
高
表面积
体积
关系
两个,圆形。完全相同,互相平行。
一个,圆形。
无数条,一样长。
一个,曲面,展开后是扇形。
一条。
S表=2S底+S侧
V=Sh
一个,曲面,展开后是长方形或正
方形或平行四边形。
V = Sh
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
2
图形 底面半径 底面直径 高 表面积 体积
圆柱 5 dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 6 dm ——
0.5m 12 m ——
10dm
282.6dm2
314dm3
1m
10.676m2
2.198m3
40cm
3140cm2
6280cm3
2dm
25.12 dm3
1m
3.14 m3
填写下表。
3
(1)做这个布套至少用了多少布料?
小雨的水壶有一个布套(如右图)。
至少用的布料=圆柱的表面积
3.14×10×20+3.14× (10÷2)2×2
=628+157
=785(cm2)
答:做这个布套至少用了785 cm2布料。
3
(2)这个水壶能装下1.6 L水吗?(水壶和布套的厚度忽略不计。)
小雨的水壶有一个布套(如右图)。
一壶水的体积=壶的容积
3.14×(10÷2)2×20=1570(cm3)
1570 cm3=1.57 L
1.57<1.6
答:这个水壶不能装下1.6 L水。
4
一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4dm,圆柱高2dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
3.14×(4÷2)2×2 + 3.14×(4÷2)2×4.2÷3
=42.704(dm3)
42.704×0.65≈28(kg)
答:这个进料漏斗大约能装28 kg稻谷。
4
一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4dm,圆柱高2dm,圆锥高4.2 dm。每立方分米稻谷大约重0.65 kg。
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
大米的质量=稻谷的质量×出米率
28×70%=19.6(kg)
答:一漏斗稻谷大约能磨出19.6 kg大米。
1.
李大伯家挖了一个圆形鱼塘,如下图,要在鱼塘四周和底部抹水泥。需要抹水泥的面积是多大?
1.5m
40m
只有一个底面
抹水泥面积:1256+188.4=1444.4(m2)
答:需要抹水泥的面积是1444.4 m2。
半径:
40÷2=20(m)
底面积πr2
=20×20×π
=1256(m2)
侧面积2πr×h
=2π×20×1.5
=188.4(m2)
2.
如图,一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少?
上面是圆锥
下面是圆柱
圆锥的体积
圆柱的体积
+
3.14×42×(8-5)÷3
3.14×42×5
=301.44(cm3)
答:旋转一周后形成的立体图形的体积是301.44cm3。
=50.24 + 251.2
+
3.
×π( )2×
蚁狮用来捕食的洞穴是个倒圆锥形。蚁狮挖了一个洞口直径约4.2厘米、深2厘米的倒圆锥形洞穴,大约需要挖多少土
圆锥的体积
= × πr2 × h
4.2÷2
2
= 9.2316(cm3)
答:大约需要挖9.2316 cm3土。
求体积
圆柱的认识
圆柱的体积:
圆柱的表面积
圆锥的认识
圆柱与圆锥
侧面积:
各部分名称
圆锥的体积:
特征:
有无数条高
表面积:
S侧=Ch=πdh=2πrh
S表=S侧+2S底2πrh+ 2πr2
V=Sh=πr2h
各部分名称
有1条高
特征:
V=Sh=πr2h
底面
顶点
O
r
高
