六年级数学下册人教版3.2.3 练习六课件(共25张PPT)
文档属性
| 名称 | 六年级数学下册人教版3.2.3 练习六课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 19:34:30 | ||
图片预览






文档简介
(共25张PPT)
练习六
第三单元 圆柱与圆锥
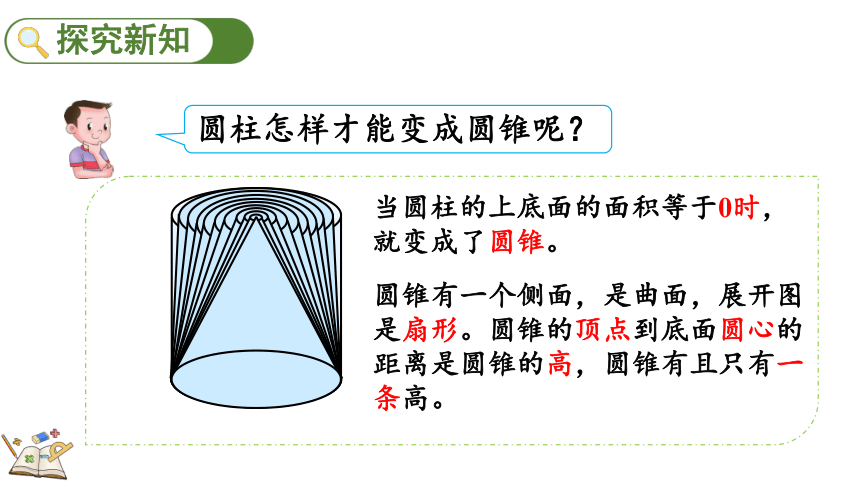
圆柱怎样才能变成圆锥呢?
当圆柱的上底面的面积等于0时,就变成了圆锥。
圆锥有一个侧面,是曲面,展开图是扇形。圆锥的顶点到底面圆心的距离是圆锥的高,圆锥有且只有一条高。
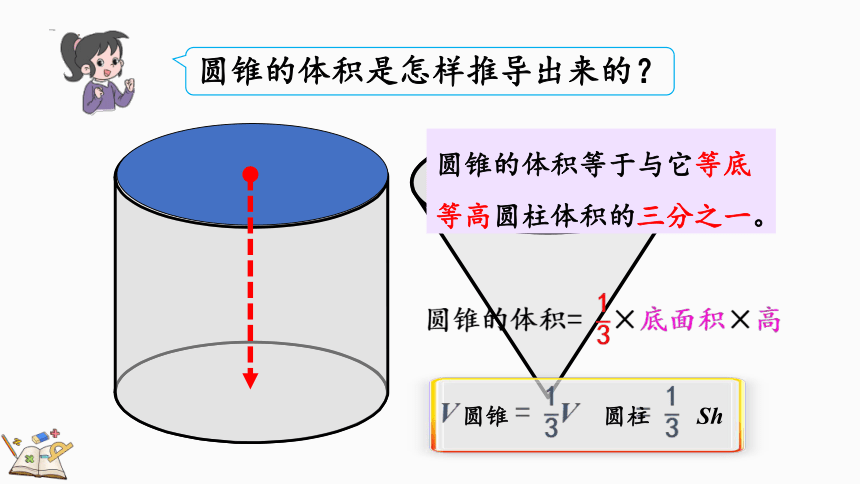
圆锥的体积是怎样推导出来的?
圆锥的体积等于与它等底等高圆柱体积的三分之一。
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
圆锥的体积= ×底面积×高
怎样求圆锥的体积?
V= Sh
V= πr2h
V= π(d÷2)2h
V= π(C÷2π)2h
已知底面积和高:
已知底面半径和高:
已知底面直径和高:
已知底面周长和高:
选自教材第34~35页练习六
1
下列物体的形状是由哪些图形组成的?
圆柱和圆锥
圆柱
圆柱和圆锥
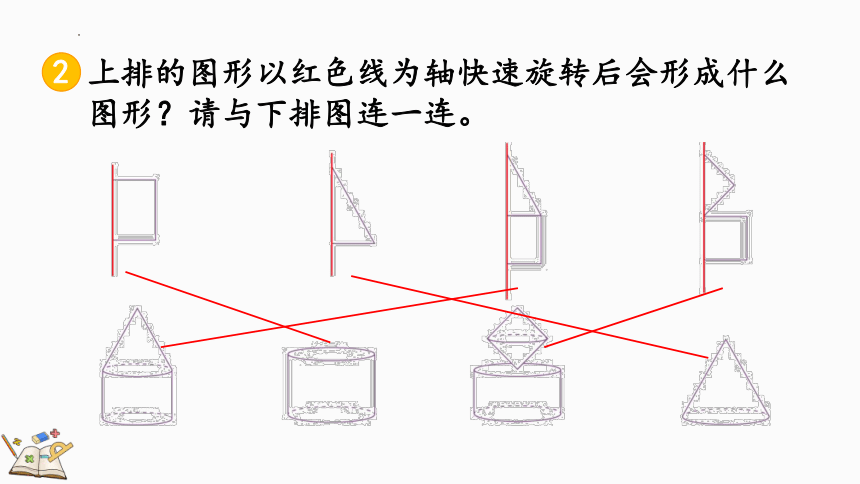
2
上排的图形以红色线为轴快速旋转后会形成什么图形?请与下排图连一连。
3
圆锥的体积是与它等底等高的圆柱体积的三分之一。
一个圆柱的体积是75.36 m3,与它等底、
等高的圆锥的体积是( )m3。
(1)
一个圆锥的体积是141.3 m3,与它等底、等高的圆柱的体积是( )m3。
(2)
25.12
423.9
4
圆锥的体积等于等底、等高的圆柱体积的三分之一。
判断下面的说法是否正确,并说一说你的理由。
(1)
圆锥的体积等于圆柱体积的 。
错误
(2)
圆柱的体积大于与它等底、等高的圆锥的体积。
(3)
圆锥的高是圆柱的高的3倍,它们的体积一定相等。
正确
错误
理由:只有底面积相等时才正确。
5
一个圆锥的底面周长是31.4 cm,高是9 cm 。它的体积是多少?
答:它的体积是235.5cm3。
V= π(C÷2 π )2h
3
1
×3.14×(31.4÷3.14÷2)2×9 = 235.5(cm3)
1
3
6
一堆煤呈圆锥形,高为2m,底面周长为18.84m。这堆煤的体积是多少?
×3.14×(18.84÷3.14÷2)2×2 =18.84(m3)
3
1
18.84×1.4≈26(吨)
答:这堆煤的体积是18.84m3。这堆煤大约重26吨。
已知每立方米的煤大约重1.4 t,这堆煤大约重多少吨?(得数保留整数。)
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(1)
这堆稻谷的体积大约是多少?
答:这堆稻谷的体积大约是6.28m3。
×3.14×(4÷2)2×1.5=6.28(m )
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(2)如果每立方米稻谷大约重650 kg,这堆稻谷大约重多少千克?
650×6.28=4082(kg)
答:这堆稻谷大约重4082kg。
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(3)
小明家有0.4公顷稻田,平均每公顷大约产稻谷多少千克?
4082÷0.4=10205 (kg)
答:平均每公顷大约产稻谷10205 kg。
(4)
如果每千克稻谷售价为2.8元,这些稻谷大约能卖多少钱?
4082×2.8=11429.6(元)
答:这些稻谷大约能卖11429.6元。
8
当圆锥与它底面积相等的圆柱的体积也相等,那么圆锥的高就是圆柱的高的3倍。
一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
9
一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26cm2,圆柱的底面积是多少?
28.26÷3=9.42 (cm2)
答:圆柱的底面积是9.42cm2。
10
用底面半径和高分别是6 cm、12 cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如右图)。在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2 cm。若将这个容器上面封住并倒立,细沙的高度是多少厘米?
圆柱与圆锥等底、等高
12÷3
+2=6(厘米)
答:细沙的高度是6厘米。
11
*
一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200km2,某日平均降水量为50mm,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
根据土地面积和降水的高求出降水的体积,再求出它的25%是多少,最后与200比较大小。
11
*
200km =200000000m =20000万平方米
50mm=0.05m
0.05×20000=1000(万立方米)
1000×25%=250(万立方米)
250>200
答:该日该地区总降水为1000万立方米。
这些雨水的25%能满足绿化所需。
1.
(1)一个圆柱的体积是75.36m ,与它等底、等高的圆锥的体积
是( )m 。
(2)一个圆锥的体积是141.3m ,与它等底、等高的圆柱的体积
是( )m 。
141.3×3=423.9(m )
75.36×=25.12(m )
填一填。
423.9
25.12
Ⅴ = V
锥
3
柱
Ⅴ =V
锥
柱
2.
将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
表面积增加两个长方形,长等于圆柱的高,宽等于圆柱底面直径。
h: 40÷2÷4=5(厘米)
3.14×(4÷2)2×5
=3.14×4×5
=62.8(cm 3 )
答:这个圆柱的体积是62.8cm 3。
3.
一个圆锥与一个圆柱等底、等高,已知它们的体积之和是48立方分米,那么圆锥的体积是多少立方分米?圆柱呢?
圆柱的体积:12×3=36(立方分米)
答:圆锥的体积是12立方分米,圆柱的体积是36立方分米。
V = 3V
柱
锥
圆锥的体积:48÷(1+3)=12(立方分米)
4.
明明把一块底面周长是18.84cm,高5cm的圆柱体橡皮泥捏成一个底面直径是8cm的圆锥体,这个圆锥体的高是多少厘米?(得数保留一位小数)
≈8.4(cm)
18.84÷3.14÷2=3(cm)
答:这个圆锥体的高是8.4cm。
3×3.14×32×5÷[3.14×(8÷2)2
[
圆柱体变成圆锥体,形状变了,前后体积没变。
=423.9÷50.24
5.
一个圆柱形鱼缸,底面直径是60cm,高是30cm,里面盛了一些水,把一个底面半径为20cm的圆锥放入鱼缸中(圆锥全部浸入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
2cm
答:这个圆锥的高是13.5cm。
鱼缸中水面升高的那部分圆柱的体积就是放入水中的圆锥的体积。
=3.14×(60÷2)2×2
=3.14×1800
=5652(cm3)
V =
锥
柱
V
V = Sh
锥
h =3V ÷S
锥
=3×5652÷(3.14×202)
=16956÷1256
=13.5(cm)
这节课有什么收获呢?
速记宝典
圆锥体积容易算,它与圆柱有关联。
等底等高不能忘,三分之一记心间。
题中条件亮红灯,单位一致需看清。
计算一定要仔细,这样才能出成绩。
组成
体积:
圆锥的认识与体积
底面:圆
侧面:曲面
V= Sh
练习六
第三单元 圆柱与圆锥
圆柱怎样才能变成圆锥呢?
当圆柱的上底面的面积等于0时,就变成了圆锥。
圆锥有一个侧面,是曲面,展开图是扇形。圆锥的顶点到底面圆心的距离是圆锥的高,圆锥有且只有一条高。
圆锥的体积是怎样推导出来的?
圆锥的体积等于与它等底等高圆柱体积的三分之一。
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
圆锥的体积= ×底面积×高
怎样求圆锥的体积?
V= Sh
V= πr2h
V= π(d÷2)2h
V= π(C÷2π)2h
已知底面积和高:
已知底面半径和高:
已知底面直径和高:
已知底面周长和高:
选自教材第34~35页练习六
1
下列物体的形状是由哪些图形组成的?
圆柱和圆锥
圆柱
圆柱和圆锥
2
上排的图形以红色线为轴快速旋转后会形成什么图形?请与下排图连一连。
3
圆锥的体积是与它等底等高的圆柱体积的三分之一。
一个圆柱的体积是75.36 m3,与它等底、
等高的圆锥的体积是( )m3。
(1)
一个圆锥的体积是141.3 m3,与它等底、等高的圆柱的体积是( )m3。
(2)
25.12
423.9
4
圆锥的体积等于等底、等高的圆柱体积的三分之一。
判断下面的说法是否正确,并说一说你的理由。
(1)
圆锥的体积等于圆柱体积的 。
错误
(2)
圆柱的体积大于与它等底、等高的圆锥的体积。
(3)
圆锥的高是圆柱的高的3倍,它们的体积一定相等。
正确
错误
理由:只有底面积相等时才正确。
5
一个圆锥的底面周长是31.4 cm,高是9 cm 。它的体积是多少?
答:它的体积是235.5cm3。
V= π(C÷2 π )2h
3
1
×3.14×(31.4÷3.14÷2)2×9 = 235.5(cm3)
1
3
6
一堆煤呈圆锥形,高为2m,底面周长为18.84m。这堆煤的体积是多少?
×3.14×(18.84÷3.14÷2)2×2 =18.84(m3)
3
1
18.84×1.4≈26(吨)
答:这堆煤的体积是18.84m3。这堆煤大约重26吨。
已知每立方米的煤大约重1.4 t,这堆煤大约重多少吨?(得数保留整数。)
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(1)
这堆稻谷的体积大约是多少?
答:这堆稻谷的体积大约是6.28m3。
×3.14×(4÷2)2×1.5=6.28(m )
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(2)如果每立方米稻谷大约重650 kg,这堆稻谷大约重多少千克?
650×6.28=4082(kg)
答:这堆稻谷大约重4082kg。
7
小明家收获的稻谷堆成了圆锥形,高约为1.5m,底面直径约为4m。
(3)
小明家有0.4公顷稻田,平均每公顷大约产稻谷多少千克?
4082÷0.4=10205 (kg)
答:平均每公顷大约产稻谷10205 kg。
(4)
如果每千克稻谷售价为2.8元,这些稻谷大约能卖多少钱?
4082×2.8=11429.6(元)
答:这些稻谷大约能卖11429.6元。
8
当圆锥与它底面积相等的圆柱的体积也相等,那么圆锥的高就是圆柱的高的3倍。
一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
9
一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26cm2,圆柱的底面积是多少?
28.26÷3=9.42 (cm2)
答:圆柱的底面积是9.42cm2。
10
用底面半径和高分别是6 cm、12 cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如右图)。在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高2 cm。若将这个容器上面封住并倒立,细沙的高度是多少厘米?
圆柱与圆锥等底、等高
12÷3
+2=6(厘米)
答:细沙的高度是6厘米。
11
*
一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。某地区的土地面积为200km2,某日平均降水量为50mm,该日该地区总降水为多少万立方米?该地区一年绿化用水为200万立方米,这些雨水的25%能满足绿化所需吗?
根据土地面积和降水的高求出降水的体积,再求出它的25%是多少,最后与200比较大小。
11
*
200km =200000000m =20000万平方米
50mm=0.05m
0.05×20000=1000(万立方米)
1000×25%=250(万立方米)
250>200
答:该日该地区总降水为1000万立方米。
这些雨水的25%能满足绿化所需。
1.
(1)一个圆柱的体积是75.36m ,与它等底、等高的圆锥的体积
是( )m 。
(2)一个圆锥的体积是141.3m ,与它等底、等高的圆柱的体积
是( )m 。
141.3×3=423.9(m )
75.36×=25.12(m )
填一填。
423.9
25.12
Ⅴ = V
锥
3
柱
Ⅴ =V
锥
柱
2.
将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
表面积增加两个长方形,长等于圆柱的高,宽等于圆柱底面直径。
h: 40÷2÷4=5(厘米)
3.14×(4÷2)2×5
=3.14×4×5
=62.8(cm 3 )
答:这个圆柱的体积是62.8cm 3。
3.
一个圆锥与一个圆柱等底、等高,已知它们的体积之和是48立方分米,那么圆锥的体积是多少立方分米?圆柱呢?
圆柱的体积:12×3=36(立方分米)
答:圆锥的体积是12立方分米,圆柱的体积是36立方分米。
V = 3V
柱
锥
圆锥的体积:48÷(1+3)=12(立方分米)
4.
明明把一块底面周长是18.84cm,高5cm的圆柱体橡皮泥捏成一个底面直径是8cm的圆锥体,这个圆锥体的高是多少厘米?(得数保留一位小数)
≈8.4(cm)
18.84÷3.14÷2=3(cm)
答:这个圆锥体的高是8.4cm。
3×3.14×32×5÷[3.14×(8÷2)2
[
圆柱体变成圆锥体,形状变了,前后体积没变。
=423.9÷50.24
5.
一个圆柱形鱼缸,底面直径是60cm,高是30cm,里面盛了一些水,把一个底面半径为20cm的圆锥放入鱼缸中(圆锥全部浸入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
2cm
答:这个圆锥的高是13.5cm。
鱼缸中水面升高的那部分圆柱的体积就是放入水中的圆锥的体积。
=3.14×(60÷2)2×2
=3.14×1800
=5652(cm3)
V =
锥
柱
V
V = Sh
锥
h =3V ÷S
锥
=3×5652÷(3.14×202)
=16956÷1256
=13.5(cm)
这节课有什么收获呢?
速记宝典
圆锥体积容易算,它与圆柱有关联。
等底等高不能忘,三分之一记心间。
题中条件亮红灯,单位一致需看清。
计算一定要仔细,这样才能出成绩。
组成
体积:
圆锥的认识与体积
底面:圆
侧面:曲面
V= Sh
