【2024春人教七下数学精品教案】5_1_1 相交线
文档属性
| 名称 | 【2024春人教七下数学精品教案】5_1_1 相交线 |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 23:47:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1.1 相交线 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线”5.1.1相交线,内容包括:邻补角与对顶角的概念及性质.
2.内容解析
本节课是在学习了直线、射线、线段和角的有关知识的基础上,进一步研究平面内两条直线相交形成4个角的位置和数量关系,为今后学习几何奠定了基础,同时也为证明几何题提供了一个示范作用,本节对于进一步培养学生的识图能力,激发学生的学习兴趣具有推动作用,所以本节课具有很重要的地位和作用。
基于以上分析,确定本节课的教学重点为:掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
二、目标和目标解析
1.目标
(1)理解两条直线相交的特征及邻补角与对顶角的概念.
(2)掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
2.目标解析
理解对顶角和邻补角的概念,能从图中辨别对顶角和邻补角。掌握“对顶角相等的性质”,理解对顶角相等的说理过程,在数学活动中培养学生的观察、转化、说理能力和语言规范表达能力。通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣;在解题中感受生活中数学的存在,体验数学中充满着探索和创造。
三、教学问题诊断分析
七年级的孩子思维活跃,模仿能力强。同时他们也具备了一定的学习能力,在老师的指导下,能针对某一问题展开讨论并归纳总结。但是受年龄特征的影响,他们对知识迁移能力不强,推理能力还需进一步培养。
基于以上学情分析,掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
四、教学过程设计
情境引入
你能在身边找出一些相交线的实例吗?
自学导航
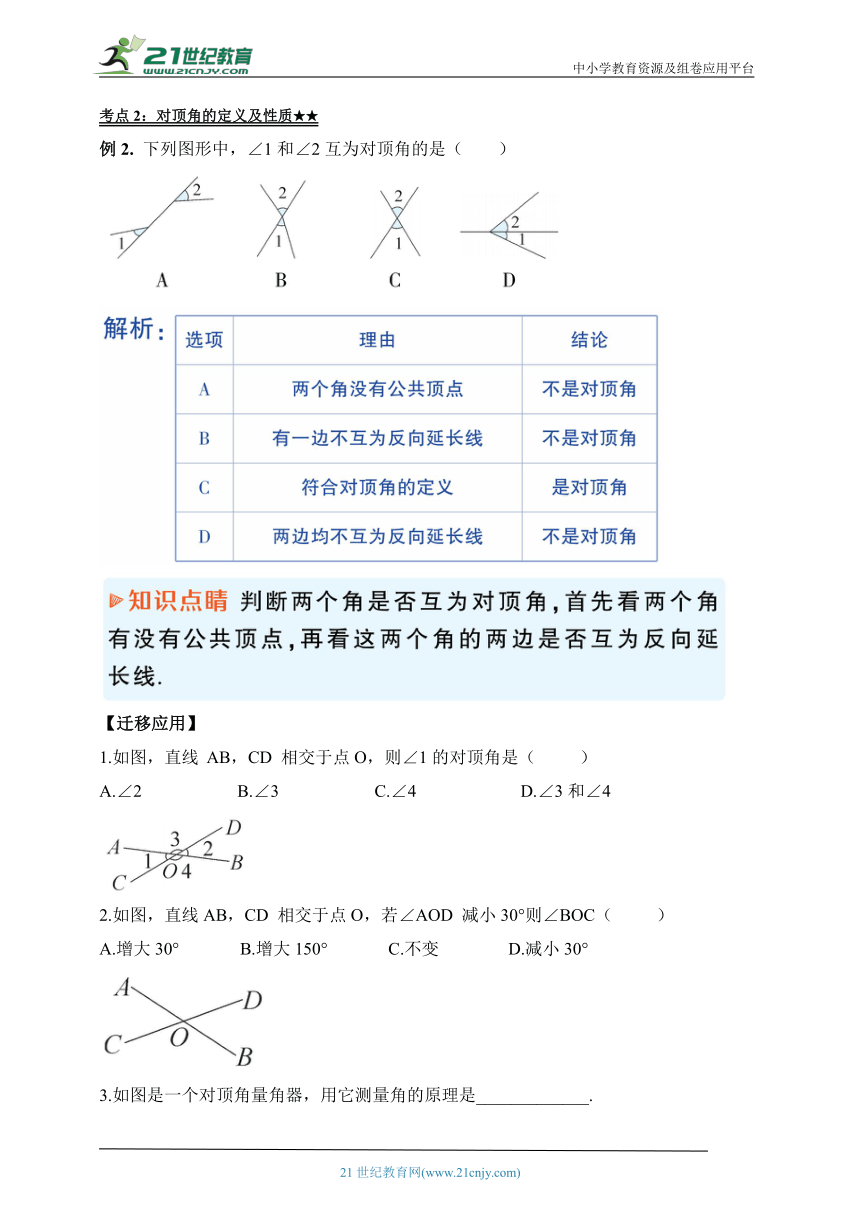
思考:作过程,你能发现它的角有什么变化?如果把剪刀的构造看做两条相交的直线,你们想想它是一种怎样的几何结构?
如果两条直线有一个公共点,就说这两条直线相交;公共点叫做这两条直线的交点.
上图的几何描述为:直线AB、CD相交于点O.
合作探究
探究:任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类.
形如∠1与∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
图中还有哪些角也是邻补角呢?
形如∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
∠1 与∠3在数量上又有什么关系呢?
对顶角相等
∵ ∠1与∠2互补,∠3与∠2互补 (邻补角的定义)
∴ ∠1=∠3 (同角的补角相等)
(注:“∵”表示“因为”,“∴”表示“所以”.)
考点解析
考点1:邻补角的定义及性质★
例1. 下列图形中,∠1与∠2互为邻补角的是( )
【迁移应用】
1.下列说法中正确的是( )
A.一个角的邻补角只有
B.一个角的邻补角必定大于这个角
C.相等的两个角不可能是邻补角
D.一个角的邻补角可能是锐角、钝角或直角
2.如图,直线a,b相交.
(1)∠1+∠2=_____°;∠3+∠4=____°.
(2)∠4的邻补角是_________.
(3)图中的邻补角共有_____对.
3. 已知∠B与∠A 互为邻补角,且∠B=2∠A,那么∠A=_____°.
考点2:对顶角的定义及性质★★
例2. 下列图形中,∠1和∠2互为对顶角的是( )
【迁移应用】
1.如图,直线 AB,CD 相交于点O,则∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠3和∠4
2.如图,直线AB,CD 相交于点O,若∠AOD 减小30°则∠BOC( )
A.增大30° B.增大150° C.不变 D.减小30°
3.如图是一个对顶角量角器,用它测量角的原理是_____________.
4.如图是一把剪刀,若∠AOB+∠COD=82°,则∠BOD=________.
5.如图,直线AB,CD相交于点O,∠AOC=(2x-10)°,∠BOD=(x+25)°,则x=_______.
考点3:运用邻补角、对顶角的性质进行角度的计算★★★
例3.【方程思想】如图,直线AB,CD相交于点O,∠AOC = 80°,OE把∠BOD分成两部分,且∠BOE:∠DOE=2:3,求∠AOE的度数.
解:因为∠AOC=80°,∠AOC=∠BOD(对顶角相等),
所以∠BOD=80°.
由∠BOE:∠DOE=2∶3,
设∠BOE=2x°,∠DOE=3x° .
因为∠BOD=∠BOE+∠DOE,
所以2x+3x=80,
解得x=16.
【迁移应用】
1.如图,直线AB与CD 相交于点O,OA 平分∠COE,若∠DOE=70°,则∠BOD 的度数是( )
A.75° B.65° C.55° D.105°
2.如图,三条直线相交于一点,则 ∠1+∠2+ ∠3 =_____°.
3.如图直线AB,CD相交于点O,OA 平分∠EOC.若∠EOA:∠EOD=1:3,求∠BOD的度数.
解:因为∠EOA: ∠EOD=1:3,
所以设∠EOA=x°,∠EOD= 3x°
因为OA平分∠EOC
所以∠COA=∠EOA=x°,∠EOC=2x°
因为∠EOC+∠EOD=180°(邻补角的定义).
所以 2x+3x=180,
解得 x=36.
所∠COA=36°
所以∠BOD=∠COA=36°(对顶角相等)
考点4:利用邻补角与对顶角的性质解决实际问题★★★
例4.【一题多解】如图是一块弯折的屏风,假设其背面不可到达,要测量其在地面上形成的∠AOB的度数,你有什么方法?
解:方法 1:
如图①,延长 AO 至点 C,测量出 ∠BOC 的度数.
因为邻补角互补,所以 ∠AOB+ ∠BOC = 180°,所以 ∠AOB =180°- ∠BOC,即可得到 ∠AOB 的度数.
方法2:如图②,延长AO至点C,延长BO至点D,测量出∠COD的度数.
因为对顶角相等,所以∠AOB=∠COD,即可得到∠AOB的度数.
【迁移应用】
【跨学科】将一根玻璃棒放入盛有水的烧杯中,一头露出水面,一头浸入水中,我们可以发现浸入水中的部分“变弯了”.它真的变弯了吗? 其实没有,这只是光的折射现象,即光从空气射入水中,光线的传播方向发生改变如图,一束光AO射入水中,在水中的传播路径为OB,∠1与∠2是对顶角吗?如果不是对顶角,你能比较它们的大小吗?
解:∠1与∠2不是对顶角.
如图,延长AO,可得∠2>∠1.
考点5:邻补角在折叠问题中的应用★★★★
例5.【整体思想】如图,将五边形纸片ABCDE折叠,折痕为AF,点D,E分别落在点D′,E′处.已知∠AFC=76°,求∠CFD′的度数.
解:因为∠AFC+∠AFD=180°(邻补角的定义),
∠AFC=76°,
所以∠AFD=180°-∠AFC=104°.
由折叠可知∠AFD′=∠AFD=104°,
所以∠CFD′=∠AFD′- ∠AFC =104°-76°=28°.
【迁移应用】
1. 如图,把一张长方形的纸片按如图所示的方式折叠后,B,D两点分别落在点B′,D′处.若∠AOB′=80°,则∠B′OG的度数为_______.
2.如图,将长方形纸片折叠,使点A落在点A′处,BC为折痕,BD为∠A′BE的平分线,则∠CBD的度数为________.
考点6:相交线中的探究题★★★★★
例6. (1)观察图①,图中共有____对对顶角,_____对邻补角;
(2)观察图②,图中共有_____对对顶角,_____对邻补角;
(3)观察图③,图中共有_____对对顶角,_____对邻补角;
(4)若有n条直线相交于一点,则可形成________对对顶角,________对邻补角.
解:(1)图①中,共有对顶角1×2=2(对),邻补角2×1×2=4(对);
(2)图②中,共有对顶角2×3=6(对),邻补角2×2×3=12(对) ;
(3)图③中,共有对顶角3×4=12(对),邻补角2×3×4=24(对);
(4)由特殊到一般,可找出规律:若有n条直线相交于一点,则可形成n ( n-1 )对对顶角,2n (n-1)对邻补角.
【迁移应用】
观察下列图形,阅读下面的相关文字并回答后面的问题:
(1)5条直线相交,最多有几个交点?
(2)6条直线相交,最多有几个交点?
(3)猜想:n条直线相交,最多有几个交点?
解:(1)5条直线相交,交点最多有=10(个).
(2)6 条直线相交,交点最多有=15(个).
(3) n条直线相交,最多有个交点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1.1 相交线 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线”5.1.1相交线,内容包括:邻补角与对顶角的概念及性质.
2.内容解析
本节课是在学习了直线、射线、线段和角的有关知识的基础上,进一步研究平面内两条直线相交形成4个角的位置和数量关系,为今后学习几何奠定了基础,同时也为证明几何题提供了一个示范作用,本节对于进一步培养学生的识图能力,激发学生的学习兴趣具有推动作用,所以本节课具有很重要的地位和作用。
基于以上分析,确定本节课的教学重点为:掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
二、目标和目标解析
1.目标
(1)理解两条直线相交的特征及邻补角与对顶角的概念.
(2)掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
2.目标解析
理解对顶角和邻补角的概念,能从图中辨别对顶角和邻补角。掌握“对顶角相等的性质”,理解对顶角相等的说理过程,在数学活动中培养学生的观察、转化、说理能力和语言规范表达能力。通过小组讨论,培养合作精神,让学生在探索问题的过程中,体验解决问题的方法和乐趣,增强学习兴趣;在解题中感受生活中数学的存在,体验数学中充满着探索和创造。
三、教学问题诊断分析
七年级的孩子思维活跃,模仿能力强。同时他们也具备了一定的学习能力,在老师的指导下,能针对某一问题展开讨论并归纳总结。但是受年龄特征的影响,他们对知识迁移能力不强,推理能力还需进一步培养。
基于以上学情分析,掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单的实际问题.
四、教学过程设计
情境引入
你能在身边找出一些相交线的实例吗?
自学导航
思考:作过程,你能发现它的角有什么变化?如果把剪刀的构造看做两条相交的直线,你们想想它是一种怎样的几何结构?
如果两条直线有一个公共点,就说这两条直线相交;公共点叫做这两条直线的交点.
上图的几何描述为:直线AB、CD相交于点O.
合作探究
探究:任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类.
形如∠1与∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角.
图中还有哪些角也是邻补角呢?
形如∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
图中还有哪些角也是对顶角呢?
∠1 与∠3在数量上又有什么关系呢?
对顶角相等
∵ ∠1与∠2互补,∠3与∠2互补 (邻补角的定义)
∴ ∠1=∠3 (同角的补角相等)
(注:“∵”表示“因为”,“∴”表示“所以”.)
考点解析
考点1:邻补角的定义及性质★
例1. 下列图形中,∠1与∠2互为邻补角的是( )
【迁移应用】
1.下列说法中正确的是( )
A.一个角的邻补角只有
B.一个角的邻补角必定大于这个角
C.相等的两个角不可能是邻补角
D.一个角的邻补角可能是锐角、钝角或直角
2.如图,直线a,b相交.
(1)∠1+∠2=_____°;∠3+∠4=____°.
(2)∠4的邻补角是_________.
(3)图中的邻补角共有_____对.
3. 已知∠B与∠A 互为邻补角,且∠B=2∠A,那么∠A=_____°.
考点2:对顶角的定义及性质★★
例2. 下列图形中,∠1和∠2互为对顶角的是( )
【迁移应用】
1.如图,直线 AB,CD 相交于点O,则∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠3和∠4
2.如图,直线AB,CD 相交于点O,若∠AOD 减小30°则∠BOC( )
A.增大30° B.增大150° C.不变 D.减小30°
3.如图是一个对顶角量角器,用它测量角的原理是_____________.
4.如图是一把剪刀,若∠AOB+∠COD=82°,则∠BOD=________.
5.如图,直线AB,CD相交于点O,∠AOC=(2x-10)°,∠BOD=(x+25)°,则x=_______.
考点3:运用邻补角、对顶角的性质进行角度的计算★★★
例3.【方程思想】如图,直线AB,CD相交于点O,∠AOC = 80°,OE把∠BOD分成两部分,且∠BOE:∠DOE=2:3,求∠AOE的度数.
解:因为∠AOC=80°,∠AOC=∠BOD(对顶角相等),
所以∠BOD=80°.
由∠BOE:∠DOE=2∶3,
设∠BOE=2x°,∠DOE=3x° .
因为∠BOD=∠BOE+∠DOE,
所以2x+3x=80,
解得x=16.
【迁移应用】
1.如图,直线AB与CD 相交于点O,OA 平分∠COE,若∠DOE=70°,则∠BOD 的度数是( )
A.75° B.65° C.55° D.105°
2.如图,三条直线相交于一点,则 ∠1+∠2+ ∠3 =_____°.
3.如图直线AB,CD相交于点O,OA 平分∠EOC.若∠EOA:∠EOD=1:3,求∠BOD的度数.
解:因为∠EOA: ∠EOD=1:3,
所以设∠EOA=x°,∠EOD= 3x°
因为OA平分∠EOC
所以∠COA=∠EOA=x°,∠EOC=2x°
因为∠EOC+∠EOD=180°(邻补角的定义).
所以 2x+3x=180,
解得 x=36.
所∠COA=36°
所以∠BOD=∠COA=36°(对顶角相等)
考点4:利用邻补角与对顶角的性质解决实际问题★★★
例4.【一题多解】如图是一块弯折的屏风,假设其背面不可到达,要测量其在地面上形成的∠AOB的度数,你有什么方法?
解:方法 1:
如图①,延长 AO 至点 C,测量出 ∠BOC 的度数.
因为邻补角互补,所以 ∠AOB+ ∠BOC = 180°,所以 ∠AOB =180°- ∠BOC,即可得到 ∠AOB 的度数.
方法2:如图②,延长AO至点C,延长BO至点D,测量出∠COD的度数.
因为对顶角相等,所以∠AOB=∠COD,即可得到∠AOB的度数.
【迁移应用】
【跨学科】将一根玻璃棒放入盛有水的烧杯中,一头露出水面,一头浸入水中,我们可以发现浸入水中的部分“变弯了”.它真的变弯了吗? 其实没有,这只是光的折射现象,即光从空气射入水中,光线的传播方向发生改变如图,一束光AO射入水中,在水中的传播路径为OB,∠1与∠2是对顶角吗?如果不是对顶角,你能比较它们的大小吗?
解:∠1与∠2不是对顶角.
如图,延长AO,可得∠2>∠1.
考点5:邻补角在折叠问题中的应用★★★★
例5.【整体思想】如图,将五边形纸片ABCDE折叠,折痕为AF,点D,E分别落在点D′,E′处.已知∠AFC=76°,求∠CFD′的度数.
解:因为∠AFC+∠AFD=180°(邻补角的定义),
∠AFC=76°,
所以∠AFD=180°-∠AFC=104°.
由折叠可知∠AFD′=∠AFD=104°,
所以∠CFD′=∠AFD′- ∠AFC =104°-76°=28°.
【迁移应用】
1. 如图,把一张长方形的纸片按如图所示的方式折叠后,B,D两点分别落在点B′,D′处.若∠AOB′=80°,则∠B′OG的度数为_______.
2.如图,将长方形纸片折叠,使点A落在点A′处,BC为折痕,BD为∠A′BE的平分线,则∠CBD的度数为________.
考点6:相交线中的探究题★★★★★
例6. (1)观察图①,图中共有____对对顶角,_____对邻补角;
(2)观察图②,图中共有_____对对顶角,_____对邻补角;
(3)观察图③,图中共有_____对对顶角,_____对邻补角;
(4)若有n条直线相交于一点,则可形成________对对顶角,________对邻补角.
解:(1)图①中,共有对顶角1×2=2(对),邻补角2×1×2=4(对);
(2)图②中,共有对顶角2×3=6(对),邻补角2×2×3=12(对) ;
(3)图③中,共有对顶角3×4=12(对),邻补角2×3×4=24(对);
(4)由特殊到一般,可找出规律:若有n条直线相交于一点,则可形成n ( n-1 )对对顶角,2n (n-1)对邻补角.
【迁移应用】
观察下列图形,阅读下面的相关文字并回答后面的问题:
(1)5条直线相交,最多有几个交点?
(2)6条直线相交,最多有几个交点?
(3)猜想:n条直线相交,最多有几个交点?
解:(1)5条直线相交,交点最多有=10(个).
(2)6 条直线相交,交点最多有=15(个).
(3) n条直线相交,最多有个交点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
