【2024春人教七下数学精品教案】5.1.2 垂线
文档属性
| 名称 | 【2024春人教七下数学精品教案】5.1.2 垂线 |

|
|
| 格式 | docx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 12:48:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.1.2 垂线 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”) 第五章“相交线与平行线”5.1.2垂线,内容包括:垂线的有关概念、性质及画法、垂线段和点到直线的距离的概念.
2.内容解析
垂线是平面几何所要研究的基本内容之一.垂线的概念、画法和性质是重要的基础知识,是进一步学习平面直角坐标系、三角形的高、切线的性质和判定、以及空间里的垂直关系等知识的基础,与其他数学知识一样,它在现实生活中有着广泛的应用.垂线的概念和性质,蕴含着“从一般到特殊”的认识规律,是培养学生思维能力的重要内容之一.
基于以上分析,确定本节课的教学重点为:垂直定义、垂直性质的理解与运用.
二、目标和目标解析
1.目标
(1)理解垂线的有关概念、性质及画法;
(2)知道垂线段和点到直线的距离的概念,并会应用其解决问题.
2.目标解析
认识垂线,理解“互相垂直”和“垂足”的含义;会用三角板或量角器过一点画一条直线(或射线、线段)的垂线:3.知道垂线的性质:过一点有且只有一条直线垂直于已知直线;培养学生的观察、理解能力,几何语言能力,画图能力,抽象思维能力;培养学生动手操作能力和创造精神,运用知识解决实际问题能力,形成垂线的空间观念;培养学生辩证唯物主义思想及勇于探索的精神;培养学生的合作精神,进行集体观念的教育.
三、教学问题诊断分析
七年级学生是第三学段低年级的学生,他们在课堂中思维活跃,有想法就会举手发言甚至是抢答,探索真理的欲望比较强.因此,我们要营造轻松、和谐的课堂气氛,充分激活学生的探索欲望,让学生在教师创设的情境中充满好奇地学,留给学生足够的自主活动、相互交流的空间,让学生在观察中不断发现数学问题、在实践中领悟数学思想、在评价中逐步形成数学价值观.七年级学生由于年龄较小,他们虽然对新事物容易产生兴趣,但这种兴趣并不稳定,上课时注意力也不易持久,容易分散,因而在教学中不断激发他们的兴趣,吸引他们的注意力至关重要。我采用生动形象多媒体教学,给学生以动感,既加深了理解,也不断地引发学生的兴趣.
基于以上学情分析,确定本节课的教学难点为:能利用垂线的性质进行简单的推理.
四、教学过程设计
情境引入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
自学导航
在相交线的模型中,固定木条 a ,转动木条 b.当 b的位置变化时,a、b 所成的角
∠α也会发生变化.
当∠α=90°时,我们说 a 与 b互相垂直,记作 a⊥b.
当两条直线相交所构成的四个角中有一个是直角,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线;互相垂直的两条直线的交点叫做垂足.
如上图,直线AB与直线CD垂直,记作:AB⊥CD,垂足是O;
直线 m 与直线 n 垂直,记作:m⊥n;
“⊥”是“垂直”的记号,读作“垂直于”;
而“┐”是图形中“垂直”(直角)的标记.
垂直的定义有以下两层含义:
1.∵AB⊥CD (已知) 2.∵∠1=90°(已知)
∴∠1=90°(垂直的定义) ∴AB⊥CD (垂直的定义)
日常生活中,两条直线互相垂直的情形很常见,说出下图中的一些互相垂直的木条.
你能再举出其他例子吗?
做一做
1.你能借助三角尺画出两条互相垂直的直线吗?
2.如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
3.利用下面的方法可以折出互相垂直的线,你试试看!
合作探究
1.用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
2.经过直线 l 上一点A画 l 的垂线,这样的垂线能画出几条?
3.经过直线 l 外一点B画 l 的垂线,这样的垂线能画出几条?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线. 即在同一平面内,过一点有且只有一条直线与已知直线垂直.
考点解析
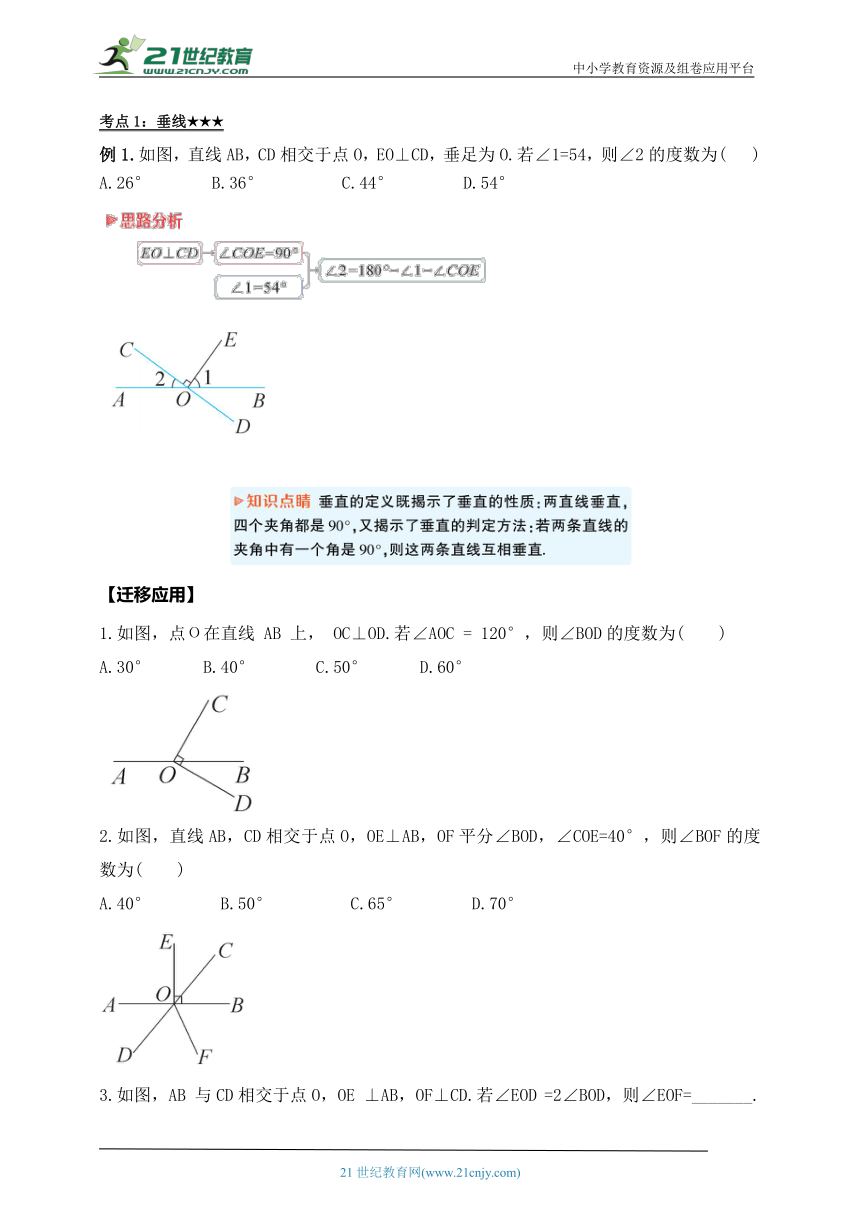
考点1:垂线★★★
例1.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【迁移应用】
1.如图,点О在直线 AB 上, OC⊥OD.若∠AOC = 120°,则∠BOD的度数为( )
A.30° B.40° C.50° D.60°
2.如图,直线AB,CD相交于点O,OE⊥AB,OF平分∠BOD,∠COE=40°,则∠BOF的度数为( )
A.40° B.50° C.65° D.70°
3.如图,AB 与CD相交于点O,OE ⊥AB,OF⊥CD.若∠EOD =2∠BOD,则∠EOF=_______.
4.已知OA ⊥OC,∠AOB :∠BOC =1:3,则∠BOC的度数为______________.
考点2:垂线的画法★★★
例2.如图,在三角形ABC中,过点B画边AC的垂线,下列画法正确的是( )
【迁移应用】
1.下列各图中,过直线l外一点Р画l的垂线CD,操作三角尺的方法正确的是( )
2.如图,过点P分别画出OA,OB的垂线.
合作探究
思考:如图,在灌溉时,要把河中的水引到农田P处如何挖渠能使渠道最短?
探究:如图,连接直线 l 外一点P与直线 l 上各点O,A1,A2,A3,A4,A5,…,其中PO⊥l (我们称PO为点P到直线 l 的垂线段).比较线段PO,PA1,PA2,PA3,PA4,PA5,…的长短,这些线段中,哪一条最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
现在,你知道水渠该怎么挖了吗?在书中图5.1-8中画出来,如果图中比例尺为1:100000,水渠大约要挖多长?
则:沿着垂线段PH挖渠能使渠道最短.
我们如何测量立定跳远的成绩?
考点解析
考点3:垂线、垂线段的性质★★★
例3.如图,在三角形ABC中,AB⊥BC,其中AC=2.5,AB=1,P是线段BC上任意一点,那么线段AP的长度可能为( )
A.0.5 B.0.7 C.1.5 D.4
解析:因为Р是线段BC上任意一点,且AB⊥BC,根据“垂线段最短”可知线段BC上的所有点中,与点A的距离最近的为点B,即线段AP的长度最短为1;与点A的距离最远的为点C,即线段AP的长度最长为2.5,所以1≤AP≤2.5,选项中满足条件的只有1.5.
【迁移应用】
1.如图,AC⊥BC,AD⊥CD,垂足分别为C,D.若AD=4,AB=7,则AC的长可能是( )
A.4 B.6 C.7 D.8
2.如图,测量运动员跳远成绩选取的是线段AB的长度,其依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间,线段最短 D.垂直的定义
3.如图,AB⊥MN,BC⊥MN,垂足都是B,那么A,B,C三点在一条直线上,其依据是________________________________________________________.
考点4:点到直线的距离★★★★
例4. 如图,AB⊥AC, AD⊥BC,其中AC=4,AB=3,BC=5,AD=,CD=,则点B到AD的距离为( )
A.3 B.5 C. D.
【迁移应用】
1.P为直线m外一点,A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2 cm,则点P到直线m的距离( )
A.等于4cm B.等于2cm C.小于2cm D.不大于2cm
2.如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AC=10,AB =6,BC=8,则点B到直线AC的距离为______.
考点5:利用垂直的定义判断两直线的位置关系★★★★★
例5. 如图,O是直线AB 上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,并说明理由.
解:(1)因为∠AOC=∠BOC,
所以∠BOC=3∠AOC.
因为∠AOC+∠BOC=180°,
所以∠AOC+3∠AOC=180°,
所以∠AOC=45°.
因为OC是∠AOD的平分线,
所以∠COD= ∠AOC=45°.
(2)OD⊥AB.
理由如下:
由(1)知∠COD=∠AOC=45°,
所以∠AOD=∠COD+∠AOC=90°,
所以OD⊥AB.
【迁移应用】
1.如图,直线AB,CD相交于点O,OE为射线.若∠1= 30°, ∠2=120°,则OE与AB的位置关系是_____________.
2.如图,直线AB,CD相交于点O,OM⊥AB.若∠1=∠2,判断ON 与CD的位置关系,并说明理由.
解:ON⊥CD.理由如下:
因为OM⊥AB,
所以∠AOM=90°,
所以∠1+ ∠AOC=90°.
因为∠1= ∠2,
所以∠2+ ∠AOC=90°.
即∠CON=90°,所以ON⊥CD.
3.如图,已知O为直线AB 上一点, OE平分∠BOC,OD平分∠AOC,则OE与OD有什么位置关系 为什么
解:OE⊥OD.理由如下:
因为OE平分∠BOC,OD平分∠AOC,
所以∠COE =∠BOC, ∠COD=∠AOC.
因为∠AOC+∠BOC=180°,
所以∠COD+∠COE= (∠AOC+∠BOC)=180°=90°,
即∠DOE=90°,所以OE⊥OD.
考点5:利用垂直的定义判断两直线的位置关系★★★★★
例6.【分类讨论思想】如图,直线AB,CD相交于点O,OE⊥CD.
(1)若∠BOD:∠BOC=1∶4,求∠AOE的度数;
(2)在(1)的条件下,过D点О作OF⊥AB,求∠EOF的度数.
解:(1)因为∠BOD∶∠BOC=1∶4,∠BOD+∠BOC=180°.
所以∠BOD=180×=36°,
所以∠AOC=∠BOD=36°.
因为OE⊥CD,所以∠COE=90°,
所以∠AOE=∠AOC+∠COE=126°.
(2)因为OE⊥CD,所以∠EOD=90°.
因为∠ BOD=36°,
所以∠EOB=∠EOD-∠BOD=54°.
分两种情况讨论:
①如图①,当OF在AB的下方时,
因为OF⊥AB,所以∠BOF=90°,
所以∠EOF=∠BOF+∠EOB=144°;
②如图②,当OF在AB的上方时,
因为OF⊥AB,所以∠BOF=90°,
所以∠EOF=∠BOF- ∠EOB=36°.
综上所述,∠EOF的度数为144°或36°.
【迁移应用】
1.如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,∠AOE = 24°,则∠COF的度数是( )
A.146° B.147° C.157° D.136°
2.在直线AB上任取一点O,过点О作射线OC,OD,使OC⊥OD于点O.当∠AOC=30°时,∠BOD的度数为( )
A.60° B.120° C.60°或90° D.60°或120°
3.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠AOF的度数;
(2)若∠BOD: ∠BOE=4∶3,求∠AOF的度数.
解:(1)因为OE平分∠BOC,∠BOE=60°,
所以∠BOC=2∠BOE=120°,
所以∠AOC=180°-∠BOC=60°.
因为OF⊥CD,所以∠COF=90°
所以∠AOF=∠COF-∠AOC=90°-60°=30°.
(2)因为OE平分∠BOC,所以∠BOE= ∠COE.
因为∠BOD: ∠BOE=4∶3,所以设∠BOD=4x°,
则∠ BOE=3x°,所以∠COE=3x°.
因为∠BOD+ ∠BOE+ ∠COE=180°.
所以4x+3x+3x=180,解得x=18.
所以∠BOD=4×18°=72°,所以∠AOC=∠BOD=72°.
因为OF⊥CD,所以∠COF=90°,
所以∠AOF= ∠COF- ∠AOC=90°-72°=18°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1.2 垂线 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”) 第五章“相交线与平行线”5.1.2垂线,内容包括:垂线的有关概念、性质及画法、垂线段和点到直线的距离的概念.
2.内容解析
垂线是平面几何所要研究的基本内容之一.垂线的概念、画法和性质是重要的基础知识,是进一步学习平面直角坐标系、三角形的高、切线的性质和判定、以及空间里的垂直关系等知识的基础,与其他数学知识一样,它在现实生活中有着广泛的应用.垂线的概念和性质,蕴含着“从一般到特殊”的认识规律,是培养学生思维能力的重要内容之一.
基于以上分析,确定本节课的教学重点为:垂直定义、垂直性质的理解与运用.
二、目标和目标解析
1.目标
(1)理解垂线的有关概念、性质及画法;
(2)知道垂线段和点到直线的距离的概念,并会应用其解决问题.
2.目标解析
认识垂线,理解“互相垂直”和“垂足”的含义;会用三角板或量角器过一点画一条直线(或射线、线段)的垂线:3.知道垂线的性质:过一点有且只有一条直线垂直于已知直线;培养学生的观察、理解能力,几何语言能力,画图能力,抽象思维能力;培养学生动手操作能力和创造精神,运用知识解决实际问题能力,形成垂线的空间观念;培养学生辩证唯物主义思想及勇于探索的精神;培养学生的合作精神,进行集体观念的教育.
三、教学问题诊断分析
七年级学生是第三学段低年级的学生,他们在课堂中思维活跃,有想法就会举手发言甚至是抢答,探索真理的欲望比较强.因此,我们要营造轻松、和谐的课堂气氛,充分激活学生的探索欲望,让学生在教师创设的情境中充满好奇地学,留给学生足够的自主活动、相互交流的空间,让学生在观察中不断发现数学问题、在实践中领悟数学思想、在评价中逐步形成数学价值观.七年级学生由于年龄较小,他们虽然对新事物容易产生兴趣,但这种兴趣并不稳定,上课时注意力也不易持久,容易分散,因而在教学中不断激发他们的兴趣,吸引他们的注意力至关重要。我采用生动形象多媒体教学,给学生以动感,既加深了理解,也不断地引发学生的兴趣.
基于以上学情分析,确定本节课的教学难点为:能利用垂线的性质进行简单的推理.
四、教学过程设计
情境引入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
自学导航
在相交线的模型中,固定木条 a ,转动木条 b.当 b的位置变化时,a、b 所成的角
∠α也会发生变化.
当∠α=90°时,我们说 a 与 b互相垂直,记作 a⊥b.
当两条直线相交所构成的四个角中有一个是直角,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线;互相垂直的两条直线的交点叫做垂足.
如上图,直线AB与直线CD垂直,记作:AB⊥CD,垂足是O;
直线 m 与直线 n 垂直,记作:m⊥n;
“⊥”是“垂直”的记号,读作“垂直于”;
而“┐”是图形中“垂直”(直角)的标记.
垂直的定义有以下两层含义:
1.∵AB⊥CD (已知) 2.∵∠1=90°(已知)
∴∠1=90°(垂直的定义) ∴AB⊥CD (垂直的定义)
日常生活中,两条直线互相垂直的情形很常见,说出下图中的一些互相垂直的木条.
你能再举出其他例子吗?
做一做
1.你能借助三角尺画出两条互相垂直的直线吗?
2.如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?
3.利用下面的方法可以折出互相垂直的线,你试试看!
合作探究
1.用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?
2.经过直线 l 上一点A画 l 的垂线,这样的垂线能画出几条?
3.经过直线 l 外一点B画 l 的垂线,这样的垂线能画出几条?
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线. 即在同一平面内,过一点有且只有一条直线与已知直线垂直.
考点解析
考点1:垂线★★★
例1.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【迁移应用】
1.如图,点О在直线 AB 上, OC⊥OD.若∠AOC = 120°,则∠BOD的度数为( )
A.30° B.40° C.50° D.60°
2.如图,直线AB,CD相交于点O,OE⊥AB,OF平分∠BOD,∠COE=40°,则∠BOF的度数为( )
A.40° B.50° C.65° D.70°
3.如图,AB 与CD相交于点O,OE ⊥AB,OF⊥CD.若∠EOD =2∠BOD,则∠EOF=_______.
4.已知OA ⊥OC,∠AOB :∠BOC =1:3,则∠BOC的度数为______________.
考点2:垂线的画法★★★
例2.如图,在三角形ABC中,过点B画边AC的垂线,下列画法正确的是( )
【迁移应用】
1.下列各图中,过直线l外一点Р画l的垂线CD,操作三角尺的方法正确的是( )
2.如图,过点P分别画出OA,OB的垂线.
合作探究
思考:如图,在灌溉时,要把河中的水引到农田P处如何挖渠能使渠道最短?
探究:如图,连接直线 l 外一点P与直线 l 上各点O,A1,A2,A3,A4,A5,…,其中PO⊥l (我们称PO为点P到直线 l 的垂线段).比较线段PO,PA1,PA2,PA3,PA4,PA5,…的长短,这些线段中,哪一条最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
现在,你知道水渠该怎么挖了吗?在书中图5.1-8中画出来,如果图中比例尺为1:100000,水渠大约要挖多长?
则:沿着垂线段PH挖渠能使渠道最短.
我们如何测量立定跳远的成绩?
考点解析
考点3:垂线、垂线段的性质★★★
例3.如图,在三角形ABC中,AB⊥BC,其中AC=2.5,AB=1,P是线段BC上任意一点,那么线段AP的长度可能为( )
A.0.5 B.0.7 C.1.5 D.4
解析:因为Р是线段BC上任意一点,且AB⊥BC,根据“垂线段最短”可知线段BC上的所有点中,与点A的距离最近的为点B,即线段AP的长度最短为1;与点A的距离最远的为点C,即线段AP的长度最长为2.5,所以1≤AP≤2.5,选项中满足条件的只有1.5.
【迁移应用】
1.如图,AC⊥BC,AD⊥CD,垂足分别为C,D.若AD=4,AB=7,则AC的长可能是( )
A.4 B.6 C.7 D.8
2.如图,测量运动员跳远成绩选取的是线段AB的长度,其依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间,线段最短 D.垂直的定义
3.如图,AB⊥MN,BC⊥MN,垂足都是B,那么A,B,C三点在一条直线上,其依据是________________________________________________________.
考点4:点到直线的距离★★★★
例4. 如图,AB⊥AC, AD⊥BC,其中AC=4,AB=3,BC=5,AD=,CD=,则点B到AD的距离为( )
A.3 B.5 C. D.
【迁移应用】
1.P为直线m外一点,A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2 cm,则点P到直线m的距离( )
A.等于4cm B.等于2cm C.小于2cm D.不大于2cm
2.如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为D,AC=10,AB =6,BC=8,则点B到直线AC的距离为______.
考点5:利用垂直的定义判断两直线的位置关系★★★★★
例5. 如图,O是直线AB 上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,并说明理由.
解:(1)因为∠AOC=∠BOC,
所以∠BOC=3∠AOC.
因为∠AOC+∠BOC=180°,
所以∠AOC+3∠AOC=180°,
所以∠AOC=45°.
因为OC是∠AOD的平分线,
所以∠COD= ∠AOC=45°.
(2)OD⊥AB.
理由如下:
由(1)知∠COD=∠AOC=45°,
所以∠AOD=∠COD+∠AOC=90°,
所以OD⊥AB.
【迁移应用】
1.如图,直线AB,CD相交于点O,OE为射线.若∠1= 30°, ∠2=120°,则OE与AB的位置关系是_____________.
2.如图,直线AB,CD相交于点O,OM⊥AB.若∠1=∠2,判断ON 与CD的位置关系,并说明理由.
解:ON⊥CD.理由如下:
因为OM⊥AB,
所以∠AOM=90°,
所以∠1+ ∠AOC=90°.
因为∠1= ∠2,
所以∠2+ ∠AOC=90°.
即∠CON=90°,所以ON⊥CD.
3.如图,已知O为直线AB 上一点, OE平分∠BOC,OD平分∠AOC,则OE与OD有什么位置关系 为什么
解:OE⊥OD.理由如下:
因为OE平分∠BOC,OD平分∠AOC,
所以∠COE =∠BOC, ∠COD=∠AOC.
因为∠AOC+∠BOC=180°,
所以∠COD+∠COE= (∠AOC+∠BOC)=180°=90°,
即∠DOE=90°,所以OE⊥OD.
考点5:利用垂直的定义判断两直线的位置关系★★★★★
例6.【分类讨论思想】如图,直线AB,CD相交于点O,OE⊥CD.
(1)若∠BOD:∠BOC=1∶4,求∠AOE的度数;
(2)在(1)的条件下,过D点О作OF⊥AB,求∠EOF的度数.
解:(1)因为∠BOD∶∠BOC=1∶4,∠BOD+∠BOC=180°.
所以∠BOD=180×=36°,
所以∠AOC=∠BOD=36°.
因为OE⊥CD,所以∠COE=90°,
所以∠AOE=∠AOC+∠COE=126°.
(2)因为OE⊥CD,所以∠EOD=90°.
因为∠ BOD=36°,
所以∠EOB=∠EOD-∠BOD=54°.
分两种情况讨论:
①如图①,当OF在AB的下方时,
因为OF⊥AB,所以∠BOF=90°,
所以∠EOF=∠BOF+∠EOB=144°;
②如图②,当OF在AB的上方时,
因为OF⊥AB,所以∠BOF=90°,
所以∠EOF=∠BOF- ∠EOB=36°.
综上所述,∠EOF的度数为144°或36°.
【迁移应用】
1.如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,∠AOE = 24°,则∠COF的度数是( )
A.146° B.147° C.157° D.136°
2.在直线AB上任取一点O,过点О作射线OC,OD,使OC⊥OD于点O.当∠AOC=30°时,∠BOD的度数为( )
A.60° B.120° C.60°或90° D.60°或120°
3.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠AOF的度数;
(2)若∠BOD: ∠BOE=4∶3,求∠AOF的度数.
解:(1)因为OE平分∠BOC,∠BOE=60°,
所以∠BOC=2∠BOE=120°,
所以∠AOC=180°-∠BOC=60°.
因为OF⊥CD,所以∠COF=90°
所以∠AOF=∠COF-∠AOC=90°-60°=30°.
(2)因为OE平分∠BOC,所以∠BOE= ∠COE.
因为∠BOD: ∠BOE=4∶3,所以设∠BOD=4x°,
则∠ BOE=3x°,所以∠COE=3x°.
因为∠BOD+ ∠BOE+ ∠COE=180°.
所以4x+3x+3x=180,解得x=18.
所以∠BOD=4×18°=72°,所以∠AOC=∠BOD=72°.
因为OF⊥CD,所以∠COF=90°,
所以∠AOF= ∠COF- ∠AOC=90°-72°=18°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
