【2024春人教七下数学精品教案】5_1_3 同位角、内错角、同旁内角
文档属性
| 名称 | 【2024春人教七下数学精品教案】5_1_3 同位角、内错角、同旁内角 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 14:25:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1.3 同位角、内错角、同旁内角 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线”5.1.3 同位角、内错角、同旁内角,内容包括:同位角、内错角、同旁内角的概念及辨识.
2.内容解析
本节内容主要是学习同位角、内错角、同旁内角的概念,在研究了两条相交直线构成的角(对顶角,邻补角)的基础上进一步探究平面内三条直线相交形成的不共顶点的角的位置关系,主要学习同位角、内错角、同旁内角的概念.它是进一步学习平行线的判定和性质的必要准备.
教科书通过两条直线相交的四个角的知识为基础,引出一条直线分别与两条直线相交构成的八个角中,通过分类讨论思想,把不共顶点的两个角的位置关系分为同位角、内错角、同旁内角三类.紧接着,通过一个例题来让学生学习同位角、内错角、同旁内角的概念,教学时可根据情况适当要求学生说明同位角、内错角与同旁内角是哪两条直线被哪一条直线所截得到的,为后面学习平行线的性质与判定做好铺垫.
基于以上分析,确定本节课的教学重点为:理解同位角、内错角、同旁内角的概念.
二、目标和目标解析
1.目标
(1)理解同位角、内错角、同旁内角的概念;
(2)结合图形识别同位角、内错角、同旁内角;
(3)从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.
2.目标解析
理解同位角、内错角、同旁内角的概念结合图形识别同位角、内错角、同旁内角;通过变式图形的识图训练,培养学生的识图能力;通过例题口答“为什么”,培养学生的推理能力;从复杂图形分解为基本图形的过程中,渗透化繁为简,化难为易的化归思想;从图形变化过程中,培养学生辩证唯物主义观点;通过“三线八角”基本图形,使学生认识几何图形的位置美.
三、教学问题诊断分析
七年级学生对几何图形的认识有浓厚的兴趣,但相对掌握的几何知识还是较浅显的.特别是“图形、符合、文字”三种语言之间的相互转化.因此,本节课我重点以概念教学为主.通过学生看书、思考、组内交流、汇报、教师评价等形式得出“同位角、内错角、同旁内角”的概念.然后再通过达标练习进行反馈,在反馈中补充和升华,真正使学生达到理解、掌握的目的,从而为后续学习内容做铺垫.
基于以上学情分析,确定本节课的教学难点为:从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.
四、教学过程设计
自学导航
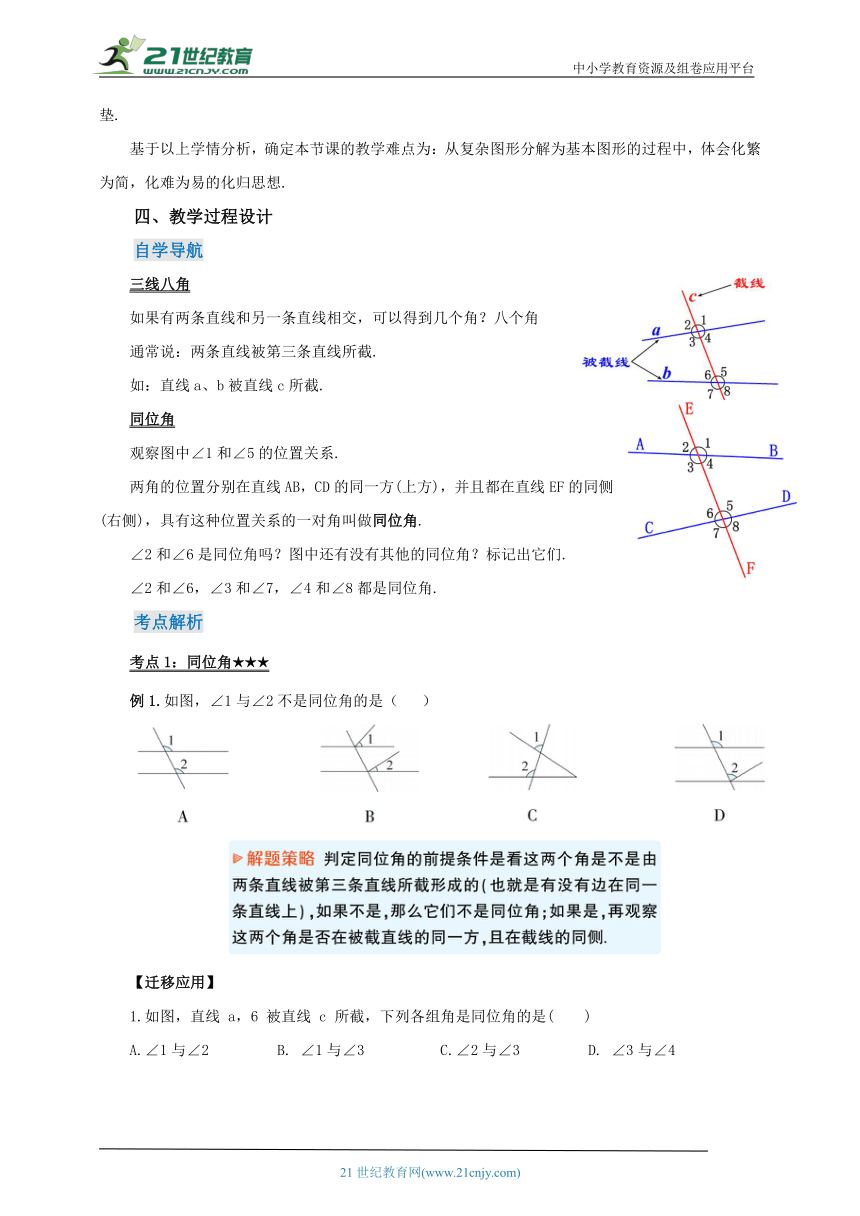
三线八角
如果有两条直线和另一条直线相交,可以得到几个角?八个角
通常说:两条直线被第三条直线所截.
如:直线a、b被直线c所截.
同位角
观察图中∠1和∠5的位置关系.
两角的位置分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做同位角.
∠2和∠6是同位角吗?图中还有没有其他的同位角?标记出它们.
∠2和∠6,∠3和∠7,∠4和∠8都是同位角.
考点解析
考点1:同位角★★★
例1.如图,∠1与∠2不是同位角的是( )
【迁移应用】
1.如图,直线 a,6 被直线 c 所截,下列各组角是同位角的是( )
A.∠1与∠2 B. ∠1与∠3 C.∠2与∠3 D. ∠3与∠4
2.如图,与∠1是同位角的是( )
A.∠2 B. ∠3 C.∠4 D. ∠5
3.如图_______和∠C是直线 BE,CD被直线_____所截形成的同位角,_______和∠C是直线_____,_____被直线AC所截形成的同位角.
自学导航
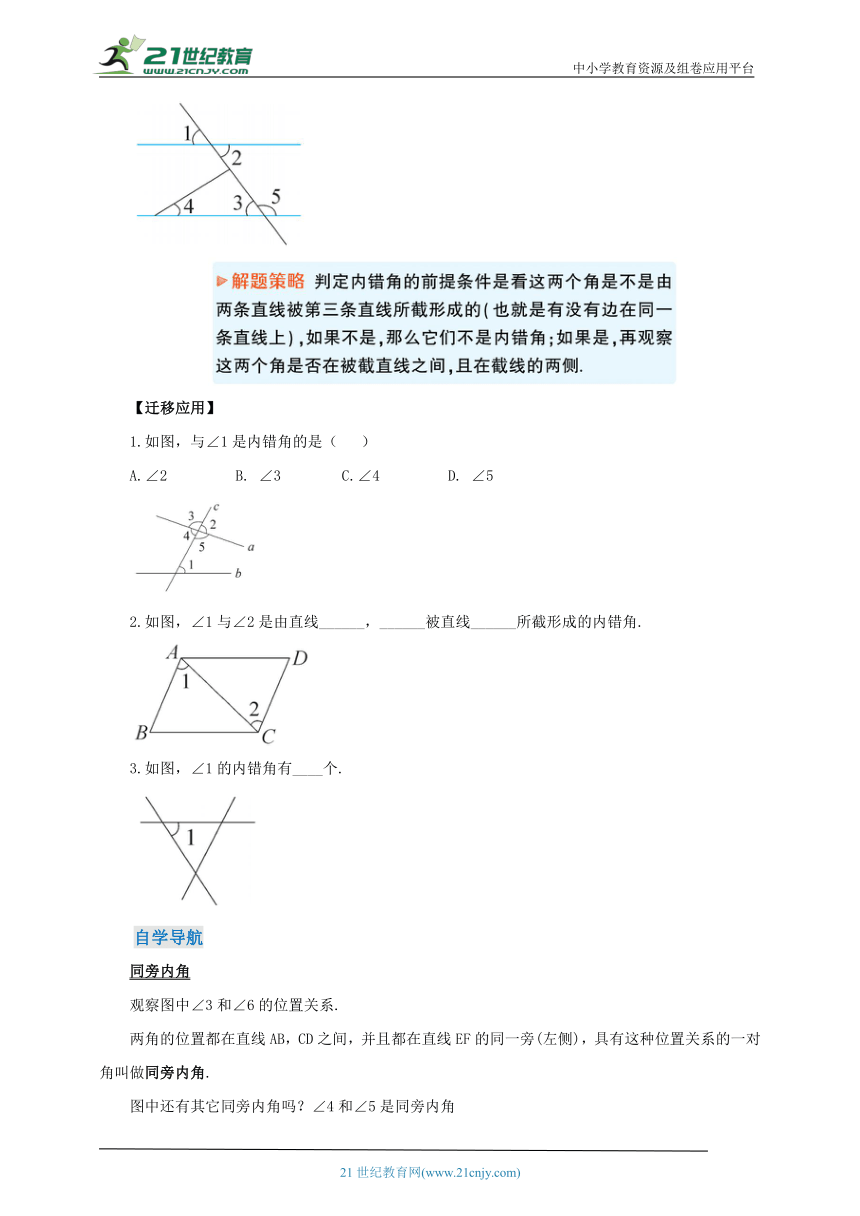
内错角
观察图中∠3和∠5的位置关系.
两角的位置都在直线AB,CD之间,并且分别在直线EF两侧(∠3在直线EF左侧,∠5在直线EF右侧),具有这种位置关系的一对角叫做内错角.
图中还有其它内错角吗?∠4和∠6是内错角
考点解析
考点2:内错角★★★
例2.如图下列各组角中,是内错角的是( )
A.∠1和∠2 B. ∠2和∠3 C.∠1和∠3 D. ∠2和∠5
【迁移应用】
1.如图,与∠1是内错角的是( )
A.∠2 B. ∠3 C.∠4 D. ∠5
2.如图,∠1与∠2是由直线______,______被直线______所截形成的内错角.
3.如图,∠1的内错角有____个.
自学导航
同旁内角
观察图中∠3和∠6的位置关系.
两角的位置都在直线AB,CD之间,并且都在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角.
图中还有其它同旁内角吗?∠4和∠5是同旁内角
考点解析
考点3:同旁内角★★★
例3.如图,∠C与哪个角是同旁内角
解:∠C与∠EDC,∠DFC,∠ADC,∠ABC是同旁内角.
【迁移应用】
1.如图,下列两个角是同旁内角的是( )
A.∠1与∠2 B. ∠1与∠3 C.∠1与∠4 D. ∠2与∠4
2.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角.其中正确的是________.( 填序号)
3.如图,如果∠1=40°,∠2= 100°,那么∠3的同位角等于______,∠3的内错角等于______,∠3的同旁内角等于______.
4.如图,∠D与哪个角是同旁内角
解:∠D与∠C,∠CED,∠BED是同旁内角.
自学导航
同位角、内错角、同旁内角的结构特征:
注:上述三类角类似于对顶角都是成对出现. 不能说哪个角是同位角、内错角、同旁内角.
考点解析
考点4:识别“三线八角”★★★★
例4.如图,在∠1,∠2,∠3,∠4,∠5和∠B中,______是同位角,_____是内错角,______是同旁内角.
解析:为了能正确地识别且防止遗漏,可以把图形分解成基本图形,如图①②③.
【迁移应用】
1.指出图中各对角的位置关系:
(1)∠C和∠D是________角;
(2)∠B和∠GEF是______角;
(3)∠A和∠D是_______角;
(4)∠AGE和∠BGE是_______角;
(5)∠CFD和∠AFB是_______角.
2.如图,下列说法不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3与∠4是内错角 D.∠3与∠5是同旁内角
3.如图,在∠1,∠2,∠3,∠4,∠5中,同位角、内错角、同旁内角的对数分别是( )
A.1,1,4 B.1,2,4 C.2,1,4 D.1,1,5
考点5:通过同位角、内错角、同旁内角辨别截线、被截直线★★★★
例5.填空:
(1)如图①,∠1和∠ABC是直线______,______被直线______所截形成的_______角;
(2)如图②,∠EDC和_______是直线DE,BC被直线______所截形成的内错角;
(3)如图①,如果∠1=∠ABC,那么∠ABC与∠BCF相等吗 ∠ABC与∠BCE互补吗 为什么
(3)如果∠1=∠ABC,由对顶角相等,得∠1=∠BCF,那么∠ABC=∠BCF.
因为∠1和∠BCE互补,所以∠1+∠BCE= 180°.
又∠1=∠ABC,所以∠ABC+∠BCE= 180°,
所以∠ABC与∠BCE互补.
【迁移应用】
1.如图,根据图形填空:
(1)∠FAD和∠____是_____与_____被_____所截形成的同位角;
(2)∠FAC和∠____是_____与_____被_____所截形成的同位角;
(3)∠CAD和∠______是_____与_____被_____所截形成的内错角;
(4)∠FAC和∠______是_____与_____被______所截形成的内错角;
(5)∠BAD和∠______是_____与_____被______所截形成的同旁内角;
(6)∠CAD和∠______是_____与_____被______所截形成的同旁内角.
2. 下列各图中,∠1和∠2,∠3和∠4分别是哪两条直线被哪一条直线所截形成的 它们各是什么角
解:图①中的∠1和∠2是直线AB,DC被直线DB所截形成的,它们是内错角;∠3和∠4是直线AD,BC被直线DB所截形成的,它们是内错角.
图②中的∠1和∠2是直线AB,DC被直线BC所截形成的,它们是同位角;∠3和∠4是直线AB,BC被直线AC所截形成的,它们是同旁内角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1.3 同位角、内错角、同旁内角 教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第五章“相交线与平行线”5.1.3 同位角、内错角、同旁内角,内容包括:同位角、内错角、同旁内角的概念及辨识.
2.内容解析
本节内容主要是学习同位角、内错角、同旁内角的概念,在研究了两条相交直线构成的角(对顶角,邻补角)的基础上进一步探究平面内三条直线相交形成的不共顶点的角的位置关系,主要学习同位角、内错角、同旁内角的概念.它是进一步学习平行线的判定和性质的必要准备.
教科书通过两条直线相交的四个角的知识为基础,引出一条直线分别与两条直线相交构成的八个角中,通过分类讨论思想,把不共顶点的两个角的位置关系分为同位角、内错角、同旁内角三类.紧接着,通过一个例题来让学生学习同位角、内错角、同旁内角的概念,教学时可根据情况适当要求学生说明同位角、内错角与同旁内角是哪两条直线被哪一条直线所截得到的,为后面学习平行线的性质与判定做好铺垫.
基于以上分析,确定本节课的教学重点为:理解同位角、内错角、同旁内角的概念.
二、目标和目标解析
1.目标
(1)理解同位角、内错角、同旁内角的概念;
(2)结合图形识别同位角、内错角、同旁内角;
(3)从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.
2.目标解析
理解同位角、内错角、同旁内角的概念结合图形识别同位角、内错角、同旁内角;通过变式图形的识图训练,培养学生的识图能力;通过例题口答“为什么”,培养学生的推理能力;从复杂图形分解为基本图形的过程中,渗透化繁为简,化难为易的化归思想;从图形变化过程中,培养学生辩证唯物主义观点;通过“三线八角”基本图形,使学生认识几何图形的位置美.
三、教学问题诊断分析
七年级学生对几何图形的认识有浓厚的兴趣,但相对掌握的几何知识还是较浅显的.特别是“图形、符合、文字”三种语言之间的相互转化.因此,本节课我重点以概念教学为主.通过学生看书、思考、组内交流、汇报、教师评价等形式得出“同位角、内错角、同旁内角”的概念.然后再通过达标练习进行反馈,在反馈中补充和升华,真正使学生达到理解、掌握的目的,从而为后续学习内容做铺垫.
基于以上学情分析,确定本节课的教学难点为:从复杂图形分解为基本图形的过程中,体会化繁为简,化难为易的化归思想.
四、教学过程设计
自学导航
三线八角
如果有两条直线和另一条直线相交,可以得到几个角?八个角
通常说:两条直线被第三条直线所截.
如:直线a、b被直线c所截.
同位角
观察图中∠1和∠5的位置关系.
两角的位置分别在直线AB,CD的同一方(上方),并且都在直线EF的同侧(右侧),具有这种位置关系的一对角叫做同位角.
∠2和∠6是同位角吗?图中还有没有其他的同位角?标记出它们.
∠2和∠6,∠3和∠7,∠4和∠8都是同位角.
考点解析
考点1:同位角★★★
例1.如图,∠1与∠2不是同位角的是( )
【迁移应用】
1.如图,直线 a,6 被直线 c 所截,下列各组角是同位角的是( )
A.∠1与∠2 B. ∠1与∠3 C.∠2与∠3 D. ∠3与∠4
2.如图,与∠1是同位角的是( )
A.∠2 B. ∠3 C.∠4 D. ∠5
3.如图_______和∠C是直线 BE,CD被直线_____所截形成的同位角,_______和∠C是直线_____,_____被直线AC所截形成的同位角.
自学导航
内错角
观察图中∠3和∠5的位置关系.
两角的位置都在直线AB,CD之间,并且分别在直线EF两侧(∠3在直线EF左侧,∠5在直线EF右侧),具有这种位置关系的一对角叫做内错角.
图中还有其它内错角吗?∠4和∠6是内错角
考点解析
考点2:内错角★★★
例2.如图下列各组角中,是内错角的是( )
A.∠1和∠2 B. ∠2和∠3 C.∠1和∠3 D. ∠2和∠5
【迁移应用】
1.如图,与∠1是内错角的是( )
A.∠2 B. ∠3 C.∠4 D. ∠5
2.如图,∠1与∠2是由直线______,______被直线______所截形成的内错角.
3.如图,∠1的内错角有____个.
自学导航
同旁内角
观察图中∠3和∠6的位置关系.
两角的位置都在直线AB,CD之间,并且都在直线EF的同一旁(左侧),具有这种位置关系的一对角叫做同旁内角.
图中还有其它同旁内角吗?∠4和∠5是同旁内角
考点解析
考点3:同旁内角★★★
例3.如图,∠C与哪个角是同旁内角
解:∠C与∠EDC,∠DFC,∠ADC,∠ABC是同旁内角.
【迁移应用】
1.如图,下列两个角是同旁内角的是( )
A.∠1与∠2 B. ∠1与∠3 C.∠1与∠4 D. ∠2与∠4
2.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角.其中正确的是________.( 填序号)
3.如图,如果∠1=40°,∠2= 100°,那么∠3的同位角等于______,∠3的内错角等于______,∠3的同旁内角等于______.
4.如图,∠D与哪个角是同旁内角
解:∠D与∠C,∠CED,∠BED是同旁内角.
自学导航
同位角、内错角、同旁内角的结构特征:
注:上述三类角类似于对顶角都是成对出现. 不能说哪个角是同位角、内错角、同旁内角.
考点解析
考点4:识别“三线八角”★★★★
例4.如图,在∠1,∠2,∠3,∠4,∠5和∠B中,______是同位角,_____是内错角,______是同旁内角.
解析:为了能正确地识别且防止遗漏,可以把图形分解成基本图形,如图①②③.
【迁移应用】
1.指出图中各对角的位置关系:
(1)∠C和∠D是________角;
(2)∠B和∠GEF是______角;
(3)∠A和∠D是_______角;
(4)∠AGE和∠BGE是_______角;
(5)∠CFD和∠AFB是_______角.
2.如图,下列说法不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3与∠4是内错角 D.∠3与∠5是同旁内角
3.如图,在∠1,∠2,∠3,∠4,∠5中,同位角、内错角、同旁内角的对数分别是( )
A.1,1,4 B.1,2,4 C.2,1,4 D.1,1,5
考点5:通过同位角、内错角、同旁内角辨别截线、被截直线★★★★
例5.填空:
(1)如图①,∠1和∠ABC是直线______,______被直线______所截形成的_______角;
(2)如图②,∠EDC和_______是直线DE,BC被直线______所截形成的内错角;
(3)如图①,如果∠1=∠ABC,那么∠ABC与∠BCF相等吗 ∠ABC与∠BCE互补吗 为什么
(3)如果∠1=∠ABC,由对顶角相等,得∠1=∠BCF,那么∠ABC=∠BCF.
因为∠1和∠BCE互补,所以∠1+∠BCE= 180°.
又∠1=∠ABC,所以∠ABC+∠BCE= 180°,
所以∠ABC与∠BCE互补.
【迁移应用】
1.如图,根据图形填空:
(1)∠FAD和∠____是_____与_____被_____所截形成的同位角;
(2)∠FAC和∠____是_____与_____被_____所截形成的同位角;
(3)∠CAD和∠______是_____与_____被_____所截形成的内错角;
(4)∠FAC和∠______是_____与_____被______所截形成的内错角;
(5)∠BAD和∠______是_____与_____被______所截形成的同旁内角;
(6)∠CAD和∠______是_____与_____被______所截形成的同旁内角.
2. 下列各图中,∠1和∠2,∠3和∠4分别是哪两条直线被哪一条直线所截形成的 它们各是什么角
解:图①中的∠1和∠2是直线AB,DC被直线DB所截形成的,它们是内错角;∠3和∠4是直线AD,BC被直线DB所截形成的,它们是内错角.
图②中的∠1和∠2是直线AB,DC被直线BC所截形成的,它们是同位角;∠3和∠4是直线AB,BC被直线AC所截形成的,它们是同旁内角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
